初中数学北师大版（2024）九年级上册第一章 特殊平行四边形3 正方形的性质与判定优秀课后测评

这是一份初中数学北师大版（2024）九年级上册第一章 特殊平行四边形3 正方形的性质与判定优秀课后测评，文件包含专题15特殊四边形中的折叠问题的四大题型北师大版原卷版docx、专题15特殊四边形中的折叠问题的四大题型北师大版解析版docx等2份试卷配套教学资源，其中试卷共86页， 欢迎下载使用。

考卷信息：
本套训练卷共30题，题型针对性较高，覆盖面广，选题有深度，可加强学生对特殊四边形中的折叠问题的四大题型的理解！
【题型1 矩形中的折叠问题】
1．（2023春·吉林长春·九年级统考期末）综合与实践
【操作感知】如图①，在矩形纸片ABCD的AD边上取一点P，沿BP折叠，使点A落在矩形内部点M处，把纸片展平，连接PM、BM．∠DPM=60°，则∠MBC的大小为 度．
【迁移探究】如图②，将矩形纸片换成正方形纸片，将正方形纸片ABCD按照【操作感知】进行折叠，并延长PM交CD于点Q，连接BQ．
（1）判断△MBQ与△CBQ的关系并证明．
（2）若正方形ABCD的边长为4，点P为AD中点，则CQ的长为 ．
2．（2023春·山东临沂·九年级统考期末）已知长方形ABCD(对边平行且相等，四个角都是直角)中，AB=6，AD=8，点P在边BC上，且不与点B、C重合，直线AP与DC的延长线交于点E．

(1)如图1，当点P是BC的中点时，求证：△ABP≌△ECP；
(2)如图2，将△APB沿直线AP折叠得到△APB′，点B′落在长方形ABCD的内部，延长P B′交直线AD于点F．
①证明FA=FP，并求出在1条件下AF的值；
②连接B′C，求△PCB′周长的最小值．
3．（2023春·湖南岳阳·九年级校考期中）如图，将矩形纸片ABCDAD>AB折叠，使点C刚好落在线段AD上，且折痕分别与边BC、AD相交，设折叠后点C、D的对应点分别为点G、H，折痕分别与边BC、AD相交于点E、F．

(1)判断四边形CEGF的形状，并证明你的结论．
(2)若CD=2，GD=16，求DF的长．
4．（2023春·江苏南京·九年级校联考期末）数学课上老师让学生们折矩形纸片．由于折痕所在的直线不同，折出的图形也不同，所以各个图形中所隐含的“基本图形”也不同．我们可以通过发现基本图形，来研究这些图形中的几何问题．

问题解决：
（1）如图1，将矩形纸片ABCD沿直线MN折叠，使得点C与点A重合，点D落在点D1的位置，连接MC，AN，AC，线段AC交MN于点O，则：
①△CDM与△AD1M的关系为 ，线段AC与线段MN的关系为 ，小强量得∠MNC=50°，则∠DAN= ．
②小丽说：“图1中的四边形ANCM是菱形”，请你帮她证明．
拓展延伸：
（2）如图2，矩形纸片ABCD中，BC=2AB=6cm，BM=4cm，小明将矩形纸片ABCD沿直线AM折叠，点B落在点B1的位置，MB1交AD于点N，请你直接写出线段ND的长： ．
综合探究：
（3）如图3，ABCD是一张矩形纸片，AD=1，AB=5，在矩形ABCD的边AB上取一点M（不与A和B点重合），在边CD上取一点N（不与C和D点重合），将纸片沿MN折叠，使线段MB与线段DN交于点P，得到△MNP，请你确定△MNP面积的取值范围 ．
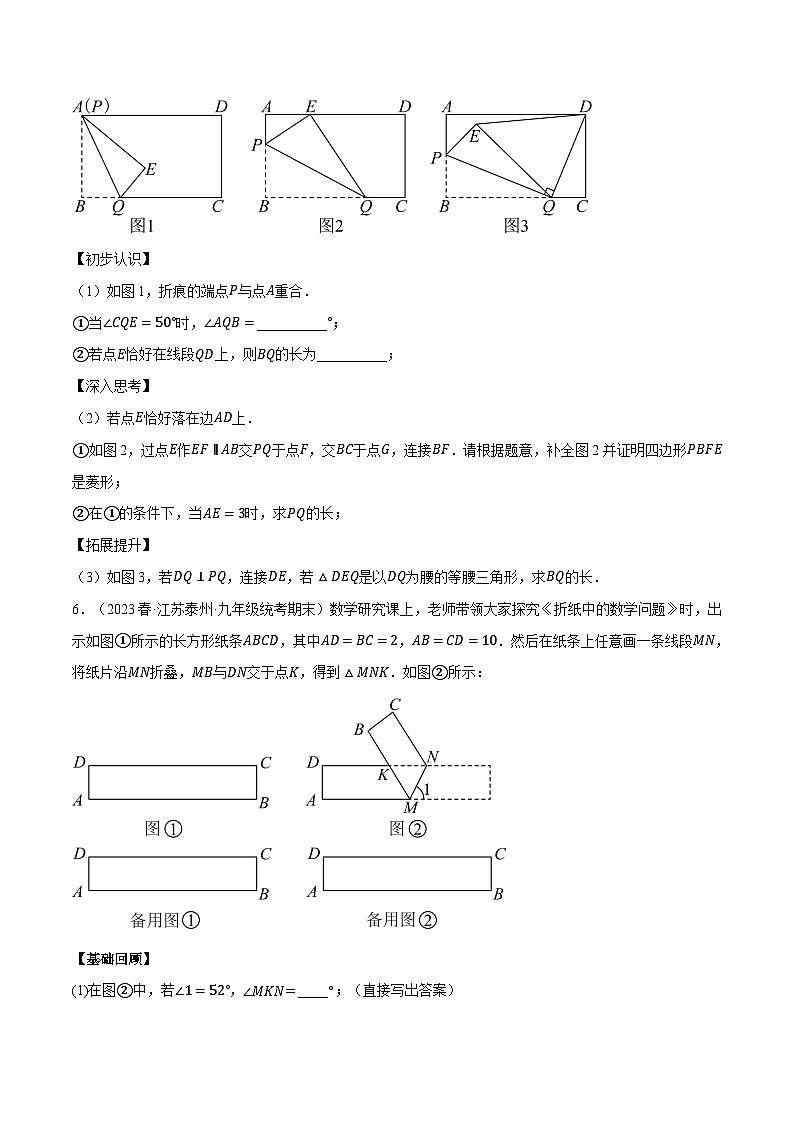
5．（2023春·江苏连云港·九年级统考期末）【问题背景】矩形纸片ABCD中，AB=6，BC=10，点P在AB边上，点Q在BC边上，将纸片沿PQ折叠，使顶点B落在点E处．

【初步认识】
（1）如图1，折痕的端点P与点A重合．
①当∠CQE=50°时，∠AQB=__________°；
②若点E恰好在线段QD上，则BQ的长为__________；
【深入思考】
（2）若点E恰好落在边AD上．
①如图2，过点E作EF∥AB交PQ于点F，交BC于点G，连接BF．请根据题意，补全图2并证明四边形PBFE是菱形；
②在①的条件下，当AE=3时，求PQ的长；
【拓展提升】
（3）如图3，若DQ⊥PQ，连接DE，若△DEQ是以DQ为腰的等腰三角形，求BQ的长．
6．（2023春·江苏泰州·九年级统考期末）数学研究课上，老师带领大家探究《折纸中的数学问题》时，出示如图①所示的长方形纸条ABCD，其中AD=BC=2，AB=CD=10．然后在纸条上任意画一条线段MN，将纸片沿MN折叠，MB与DN交于点K，得到△MNK．如图②所示：

【基础回顾】
(1)在图②中，若∠1=52°，∠MKN＝______°；（直接写出答案）
【操作探究】
(2)改变折痕MN位置，△MNK始终是______三角形，请说明理由；
(3)爱动脑筋的小明在研究△MNK的面积时，发现KN边上的高始终是个不变的值．根据这一发现，他很快研究出△KMN的面积最小值为2，此时∠1的大小可以为______；
【拓展延伸】
(4)小明继续动手操作进行折纸，发现了△MNK面积存在最大值，请你求出这个最大值．
7．（2023春·河南洛阳·九年级统考期末）小明尝试着将矩形纸片ABCD（如图1，AD>CD）沿过点A的直线折叠，使得点B落在AD边上的点F处，折痕为AE（如图2）；再沿过点D的直线折叠，使得点C落在AD边上的点N处，点E落在AE上的点M处，折痕为DG（如图3）．若第二次折叠后，点M正好在∠NDG的平分线上，连接DM，且CD=1，则AD＝ ．

8．（2023春·浙江杭州·九年级统考期末）如图是一张矩形纸片ABCD，点E在边BC上，且满足 AB=2BE，把△ABE沿直线AE折叠，使点B落在点F处，EF的延长线与边CD交于点G．若CG=DG，则CEBE= ．

【题型2 菱形中的折叠问题】
1．（2023春·安徽淮南·九年级统考期末）如图，在菱形ABCD中，BC=4，∠B=120°，点E是AD的中点，点F是AB上一点，以EF为对称轴将△EAF折叠得到△EGF，以CE为对称轴将△CDE折叠得到△CHE，使得点H落到EG上，连接AG．下列结论错误的是（ ）

A．∠CEF=90°B．CE∥AGC．FG=1.6D．CFAB=145
2．（2023春·安徽安庆·九年级统考期末）如图，在菱形ABCD中，∠A=120°，AB=2，点E是边AB上一点，以DE为对称轴将△DAE折叠得到△DGE，再折叠BE使BE落在直线EG上，点B的对应点为点H，折痕为EF且交BC于点F．

（1）∠DEF= ；
（2）若点E是AB的中点，则DF的长为 ．
3．（2023秋·河南开封·九年级开封市第十三中学校考期末）如图，在菱形ABCD中，∠B=60°，AB=4，M为边AB的中点，N为边BC上一动点（不与点B重合），将△BMN沿直线MN折叠，使点B落在点E 处，连接DE，CE，当△CDE为等腰三角形时，BN的长为 ．

4．（2023春·重庆沙坪坝·九年级重庆南开中学校考期末）如图，在菱形ABCD中，对角线AC、BD交于点O，AC=6，菱形ABCD的面积为24，点E是边AB上一点，将菱形ABCD沿DE折叠，使B、C的对应点分别是B′、C′，若∠BEB′=90°，则点C′到BC的距离为 ．

5．（2023春·广西来宾·九年级校考期末）如图，在菱形ABCD中，∠ABC=120°，将菱形折叠，使点A恰好落在对角线BD上的点G处（不与B、D重合），折痕为EF，若DG=2，AD=6，则BE的长为 ．

6．（2023春·浙江杭州·九年级统考期末）如图，菱形ABCD中，AB=2，M为边AB上的一点，将菱形沿DM折叠后，点A恰好落在BC的中点E处，则AM= ．

7．（2023春·广东肇庆·九年级统考期末）如图1，菱形纸片ABCD的边长为6cm，∠ABC=60°，将菱形ABCD沿EF，GH折叠，使得点B，D两点重合于对角线BD上的点P（如图2）．若AE=2BE，则六边形AEFCHG的面积为 cm2．

【题型3 正方形中的折叠问题】
1．（2023春·陕西西安·九年级校考期末）在正方形ABCD中，点G是边DC上的一点，点F是直线BC上一动点，FE⊥AG于H，交直线AD于点E．
（1）当点F运动到与点B重合时(如图1)，线段EF与AG的数量关系是________．
（2）若点F运动到如图2所示的位置时，（1）探究的结论还成立吗？如果成立，请给出证明：如果不成立，请说明理由．
（3）如图3，将边长为6的正方形ABCD折叠，使得点A落在边CD的中点M处，折痕为PQ，点P、Q分别在边AD、BC上，请直接写出折痕PQ的长．
2．（2023春·山西大同·九年级校联考期中）综合与实践
问题情境：
在数学综合与实践活动课上，老师以“正方形的折叠问题”为主题开展数学活动.如图1，将正方形纸片ABCD对折，使得边AB与CD重合，展开铺平，折痕为PQ.然后，再将正方形纸片沿着过点C的直线折叠，此时点B恰好落在折痕PQ的点F处，展开铺平，设CE与PQ交于点G，连接BG，得到图2.

(1)操作发现：小康发现，四边形BGFE是菱形，请说明理由；
(2)问题解决：若正方形ABCD的边长为6，求FQ的长；
(3)问题拓展：如图3，M是正方形ABCD的边AD上一点，正方形ABCD的边长为8，连接BM，将△ABM沿着BM折叠，使得点A落在正方形ABCD的内部点K处，连接DK，求出DK的最小值.
3．（2023春·江苏泰州·九年级统考期末）【模型建立】
如图1，正方形ABCD中，点E，F分别在边BC，CD上，AE⊥BF，AE与BF相交于点P．AE，BF有什么数量关系?请说明理由．

【迁移应用】
如图2，请仅用无刻度的直尺画图（保留作图痕迹，不用证明）
（1）以AB为边画正方形ABCD；
（2）取CD中点E，连接AE：
（3）在AD上找点G，连接BG，使BG=AE．

【拓展提升】
如图3，正方形ABCD中，点E，F分别在边AB，CD上，将正方形沿EF折叠，点A，D的对应点分别为A′，D′，使得点A′始终落在边BC上，A′D与CD相交于点G．
（1）若AB=5，BA′=2，求DF的长度；
（2）点E，F在边AB，CD上运动时，连接AG，则∠A′AG的大小是否发生改变，若不变，求出大小，若改变，请说明理由．

4．（2023春·河南南阳·九年级统考期末）动手操作：利用“正方形纸片的折叠”开展数学活动，探究在正方形折叠的过程中图形的变化及其蕴含的数学思想方法．

折一折：如图1，已知正方形ABCD的边长AB=6，将正方形ABCD沿过点A的直线折叠，使点B的对应点M落在AC上，展开正方形ABCD，折痕为AE，延长EM交CD于点F，连接AF．
思考探究：（1）图1中，与△ABE全等的三角形有________个，∠EAF=________，BE、EF、DF三者的数量关系是________．
转一转：将图1中的∠EAF绕点A旋转到图2所示位置，与BC、CD的交点分别为E、F，连接EF．
证明推理：（2）图2中，BE、EF、DF三者的数量关系是________，并给出证明．
开放拓展：（3）如图3，在旋转∠EAF的过程中，当点F为CD的中点时，BE的长为________．
5．（2023春·江苏南京·九年级校联考期中）点 E．F 分别为正方形 ABCD 边 AD．AB 上的点，连接 CE，DF 交于点 P．
(1)如图 1，若 DE=AF，则线段 DF 与 CE 具有怎样的数量和位置关系？说明理由．
(2)如图 2，若 E 为 AD 中点，F 为 AB 中点，求证 BP=BC．
(3)若将正方形 ABCD 折叠，使得 A 点的对应点 A'落在 BC 边上，折痕 MN 分别交 AB，CD 于 M，N．若正方形的的边长为 6，线段 A'B=2，则 DN 的长为 ．
6．（2023春·广东江门·九年级统考期末）综合与实践：
如图1，已知正方形纸片ABCD．
实践操作
第一步：如图1，将正方形纸片ABCD沿AC，BD分别折叠．然后展平，得到折痕AC，BD．折痕AC，BD相交于点O．
第二步：如图2，将正方形ABCD折叠，使点B的对应点E恰好落在AC上，得到折痕AF，AF与BD相交于点G，然后展平，连接GE，EF．
问题解决
（1）∠AGD的度数是______；
（2）如图2，请判断四边形BGEF的形状，并说明理由；
探索发现
（3）如图3，若AB=1，将正方形ABCD折叠，使点A和点F重合，折痕分别与AB，DC相交于点M，N．求MN2的值．
7．（2023春·海南省直辖县级单位·九年级统考期末）已知正方形ABCD的边长AB=6，将正方形ABCD沿过点A的直线折叠，使点B的对应点M落在AC上，展开正方形ABCD，折痕为AE，延长EM交CD于点F，连接AF．则∠EAF= °，BE的长为 ．

【题型4 坐标系中的折叠问题】
1．（2023春·黑龙江齐齐哈尔·九年级统考期中）综合与探究
如图，在平面直角坐标系中，点A、C的坐标分别为0,a和b,0，且a，b满足b=a−8+8−a+4．将矩形OABC沿对角线AC所在的直线折叠，点B落在点D处，DC与y轴相交于点E．

(1)a=___________，b=___________；
(2)试证明△ADE≌△COE，并直接写出点E的坐标；
(3)若点F是线段AC上的一个动点，则EF+OF的最小值为___________；
(4)平面内是否存在点M与点N使四边形ACMN为正方形？若存在，请直接写出点M的坐标；若不存在，请说明理由．
2．（2017春·北京丰台·九年级统考期中）已知菱形OABC在坐标系中的位置如图所示，O是坐标原点，点C(1,2)，点A在x轴上，点M(0，2)．
(1)点P是直线OB上的动点，求PM+PC最小值.
(2)将直线y=−x−1向上平移，得到直线y=kx+b.
①当直线y=kx+b与线段OC有公共点时，结合图像，直接写出b的取值范围.
②当直线y=kx+b将四边形OABC分成面积相等的两部分时，求k，b．
（只需写出解题的主要思路，不用写出计算结果）.
3．（2023春·福建泉州·九年级统考期末）如图，四边形OABC为矩形，其中O为原点，A、C两点分别在x轴和y轴上，B点的坐标是（4，7）．点D，E分别在OC，CB边上，且CE：EB＝5：3．将矩形OABC沿直线DE折叠，使点C落在AB边上点F处．
（1）求F点的坐标；
（2）点P在第二象限，若四边形PEFD是矩形，求P点的坐标；
（3）若M是坐标系内的点，点N在y轴上，若以点M，N，D，F为顶点的四边形是菱形，请直接写出所有满足条件的点M和点N的坐标．
4．（2023春·天津南开·九年级统考期末）将一个矩形纸片OABC放置于平面直角坐标系中，点O0,0，点B10,6，点A在x轴，点C在y轴．在AB边上取一点D，将△CBD沿CD翻折，点B恰好落在边OA上的点E处．

(1)如图1，求点E坐标和直线CE的解析式；
(2)点P为x轴正半轴上的动点，设OP=t．
①如图2，当点P在线段OA（不包含端点A，O）上运动时，过点P作直线l∥y轴，直线l被△CED截得的线段长为d．求d关于t的函数关系式，并直接写出自变量t的取值范围；
②在该坐标系所在平面内找一点G，使以点C，E，P，G为顶点的四边形为菱形，请直接写出点G的坐标．
5．（2023春·广东惠州·九年级统考期末）如图，矩形OABC的顶点A、C分别位于x轴和y轴的正半轴上，线段OA、OC的长度满足：OA−15+OC−9=0，点N在OC上，将△BCN沿直线BN折叠，点C恰好落在x轴上的点D处，且OD=3．

(1)求点B的坐标；
(2)求直线BN的解析式；
(3)坐标平面内是否存在一点P，使以B、N，D、P为顶点的四边形是平行四边形？若存在，请说明理由并求出点P的坐标；若不存在，请说明理由．
6．（2023春·陕西西安·九年级西安市曲江第一中学校考期末）如图1，在矩形ABCD中，将矩形折叠，使点B落在边AD（含端点）上，落点记为E．这时折痕与边BC或者边CD（含端点）交于点F，然后展开铺平，则以B、E、F为顶点的△BEF称为矩形ABCD的“折痕三角形”．

(1)由“折痕三角形”的定义可知，矩形ABCD的任意一个“折痕△BEF”一定是______三角形．
(2)如图2，在矩形ABCD中，AB=2,BC=4．当点F与点C重合，画出这个“折痕△BEF”，并求出点E的坐标．
(3)如图3，在矩形ABCD中，AB=2,BC=4，当“折痕△BEF”面积最大的时，求出此时点F的坐标．
7．（2023春·湖北武汉·九年级统考期中）在平面直角坐标系中，四边形OABC为矩形，Aa,0，C0,c，且10−a+c−82=0．点E从B点出发沿BC运动，点F从B点出发沿BA运动，点G从O点出发沿OC运动．
(1)直接写出a，c的值；
(2)如图1，将△AOF沿OF折叠，点A恰好落在点E处，求E，F两点的坐标；
(3)如图2，若E，F两点以相同的速度同时出发运动，使∠EOF=45°，设点E的横坐标为m，求m2+16m的值；
(4)如图3，已知点D7.5,0，若F，G两点以相同的速度同时出发运动，连接FG，作AH⊥FG于H，直接写出DH的最大值．
8．（2023秋·四川达州·九年级校考期中）如图，在平面直角坐标系中，四边形OABC是长方形，O为坐标原点，顶点A，C分别在y轴、x轴上，顶点B在第二象限内，一次函数y=34x+6的图象分别与坐标轴交于点A，C．
(1)如图①，将△ABC折叠使得点C落在长方形的边AB上的点E处，折痕为BD，求点B，E的坐标；
(2)如图②，将△ABC折叠使得点B落在对角线AC上的点E处，折痕为AD，求点D的坐标；
(3)在平面直角坐标系内，是否存在一点E(除点B外），使得△AEC与△ABC全等？若存在，写出所有符合条件的点E的纵坐标；若不存在，请说明理由．