北师大版（2024）九年级上册1 反比例函数优秀测试题

这是一份北师大版（2024）九年级上册1 反比例函数优秀测试题，文件包含专题64反比例函数中k的几何意义与面积之间关系探究六大题型北师大版原卷版docx、专题64反比例函数中k的几何意义与面积之间关系探究六大题型北师大版解析版docx等2份试卷配套教学资源，其中试卷共65页， 欢迎下载使用。

考卷信息：
本套训练卷共40题，题型针对性较高，覆盖面广，选题有深度，可加强学生对反比例函数中k的几何意义与面积之间关系探究六大题型的理解！
【题型1 根据k的几何意义求三角形的面积】
1．（2023春·上海·九年级期中）如图，△OAC和△BAD都是等腰直角三角形，∠ACO＝∠ADB＝90°，反比例函数y＝6x在第一象限的图象经过点B，则△OAC与△BAD的面积之差即S△OAC－ S△BAD等于( )
A．3B．6C．4D．9
2．（2023春·山东烟台·九年级统考期中）如图，在平面直角坐标系中，点A、B、C为反比例函数y=kx(k>0)上不同的三点，连接，OA、OB、OC，过点A作AD⊥x轴于点D，过点B、C分别作BE，CF垂直y轴于点E、F，OB与CF相交于点G，记四边形BEFG、△COG、△AOD的面积分别为S1、S2、S3，则( )
A．S1>S2>S3B．S3S1
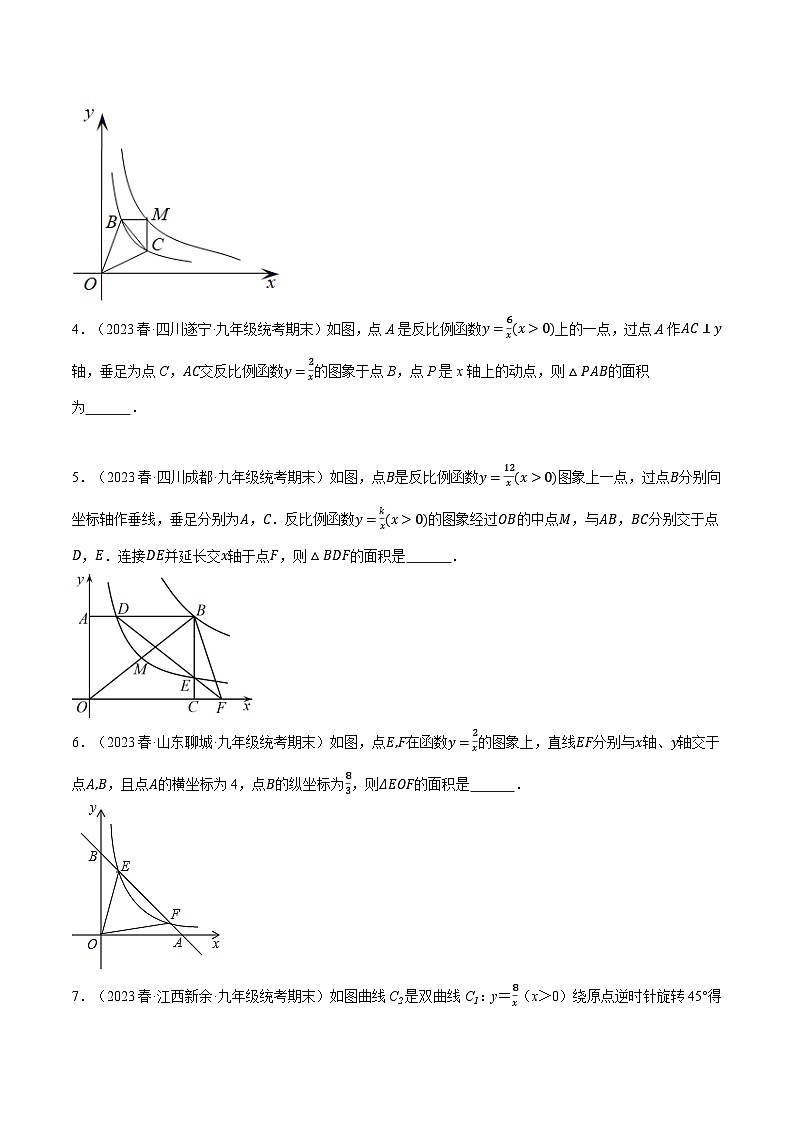
3．（2023春·江苏·九年级期末）如图，点M在函数y=5x（x＞0）的图像上，过点M分别作x轴和y轴的平行线交函数y=2x（x＞0）的图像于点B、C，连接OB、OC，则△OBC的面积为 ．
4．（2023春·四川遂宁·九年级统考期末）如图，点A是反比例函数y=6x(x>0)上的一点，过点A作AC⊥y轴，垂足为点C，AC交反比例函数y=2x的图象于点B，点P是x轴上的动点，则△PAB的面积为 ．
5．（2023春·四川成都·九年级统考期末）如图，点B是反比例函数y=12x(x>0)图象上一点，过点B分别向坐标轴作垂线，垂足分别为A，C．反比例函数y=kx(x>0)的图象经过OB的中点M，与AB，BC分别交于点D，E．连接DE并延长交x轴于点F，则△BDF的面积是 ．
6．（2023春·山东聊城·九年级统考期末）如图，点E,F在函数y=2x的图象上，直线EF分别与x轴、y轴交于点A,B，且点A的横坐标为4，点B的纵坐标为83，则ΔEOF的面积是 ．
7．（2023春·江西新余·九年级统考期末）如图曲线C2是双曲线C1：y＝8x（x＞0）绕原点逆时针旋转45°得到的图形，P是曲线C2上任意一点，点A在直线l：y＝x上，且PA＝PO，则△POA的面积等于 ．
【题型2 已知三角形的面积求k】
1．（2023春·浙江台州·九年级统考期末）如图，放置含30°的直角三角板，使点B在y轴上，点C在双曲线y=kx上，且AB⊥y轴，BC的延长线交x轴于点D，若S△ACD=3．则k=（ ）
A．3B．33C．6D．9
2．（2023春·重庆巴南·九年级统考期末）如图，在平面直角坐标系中，反比例函数y=kx（k<0，x<0）的图象经过AB上的两点A，P，其中P为AB的中点，若△AOB的面积为18．则k的值为（ ）
A．−18B．−12C．−9D．−6
3．（2023春·江西宜春·九年级校考期末）如图，在平面直角坐标系中，Rt△ABC的斜边AB的中点与坐标原点重合，点D是x轴上一点，连接CD、AD．若CB平分∠OCD，反比例函数y=kx(k<0,x<0)的图象经过CD上的两点C、E，且CE=DE，△ACD的面积为12，则k的值为（ ）
A．－4B．－8C．－12D．－16
第II卷（非选择题）
请点击修改第II卷的文字说明
二、填空题
4．（2023春·浙江宁波·九年级校考期中）如图，在平面直角坐标系中，等边三角形ABC的一条边AB⊥x轴于点B，经过点A的反比例函数y=kx（k>0，x>0）的图象交BC于点D，连结OA，OC，若点D是BC中点，△OAC的面积为3，则k的值为 ．

5．（2023春·山东烟台·九年级统考期末）如图，平行四边形ABCD的顶点A在x轴上，点D在y=kxk>0上，且AD⊥x轴，CA的延长线交y轴于点E．若S△ABE=72，则k= ．

6．（2023春·四川成都·九年级校考期中）如图，直线y＝13x与双曲线y＝kx平交于A、B两点，直线BC经过点B，与双曲线y＝kx交于另一点C，∠ABC＝45°，连接AC，若△ABC的面积是35，则k＝ ．
7．（2023春·黑龙江大庆·九年级统考期末）如图，在平面角坐标系中，矩形ABCD的对角线AC的中点与坐标原点重合，点E是x轴上一点，连接AE．若AD平分∠OAE，反比例函数y=kx(k>0,x>0)的图象经过AE上的两点A，F，且AF=EF,△ABE的面积为18，则k的值为 ．
【题型3 根据k的几何意义求四边形的面积】
1．（2023春·四川巴中·九年级统考期末）如图，点A是反比例函数y=−8xx<0的图像上的一点，过点A作平行四边形ABCD．使点B,C在x轴上，点D在y轴上，则平行四边形ABCD的面积为（ ）
A．2B．4C．8D．16
2．（2023春·江苏·九年级统考期末）如图，四边形AOBC和四边形CDEF都是正方形，边OA在x轴上，边OB在y轴上，点D在边CB上，反比例函数y= −8x 在第二象限的图象经过点E，则正方形AOBC和正方形CDEF的面积之差为（ ）
A．12 B．10 C．8 D．6
3．（2023春·全国·九年级期中）如图，平行四边形OABC的顶点O，B在y轴上，顶点A在y＝k1x（k1＜0）上，顶点C在y＝k2x（k2＞0）上，则平行四边形OABC的面积是 ．
4．（2023春·山东烟台·九年级统考期中）如图，反比例函数y=2x(x>0)的图象经过矩形OABC对角线OB的中点P，与AB、BC交于E、F两点，则四边形OEBF的面积是 ．

5．（2023春·山西大同·九年级大同一中校考期末）如图所示，矩形OABC的边OA在x轴上，OC在y轴上，反比例函数y=kx的图象x经过BC边上的点D和AB边上的点E，若D好是BC的中点，其坐标为(2,3)，连接OD、OE，则四边形ODBE的面积为 ．

6．（2023春·河南南阳·九年级统考期末）如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A，B两点的纵坐标分别为3，1，反比例函数y＝3x的图象经过A，B两点，则菱形ABCD的面积为 ．
7．（2023春·江苏常州·九年级统考期末）在平面直角坐标系中，反比例函数y=kxx>0的图像与一次函数y=mx+bm<0的图像在第一象限交于A、B两点．
探究一：
P是平面内的一点，过点A、B、P分别作x轴、y轴的垂线，相应的两条垂线与坐标轴所围成的矩形面积记为SA、SB、SP，矩形周长记为CA、CB、CP，
（1）如图1，P是线段AB上不与点A、B重合的一点，k=8．
SA=______，SA______SP（填“＞”、“＜”或“＝”）：
猜想：当点P从点A运动到点B时，SP的变化规律是____________；
（2）如图2，P是双曲线AB段上不与点A、B重合的一点，m=−1，b=4．
CA=______，CA______CP（填“＞”、“＜”或“＝”）；
猜想：当点P从点A运动到点B时，CP的变化规律是____________；
探究二：
如图3，过点A作x轴的垂线，过点B作y轴的垂线，两条垂线交于直线AB右上方的点Q，OQ与反比例函数的图像交于点G．若G是OQ的中点，且△QAB的面积为9，求k的值．

【题型4 已知四边形的面积求k】
1．（2023春·广东茂名·九年级茂名市第一中学校考期中）如图，在平面直角坐标系中，四边形OABC是矩形，四边形ADEF是正方形，点A，D在x轴的正半轴上，点C在y轴的正半轴上，点F在AB上，点B，E在反比例函数y＝kx（x＞0，k＞0）的图象上，若正方形ADEF的面积为4，且BF＝AF，则k的值（ ）
A．3B．6C．8D．12
2．（2023春·山东济南·九年级统考期末）如图，正方形ABCD的相邻两个顶点C、D分别在x轴、y轴上，且满足BD∥x轴，反比例函数y＝kx（x＜0）的图象经过正方形的中心E，若正方形的面积为8，则该反比例函数的解析式为（ ）
A．y＝4xB．y＝－4xC．y＝8xD．y＝－8x
3．（2023春·江苏苏州·九年级统考期中）如图，四边形OABC是矩形，点A在x轴正半轴，点C在y轴正半轴，对角线OB，CA交于点D．双曲线y=kx(k≠0)经过点D与边BC，AB分别交于点E，点F，连接DE，DF，若四边形BEDF的面积为5，则k的值为（ ）
A．5B．52C．53D．103
4．（2023春·山东德州·九年级统考期末）如图，矩形OABC与反比例函数y1=k1x（k1是非零常数，x>0）的图象交于点M，N，与反比例函数y2=k2x（k2是非零常数，x>0）的图象交于点B，连接OM，ON． 若四边形OMBN的面积为3，则k2−k1=( )
A．3B．-3C．32D．6
5．（2023春·重庆万州·九年级重庆市万州高级中学统考期中）如图，平行四边形ABOC中，对角线交于点E，双曲线y＝kx(k<0)经过C、E两点，若平行四边形ABOC的面积为18，则k的值是（ ）
A．﹣3B．﹣4C．﹣5D．﹣6
6．（2023春·江苏无锡·九年级校考期中）如图，在平面直角坐标系中，菱形ABCD的顶点A，B在反比例函数y=kx（k>0，x>0）的图象上，横坐标分别为1，4，对角线BD∥x轴．若菱形ABCD的面积为452，则k的值为（ ）
A．54B．154C．4D．5
7．（2023春·河南平顶山·九年级统考期末）如图，四边形OABC是平行四边形，其面积为8，点A在反比例函数y=3x的图象上，过点A作AD//x轴交BC于点D，过点D的反比例函数图象关系式为y=kx，则k的值是 ．
【题型5 根据k的几何意义求坐标】
1．（2023春·山东烟台·九年级统考期末）如图，平行四边形OABC的顶点A在x轴的正半轴上，点D2,1在对角线OB上，反比例函数y=kxk>0,x>0的图象经过C、D两点．已知平行四边形OABC的面积是6，则点B的坐标为（ ）
A．4,83B．4,2C．5,2.5D．245,125
2．（2023春·江西上饶·九年级统考期末）如图，已知矩形OABC的顶点B（-8，6）在反比例函数y=kx的图象上，点A在x轴上，点C在y轴上，点P在反比例函数y=kx的图象上，且横坐标为a（a<-8），分别过点P作PE⊥x轴于点E， PF⊥y轴于点F，交AB于点G．
(1)求反比例函数的解析式；
(2)若四边形PEAG为正方形，求点P的坐标；
(3)连接OP交AB于点M，BM：MA=3：2，求四边形PEAM与四边形BMOC的面积比．
3．（2023春·河南南阳·九年级统考期中）如图，长方形OABC的两边OA、OC分别在两坐标轴上，反比例函数y=kxx>0)的图象分别与AB、BC相交于点D、E，EM⊥x轴交x轴于点M，交OD于点F．已知：S四边形COME=6,OA=5,OC=2．

(1)求反比例函数的解析式；
(2)求点D、F的坐标；
(3)求△OED的面积．
4．（2023春·浙江温州·九年级统考期末）如图，点Am，1和点B在反比例函数y=kxk>0，x>0的图象上，过点A作AC∥y轴交x轴于点C，过点B作BD∥x轴交直线AC于点D，CD=3AC．

(1)若AD=BD，求k的值．
(2)连结OB，若四边形OBDC的面积为6，求点B的坐标．
5．（2023春·四川成都·九年级统考期末）如图，已知A(2,4)是正比例函数函数y=kx的图象与反比例函数y=mx的图象的交点．
(1)求反比例函数和正比例函数的解析式；
(2)B为双曲线上点A右侧一点，连接OB,AB．若△OAB的面积为15，求点B的坐标．
6．（2023春·江苏·九年级期末）如图，一次函数y=12x−2的图象分别交x轴、y轴于A、B，P为AB上一点且PC为△AOB的中位线，PC的延长线交反比例函数y=kxk>0的图象于Q，S△OQC=32，则k的值和Q点的坐标分别为 ．
7．（2023春·安徽滁州·九年级校考期中）如图，平行于y轴的直尺（部分）与反比例函数y=mx(x>0)的图像交于A，C两点与x轴交于B，D两点，连接AC，点A，B对应直尺上的刻度分别为5，2，直尺的宽度BD=2，S△AOC=5，则点C的坐标是 ．
【题型6 根据k的几何意义判断面积的变化情况】
1．（2023春·浙江绍兴·九年级统考期末）如图，等腰三角形△ABC的顶点A在原点固定，且始终有AC=BC，当顶点C在函数y=kxx>0的图象上从上到下运动时，顶点B在x轴的正半轴上移动，则△ABC的面积大小变化情况是（ ）
A．先减小后增大B．先增大后减小C．一直不变D．先增大后不变
2．（2023·江苏连云港·校联考三模）如图，在平面直角坐标系中，点Ba,b是反比例函数y≤4x在第三象限图像上的一个动点，以B为顶点，原点对称中心作矩形ABCD，AB⊥x轴于点E，过点O的直线MQ分别交AD、BC边于点M、Q，以MQ为一边作矩形MNPQ，且直线PN恰好经过点E，如果点B在运动中横坐标逐渐变小，那么矩形MNPQ的面积的大小变化情况是（ ）

A．先减小后增大B．先增大后减小C．一直不变D．一直减小
3．（2023春·湖南常德·九年级统考期中）如图，点M是反比例函数y=5x(x>0)图像上的一个动点，过点M作x轴的平行线交反比例函数y=−5xx<0图像于点N．
(1)若点M（53，3），求点N的坐标；
(2)若点P是x轴上的任意一点，那么△PMN的面积是否发生变化？若不变，求出它的面积是多少？若变化，请说明理由．
4．（2023春·全国·九年级专题练习）如图，一次函数y＝x+1的图象与反比例函数的图象交于点A（1，n）．
（1）求反比例函数的表达式；
（2）点P（m，0）在x轴上一点，点M是反比例函数图象上任意一点，过点M作MN⊥y轴，求出△MNP的面积；
（3）在（2）的条件下，当点P从左往右运动时，判断△MNP的面积如何变化？并说明理由．
5．（2023·九年级课时练习）如图，P1是反比例函数y=kx(k>0)在第一象限图象上一点，点A1的坐标为(1, 0)．
(1)当点P1的横坐标逐渐增大时，△P1OA1的面积将如何变化？
(2)若△P1OA1与△P2A1A2均为直角三角形，其中∠P1OA1=P2A1A2=60∘，求此反比例函数的解析式及点A2的坐标．