







高教版(2021)拓展模块二 下册6.1.2 两角和与差的正弦公式完美版ppt课件
展开6.1.2 两角和与差的正弦公式
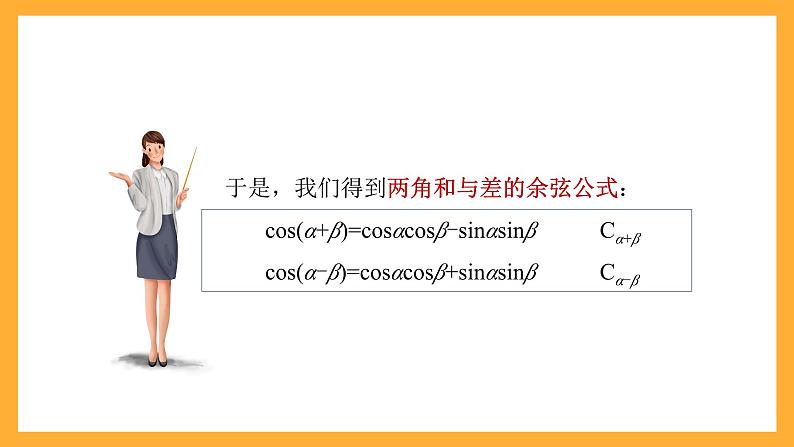
上一节学习了α±β的余弦,即cs(α±β)可以用α、β的正弦、余弦来表示.那么,α±β的正弦,即sin(α±β)是否也可以用α、β的正弦、余弦来表示呢?
在上式中,用-β代替β,可得├ sin[?+(−?)]=sin?cs(−?)+cs?sin(−?)即sin(?−?)=sin?cs?−cs?sin?.
(1) 读书部分: 教材章节6.1.2; (2) 书面作业: P10习题6.1的1(1)(4),2(1).
中职数学高教版(2021)拓展模块二 下册7.2.2 等差数列前n项和公式精品课件ppt: 这是一份中职数学高教版(2021)拓展模块二 下册<a href="/sx/tb_c4035833_t3/?tag_id=26" target="_blank">7.2.2 等差数列前n项和公式精品课件ppt</a>,文件包含中职数学高教版2021·拓展模块一下册722等差数列前n项和公式课件pptx、中职数学高教版2021·拓展模块一下册722等差数列前n项和公式教案doc、天坛圜丘坛高考题mp4等3份课件配套教学资源,其中PPT共16页, 欢迎下载使用。
中职数学高教版(2021)拓展模块二 下册6.4.1 三角形面积公式完整版课件ppt: 这是一份中职数学高教版(2021)拓展模块二 下册<a href="/sx/tb_c4035825_t3/?tag_id=26" target="_blank">6.4.1 三角形面积公式完整版课件ppt</a>,文件包含中职数学高教版2021·拓展模块一下册641三角形面积公式课件pptx、中职数学高教版2021·拓展模块一下册641三角形面积公式教案doc、三角形面积公式的推导mp4等3份课件配套教学资源,其中PPT共13页, 欢迎下载使用。
中职数学高教版(2021)拓展模块二 下册6.2 二倍角公式完美版课件ppt: 这是一份中职数学高教版(2021)拓展模块二 下册<a href="/sx/tb_c4035822_t3/?tag_id=26" target="_blank">6.2 二倍角公式完美版课件ppt</a>,文件包含中职数学高教版2021·拓展模块一下册62二倍角公式课件pptx、中职数学高教版2021·拓展模块一下册62二倍角公式教案doc等2份课件配套教学资源,其中PPT共15页, 欢迎下载使用。












