新高考数学二轮培优大题优练3 统计（2份打包，原卷版+教师版）

这是一份新高考数学二轮培优大题优练3 统计（2份打包，原卷版+教师版），文件包含新高考数学二轮培优大题优练3统计原卷版doc、新高考数学二轮培优大题优练3统计教师版doc等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。

优选例题
例1．某家水果店的店长为了解本店苹果的日销售情况，记录了近期连续120天苹果的日销售量(单位： SKIPIF 1 < 0 )，并绘制频率分布直方图如下：
（1）请根据频率分布直方图估计该水果店苹果日销售量的众数和平均数；(同一组中的数据以这组数据所在区间中点的值作代表)
（2）一次进货太多，水果会变得不新鲜；进货太少，又不能满足顾客的需求．店长希望每天的苹果尽量新鲜，又能80%地满足顾客的需求(在10天中，大约有8天可以满足顾客的需求)．请问每天应该进多少千克苹果？(精确到整数位)
【答案】（1）众数为85，平均数为 SKIPIF 1 < 0 ；（2）每天应该进98千克苹果．
【解析】（1）如图示：区间 SKIPIF 1 < 0 频率最大，所以众数为85，
平均数为： SKIPIF 1 < 0
SKIPIF 1 < 0 ．
（2）日销售量 SKIPIF 1 < 0 的频率为 SKIPIF 1 < 0 ，日销量 SKIPIF 1 < 0 的频率为 SKIPIF 1 < 0 ，
故所求的量位于 SKIPIF 1 < 0 ，
由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，
故每天应该进98千克苹果．
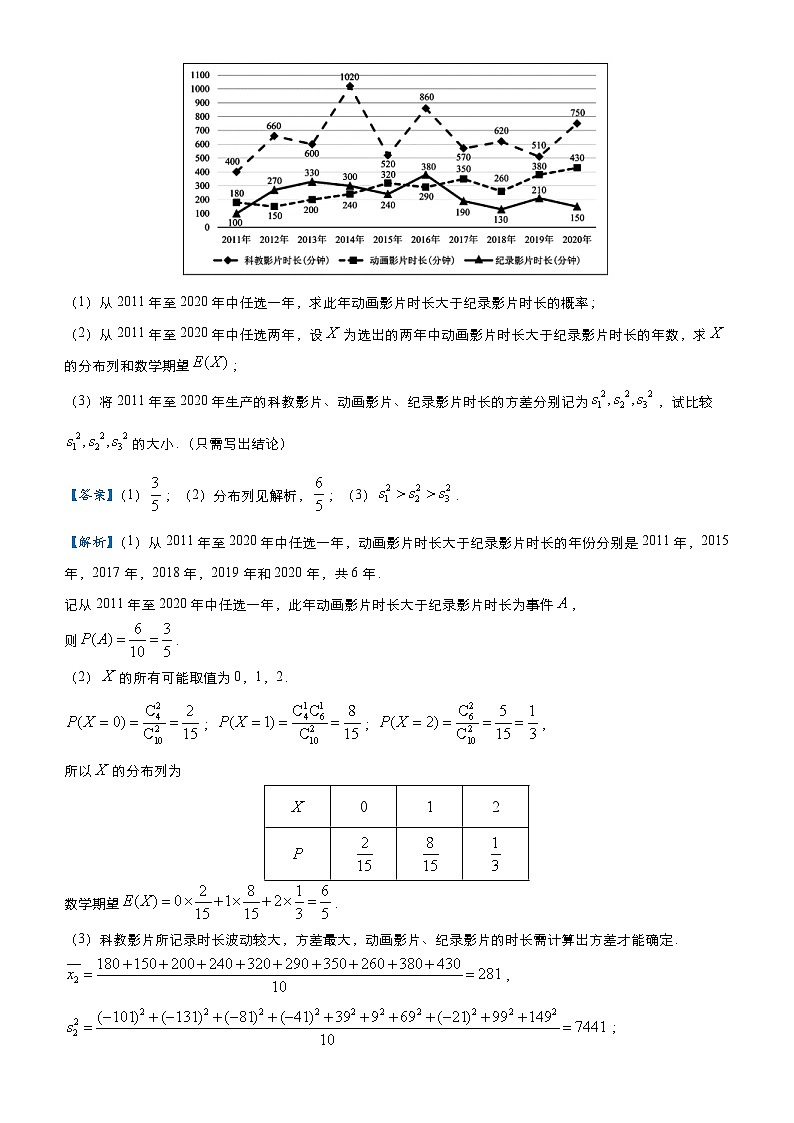
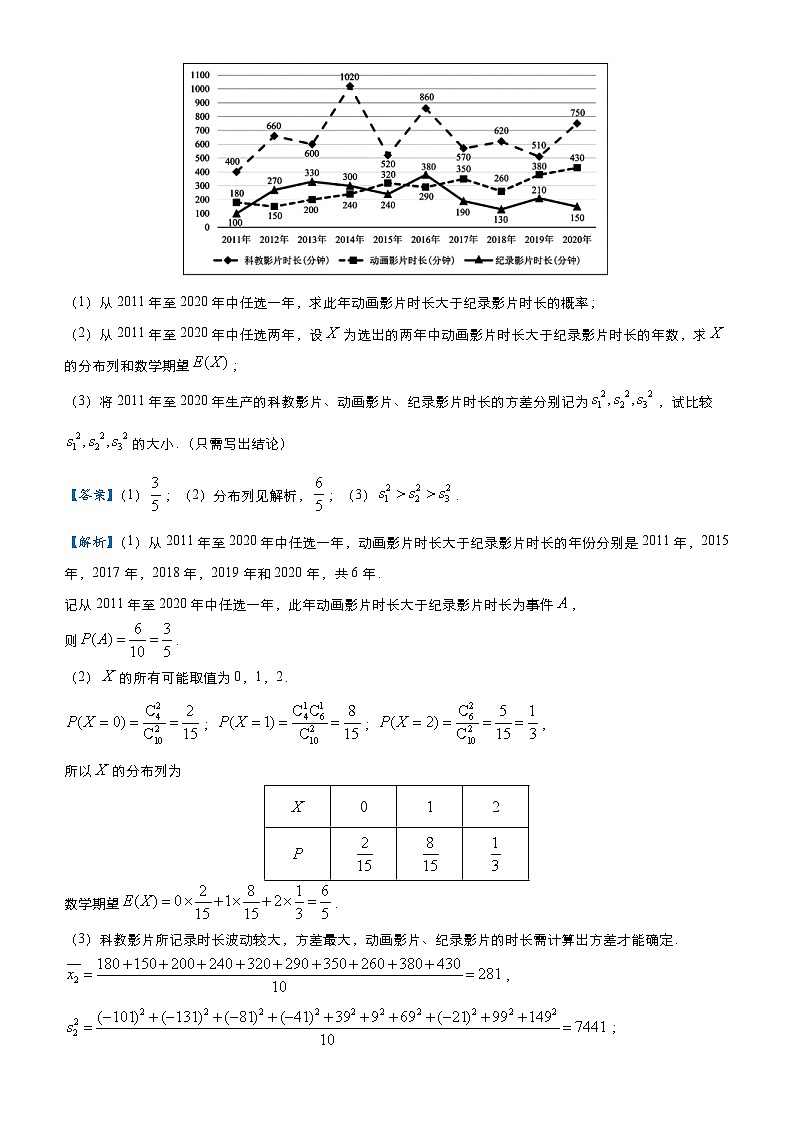
例2．某电影制片厂从2011年至2020年生产的科教影片、动画影片、纪录影片的时长（单位：分钟）如图所示．
（1）从2011年至2020年中任选一年，求此年动画影片时长大于纪录影片时长的概率；
（2）从2011年至2020年中任选两年，设 SKIPIF 1 < 0 为选出的两年中动画影片时长大于纪录影片时长的年数，求 SKIPIF 1 < 0 的分布列和数学期望 SKIPIF 1 < 0 ；
（3）将2011年至2020年生产的科教影片、动画影片、纪录影片时长的方差分别记为 SKIPIF 1 < 0 ，试比较 SKIPIF 1 < 0 的大小．（只需写出结论）
【答案】（1） SKIPIF 1 < 0 ；（2）分布列见解析， SKIPIF 1 < 0 ；（3） SKIPIF 1 < 0 ．
【解析】（1）从2011年至2020年中任选一年，动画影片时长大于纪录影片时长的年份分别是2011年，2015年，2017年，2018年，2019年和2020年，共6年．
记从2011年至2020年中任选一年，此年动画影片时长大于纪录影片时长为事件 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ．
（2） SKIPIF 1 < 0 的所有可能取值为0，1，2．
SKIPIF 1 < 0 ； SKIPIF 1 < 0 ； SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 的分布列为
数学期望 SKIPIF 1 < 0 ．
（3）科教影片所记录时长波动较大，方差最大，动画影片、纪录影片的时长需计算出方差才能确定．
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ；
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ．
例3．2017高考特别强调了要增加对数学文化的考查，为此某校高三年级特命制了一套与数学文化有关的专题训练卷（文、理科试卷满分均为 SKIPIF 1 < 0 分），并对整个高三年级的学生进行了测试．现从这些学生中随机抽取了 SKIPIF 1 < 0 名学生的成绩，按照成绩为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 分成了 SKIPIF 1 < 0 组，制成了如图所示的频率分布直方图（假定每名学生的成绩均不低于 SKIPIF 1 < 0 分）．
（1）求频率分布直方图中的 SKIPIF 1 < 0 的值，并估计所抽取的 SKIPIF 1 < 0 名学生成绩的平均数、中位数（同一组中的数据用该组区间的中点值代表）；
（2）若高三年级共有 SKIPIF 1 < 0 名学生，试估计高三学生中这次测试成绩不低于 SKIPIF 1 < 0 分的人数；
（3）若利用分层抽样的方法从样本中成绩不低于 SKIPIF 1 < 0 分的三组学生中抽取 SKIPIF 1 < 0 人，再从这 SKIPIF 1 < 0 人中随机抽取 SKIPIF 1 < 0 人参加这次考试的考后分析会，试求后两组中至少有 SKIPIF 1 < 0 人被抽到的概率．
【答案】（1）74， SKIPIF 1 < 0 ；（2）1200；（3） SKIPIF 1 < 0 ．
【解析】（1）由频率分布直方图可得第4组的频率为 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ．
故可估计所抽取的50名学生成绩的平均数为
SKIPIF 1 < 0 （分）．
由于前两组的频率之和为 SKIPIF 1 < 0 ，前三组的频率之和为 SKIPIF 1 < 0 ，
故中位数在第3组中．
设中位数为 SKIPIF 1 < 0 分，则有 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
即所求的中位数为 SKIPIF 1 < 0 分．
（2）由（1）可知，50名学生中成绩不低于70分的频率为 SKIPIF 1 < 0 ，
由以上样本的频率，可以估计高三年级2000名学生中成绩不低于70分的人数为 SKIPIF 1 < 0 ．
（3）由（1）可知，后三组中的人数分别为15，10，5，
故这三组中所抽取的人数分别为3，2，1．
记成绩在 SKIPIF 1 < 0 这组的3名学生分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，成绩在 SKIPIF 1 < 0 这组的2名学生分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
成绩在 SKIPIF 1 < 0 这组的1名学生为 SKIPIF 1 < 0 ，
则从中任抽取3人的所有可能结果为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 共20种，
其中后两组中没有人被抽到的可能结果为 SKIPIF 1 < 0 ，只有1种，
故后两组中至少有1人被抽到的概率为 SKIPIF 1 < 0 ．
模拟优练
1． SKIPIF 1 < 0 年 SKIPIF 1 < 0 月，习近平总书记对制止餐饮浪费行为作出重要指示，要求进一步加强宣传教育，切实培养节约习惯，在全社会营造浪费可耻、节约光荣的氛围．为贯彻总书记指示，大庆市某学校食堂从学生中招募志愿者，协助食堂宣传节约粮食的相关活动．现已有高一 SKIPIF 1 < 0 人，高二 SKIPIF 1 < 0 人，高三 SKIPIF 1 < 0 人报名参加志愿活动．根据活动安排，拟采用分层抽样的方法，从已报名的志愿者中抽取 SKIPIF 1 < 0 名志愿者，参加为期 SKIPIF 1 < 0 天的第一期志愿活动．
（1）第一期志愿活动需从高一、高二、高三报名的学生中各抽取多少人？
（2）现在要从第一期志愿者中的高二、高三学生中抽取 SKIPIF 1 < 0 人去粘贴宣传标语，设这 SKIPIF 1 < 0 人中含有高二学生 SKIPIF 1 < 0 人，求随机变量 SKIPIF 1 < 0 的分布列；
（3）食堂每天约有 SKIPIF 1 < 0 人就餐，其中一组志愿者的任务是记录学生每天倒掉的剩菜剩饭的重量（单位：公斤），以 SKIPIF 1 < 0 天为单位来衡量宣传节约粮食的效果．在一个周期内，这组志愿者记录的数据如下：
前 SKIPIF 1 < 0 天剩菜剩饭的重量为： SKIPIF 1 < 0 ；
后 SKIPIF 1 < 0 天剩菜剩饭的重量为： SKIPIF 1 < 0 ，
借助统计中的图、表、数字特征等知识，分析宣传节约粮食活动的效果（选择一种方法进行说明即可）．
【答案】（1）6人，4人，2人；（2）答案见解析；（3）答案见解析．
【解析】（1）报名的学生共有126人，抽取的比例为 SKIPIF 1 < 0 ，
所以高一抽取 SKIPIF 1 < 0 人，高二抽取 SKIPIF 1 < 0 人，高三抽取 SKIPIF 1 < 0 人．
（2）随机变量X的取值为2，3，4，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
所以随机变量X的分布列为
（3）法一、（数字特征）前10天的平均值为 SKIPIF 1 < 0 ，后10天的平均值为 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，
所以宣传节约粮食活动的效果很好．
法二：（茎叶图）画出茎叶图
因为前10天的重量集中在23，24附近，而后10天的重量集中在20附近，
所以节约宣传后剩饭剩菜明显减少，宣传效果很好．
2．为了推进分级诊疗，实现“基层首诊､双向转诊､急慢分治､上下联动”的诊疗模式，某城市自2020年起全面推行家庭医生签约服务．已知该城市居民约为1000万，从0岁到100岁的居民年龄结构的频率分布直方图如图1所示．为了解各年龄段居民签约家庭医生的情况，现调查了1000名年满18周岁的居民，各年龄段被访者签约率如图2所示．
（1）估计该城市年龄在50岁以上且已签约家庭医生的居民人数；
（2）据统计，该城市被访者的签约率约为44%，为把该城市年满18周岁居民的签约率提高到55%以上，
应着重提高图2中哪个年龄段的签约率？并根据已有数据陈述理由．
【答案】（1） SKIPIF 1 < 0 万；（2）应着重提高30-50这个年龄段的签约率，理由见解析．
【解析】（1）该城市年龄在50-60岁的签约人数为 SKIPIF 1 < 0 万；
在60-70岁的签约人数为 SKIPIF 1 < 0 万；
在70-80岁的签约人数为 SKIPIF 1 < 0 万；
在80岁以上的签约人数为 SKIPIF 1 < 0 万；
故该城市年龄在50岁以上且已签约家庭医生的居民人数为： SKIPIF 1 < 0 万．
（2）年龄在10-20岁的人数为： SKIPIF 1 < 0 万；
年龄在20-30岁的人数为： SKIPIF 1 < 0 万．
所以，年龄在18-30岁的人数大于180万，小于230万，签约率为 SKIPIF 1 < 0 ；
年龄在30-50岁的人数为 SKIPIF 1 < 0 万，签约率为 SKIPIF 1 < 0 ．
年龄在50岁以上的人数为 SKIPIF 1 < 0 万，签约率超过55%，上升空间不大．
故由以上数据可知这个城市在30-50岁这个年龄段的人数为370万，基数较其他年龄段是最大的，且签约率非常低，所以为把该地区满18周岁居民的签约率提高到以上，应着重提高30-50这个年龄段的签约率．
3．习近平总书记在党的十九大工作报告中提出，永远把人民对美好生活的向往作为奋斗目标．在这一号召的引领下，全国人民积极工作，健康生活．当前，“日行万步”正成为健康生活的代名词．某学校工会积极组织该校教职工参与“日行万步”活动．界定日行步数不足 SKIPIF 1 < 0 千步的人为“不健康生活方式者”，不少于 SKIPIF 1 < 0 千步的人为“超健康生活方式者”，其他为“一般生活方式者”．某日，学校工会随机抽取了该校 SKIPIF 1 < 0 名教职工，统计他们的日行步数，按步数分组，得到频率分布直方图如图所示：
（1）求 SKIPIF 1 < 0 名教职工日行步数（千步）的样本平均数（结果四舍五入保留整数）；
（2）由直方图可以认为该校教职工的日行步数 SKIPIF 1 < 0 （千步）服从正态分布 SKIPIF 1 < 0 ，其中 SKIPIF 1 < 0 为样本平均数，标准差 SKIPIF 1 < 0 的近似值为 SKIPIF 1 < 0 ，求该校被抽取的 SKIPIF 1 < 0 名教职工中日行步数（千步） SKIPIF 1 < 0 的人数（结果四舍五入保留整数）；
（3）用样本估计总体，将频率视为概率．若工会从该校教职工中随机抽取 SKIPIF 1 < 0 人作为“日行万步”活动的慰问奖励对象，规定：“不健康生活方式者”给予精神鼓励，奖励金额每人 SKIPIF 1 < 0 元；“一般生活方式者”奖励金额每人 SKIPIF 1 < 0 元；“超健康生活方式者”奖励金额每人 SKIPIF 1 < 0 元．求工会慰问奖励金额 SKIPIF 1 < 0 的分布列和数学期望．
附：若随机变量 SKIPIF 1 < 0 服从正态分布 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
【答案】（1）见解析；（2）54人；（3）分布列见解析，200．
【解析】（1） SKIPIF 1 < 0 SKIPIF 1 < 0 ．
（2）∵ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
走路步数 SKIPIF 1 < 0 的总人数为 SKIPIF 1 < 0 人．
（3）由题意知 SKIPIF 1 < 0 的可能取值为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
则 SKIPIF 1 < 0 的分布列为：
SKIPIF 1 < 0 ．
4．随着经济模式的改变，微商和电商已成为当今城乡一种新型的购销平台．已知经销某种商品的电商在任何一个销售季度内，每售出 SKIPIF 1 < 0 吨该商品可获利润 SKIPIF 1 < 0 万元，未售出的商品，每 SKIPIF 1 < 0 吨亏损 SKIPIF 1 < 0 万元．根据往年的销售经验，得到一个销售季度内市场需求量的频率分布直方图如图所示．已知电商为下一个销售季度筹备了 SKIPIF 1 < 0 吨该商品．现以 SKIPIF 1 < 0 （单位：吨， SKIPIF 1 < 0 ）表示下一个销售季度的市场需求量， SKIPIF 1 < 0 （单位：万元）表示该电商下一个销售季度内经销该商品获得的利润．
（1）将 SKIPIF 1 < 0 表示为 SKIPIF 1 < 0 的函数，求出该函数表达式；
（2）根据直方图估计利润 SKIPIF 1 < 0 不少于57万元的概率；
（3）根据频率分布直方图，估计一个销售季度内市场需求量 SKIPIF 1 < 0 的平均数与中位数的大小（保留到小数点后一位）．
【答案】（1） SKIPIF 1 < 0 ；（2） SKIPIF 1 < 0 ；（3）平均数为 SKIPIF 1 < 0 （吨），估计中位数应为 SKIPIF 1 < 0 （吨）．
【解析】（1）当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
所以， SKIPIF 1 < 0 ．
（2）根据频率分布直方图及（1）知，
当 SKIPIF 1 < 0 时，由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时，由 SKIPIF 1 < 0 ，
所以，利润 SKIPIF 1 < 0 不少于57万元当且仅当 SKIPIF 1 < 0 ，
于是由频率分布直方图可知市场需求量 SKIPIF 1 < 0 的频率为
SKIPIF 1 < 0 ，
所以下一个销售季度内的利润 SKIPIF 1 < 0 不少于57万元的概率的估计值为 SKIPIF 1 < 0 ．
（3）估计一个销售季度内市场需求量 SKIPIF 1 < 0 的平均数为
SKIPIF 1 < 0 SKIPIF 1 < 0 （吨），
由频率分布直方图易知，
由于 SKIPIF 1 < 0 时，对应的频率为 SKIPIF 1 < 0 ，
而 SKIPIF 1 < 0 时，对应的频率为 SKIPIF 1 < 0 ，
因此一个销售季度内市场需求量 SKIPIF 1 < 0 的中位数应属于区间 SKIPIF 1 < 0 ，于是估计中位数应为 SKIPIF 1 < 0 （吨）．
5．某微商对某种产品每天的销售量x件进行为期一个月的数据统计分析，并得出了该月销售量的直方图
（一个月按30天计算）如图所示．假设用直方图中所得的频率来估计相应的事件发生的概率．
（1）求频率分布直方图中的 SKIPIF 1 < 0 的值；
（2）求日销量的平均值（同一组中的数据用该组区间的中点值作代表）；
（3）若微商在一天的销售量不低于25件，则上级商企会给微商赠送100元的礼金，估计该微商在一年内获得的礼金数．
【答案】（1） SKIPIF 1 < 0 ；（2） SKIPIF 1 < 0 ；（3） SKIPIF 1 < 0 （元）．
【解析】（1）由题意可得 SKIPIF 1 < 0 ．
（2）根据已知的频率分布直方图，日销售量的平均值为：
SKIPIF 1 < 0 ．
（3）根据频率分布直方图，日销售量不低于25件的天数为： SKIPIF 1 < 0 ，
可获得的奖励为900元，
依此可以估计一年内获得的礼金数为 SKIPIF 1 < 0 元．
6．某公司计划购买1台机器，该种机器使用三年后即被淘汰．机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元．在机器使用期间，如果备件不足再购买，则每个500元．现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：
记x表示1台机器在三年使用期内需更换的易损零件数，y表示1台机器在购买易损零件上所需的费用（单位：元）， SKIPIF 1 < 0 表示购机的同时购买的易损零件数．
（1）若 SKIPIF 1 < 0 ，求y与x的函数解析式；
（2）若要求“需更换的易损零件数不大于 SKIPIF 1 < 0 ”的频率不小于 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的最小值；
（3）假设这100台机器在购机的同时每台都购买19个易损零件，或每台都购买20个易损零件，分别计算这100台机器在购买易损零件上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买19个还是20个易损零件？
【答案】（1） SKIPIF 1 < 0 ；（2）19；（3）购买1台机器的同时应购买19个易损零件．
【解析】（1）当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
所以与的函数解析式为 SKIPIF 1 < 0 ．
（2）由柱状图知，需更换的零件数不大于18的频率为 SKIPIF 1 < 0 ，不大于19的频率为 SKIPIF 1 < 0 ，
故的最小值为19．
（3）若每台机器在购机同时都购买19个易损零件，
则这100台机器中有70台在购买易损零件上的费用为3800，20台的费用为4300，10台的费用为4800，
因此这100台机器在购买易损零件上所需费用的平均数为 SKIPIF 1 < 0 ；
若每台机器在购机同时都购买20个易损零件，
则这100台机器中有90台在购买易损零件上的费用为4000，10台的费用为4500，
因此这100台机器在购买易损零件上所需费用的平均数为 SKIPIF 1 < 0 ，
比较两个平均数可知，购买1台机器的同时应购买19个易损零件．
7．某花卉企业引进了数百种不同品种的康乃馨，通过试验田培育，得到了这些康乃馨种子在当地环境下的发芽率，并按发芽率分为 SKIPIF 1 < 0 组： SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 加以统计，得到如图所示的频率分布直方图．企业对康乃馨的种子进行分级，将发芽率不低于 SKIPIF 1 < 0 的种子定为“ SKIPIF 1 < 0 级”，发芽率低于 SKIPIF 1 < 0 但不低于 SKIPIF 1 < 0 的种子定为“ SKIPIF 1 < 0 级”，发芽率低于 SKIPIF 1 < 0 的种子定为“ SKIPIF 1 < 0 级”．
（1）现从这些康乃馨种子中随机抽取一种，估计该种子不是“ SKIPIF 1 < 0 级”种子的概率；
（2）该花卉企业销售花种，且每份“ SKIPIF 1 < 0 级”、“ SKIPIF 1 < 0 级”、“ SKIPIF 1 < 0 级”康乃馨种子的售价分别为 SKIPIF 1 < 0 元、 SKIPIF 1 < 0 元、 SKIPIF 1 < 0 元．某人在市场上随机购买了该企业销售的康乃馨种子两份，共花费 SKIPIF 1 < 0 元，以频率为概率，求 SKIPIF 1 < 0 的分布列和数学期望；
（3）企业改进了花卉培育技术，使得每种康乃馨种子的发芽率提高到原来的 SKIPIF 1 < 0 倍，那么对于这些康乃馨的种子，与旧的发芽率数据的方差相比，技术改进后发芽率数据的方差是否发生变化？若发生变化，是变大了还是变小了？（结论不需要证明）．
【答案】（1） SKIPIF 1 < 0 ；（2）分布列见解析，数学期望为 SKIPIF 1 < 0 ；（3）方差变大了．
【解析】（1）设事件 SKIPIF 1 < 0 为：“从这些康乃馨种子中随机抽取一种，且该种子不是“ SKIPIF 1 < 0 级”种子”，
由图表，得 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
由图表，知“ SKIPIF 1 < 0 级”种子的频率为 SKIPIF 1 < 0 ，
故可估计从这些康乃馨种子中随机抽取一种，该种子是“ SKIPIF 1 < 0 级”的概率为 SKIPIF 1 < 0 ．
因为事件 SKIPIF 1 < 0 与事件“从这些康乃馨种子中随机抽取一种，且该种子是“ SKIPIF 1 < 0 级”种子”为对立事件，
所以事件 SKIPIF 1 < 0 的概率 SKIPIF 1 < 0 ．
（2）由题意，任取一颗种子，恰好是“ SKIPIF 1 < 0 级”康乃馨的概率为 SKIPIF 1 < 0 ，
恰好是“ SKIPIF 1 < 0 级”康乃馨的概率为 SKIPIF 1 < 0 ，
恰好是“ SKIPIF 1 < 0 级”的概率为 SKIPIF 1 < 0 ．
随机变量 SKIPIF 1 < 0 的可能取值有 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，
且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 的分布列为：
故 SKIPIF 1 < 0 的数学期望 SKIPIF 1 < 0 ．
（3）与旧的发芽率数据的方差相比，技术改进后发芽率数据的方差变大了．
SKIPIF 1 < 0
0
1
2
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
2
3
4
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0