新高考数学一轮复习学案第24讲 平行垂直问题（2份打包，原卷版+解析版）

这是一份新高考数学一轮复习学案第24讲 平行垂直问题（2份打包，原卷版+解析版），文件包含新高考数学一轮复习学案第24讲平行垂直问题原卷版doc、新高考数学一轮复习学案第24讲平行垂直问题解析版doc等2份学案配套教学资源，其中学案共81页， 欢迎下载使用。
1.证明空间中直线、平面的平行关系
（1）证明直线与平面平行的常用方法：
①利用定义，证明直线与平面没有公共点，一般结合反证法证明；
②利用线面平行的判定定理，即线线平行线面平行.辅助线的作法为：平面外直线的端点进平面，同向进面，得平行四边形的对边，不同向进面，延长交于一点得平行于第三边的线段；
③利用面面平行的性质定理，把面面平行转化成线面平行；
（2）证明面面平行的常用方法：
①利用面面平行的定义，此法一般与反证法结合；
②利用面面平行的判定定理；
③利用两个平面垂直于同一条直线；
④证明两个平面同时平行于第三个平面.
（3）证明线线平行的常用方法：①利用直线和平面平行的判定定理；②利用平行公理；
2.证明空间中直线、平面的垂直关系
（1）证明线线垂直的方法
①等腰三角形底边上的中线是高；
②勾股定理逆定理；
③菱形对角线互相垂直；
④直径所对的圆周角是直角；
⑤向量的数量积为零；
⑥线面垂直的性质（）；
⑦平行线垂直直线的传递性（∥）.
（2）证明线面垂直的方法
①线面垂直的定义；
②线面垂直的判定（）；
③面面垂直的性质（）；
平行线垂直平面的传递性（∥）；
⑤面面垂直的性质（）.（3）证明面面垂直的方法
①面面垂直的定义；
②面面垂直的判定定理（）.
【典型例题】
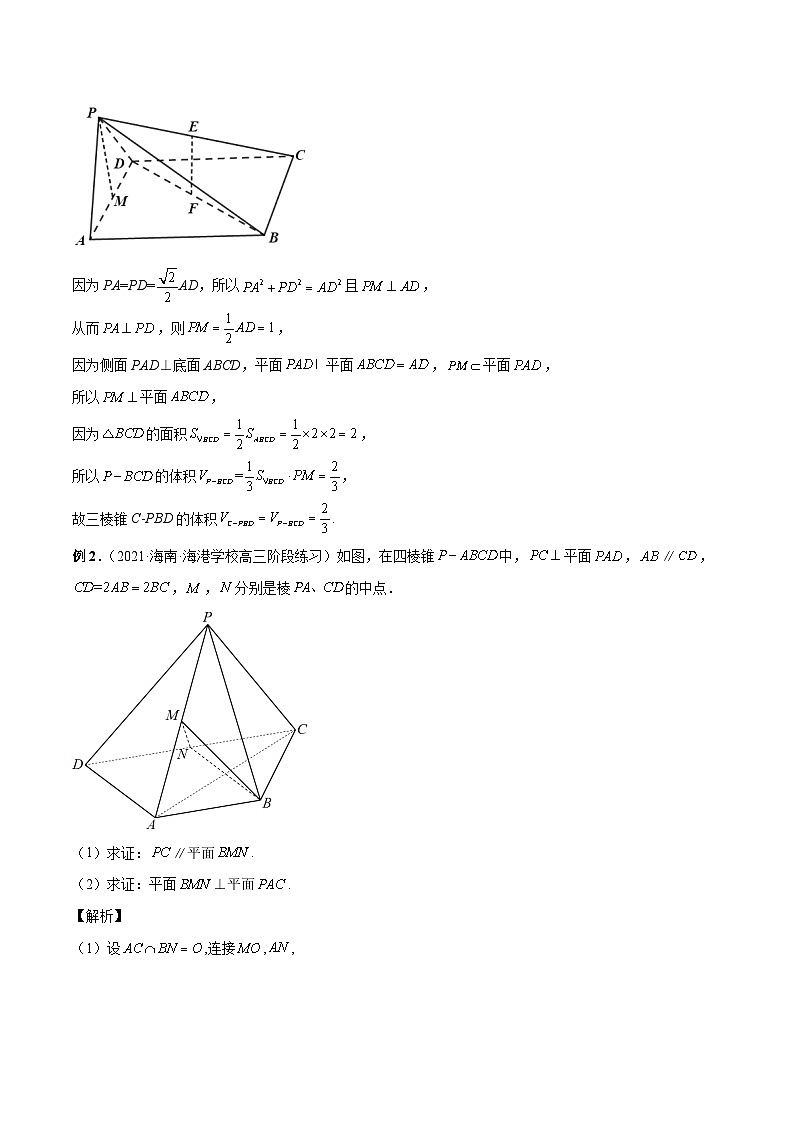
例1．（2021·四川省广安代市中学校高二阶段练习（文））如图，在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，E，F分别为PC，BD的中点，侧面PAD⊥底面ABCD，且PA=PD=AD.
（1）求证：平面PAD；
（2）求三棱锥C-PBD的体积.
【解析】
（1）连接，如下图所示：
因为为中点，且底面ABCD是边长为2的正方形，
所以为中点，
又因为为中点，
所以，
因为平面，平面，
所以平面.
（2）取的中点，连接，如下图所示：
因为PA=PD=AD，所以且，
从而，则，
因为侧面PAD⊥底面ABCD，平面平面，平面，
所以平面，
因为的面积，
所以的体积，
故三棱锥C-PBD的体积.
例2．（2021·海南·海港学校高三阶段练习）如图，在四棱锥中，平面，∥，，，分别是棱的中点．
（1）求证：∥平面.
（2）求证：平面⊥平面.
【解析】
（1）设,连接,,
∥，,是棱的中点, ∥，,
四边形为平行四边形，是棱的中点,∥,
又平面,平面,∥平面.
（2）(方法一)⊥平面,平面,.
∥，,是棱的中点, ∥，,
四边形为平行四边形，∥，.
,四边形为菱形，,
平面,平面,平面,
又平面，平面⊥平面.
（方法二）连接,
平面,平面,
∥,,
平面,平面,,是棱的中点, ,
由（1）可知，,,
又是棱的中点, ,
平面,平面,平面.
又平面,平面⊥平面.
例3．（2021·广西河池·高一阶段练习）如图，四边形ABED为梯形，，，平面ABED，M为AD中点
（1）求证：平面⊥平面PBM
（2）探究在PD上是否存在点G，使得平面PAB，若存在求出G点，若不存在说明理由．
【解析】
（1）证明：连接，因为，，为的中点，所以四边形为菱形，所以，因为平面ABED，平面ABED，所以，因为，面，所以平面，又平面，所以平面平面；
（2）解：当为的中点时，平面，
证明：如图连接，，因为为的中点，为的中点，所以，平面，平面，所以平面，由（1）可知，平面，平面，所以平面，又，平面，所以平面平面，因为平面，所以平面；
例4．（2021·山东潍坊·高二阶段练习）如图，已知在长方体中，，，分别为，，的中点，为线段上非端点的动点，且，，设而与底面的交线为直线，
（1）证明：；
（2）当时，证明：为平面的一条垂线.
【解析】
（1）连结，因为，为，的中点，
所以.
又因为，
所以，
又因为平面，平面,
所以平面，
又因为平面，平面平面，所以.
（2）连接，，
，同理可得，
因为，所以，
同理，
又因为，所以平面，
所以为平面的一条垂线.
【技能提升训练】
1．（2021·江苏·苏州市相城区陆慕高级中学高一阶段练习）如图，P为平行四边形所在平面外一点，，分别是，的中点，平面平面于直线.
（1）判断与平面的位置关系，并证明你的结论；
（2）判断与的位置关系，并证明你的结论.【答案】（1）平面，证明见解析；（2），证明见解析.
【分析】
（1）取PD中点E，连接AE，NE，可得，且，又M为AB中点，可得，且，所以四边形AMNE为平行四边形，可得，根据线面平行的判定定理，可证平面.
（2）根据线面平行的判定定理，可证平面，又平面PBC，结合题意，根据线面平行的性质定理，可证.
【详解】
（1）平面，证明如下：
取PD中点E，连接AE，NE，
因为N，E分别为PC，PD中点，
所以，且，
又M为AB中点，，，
所以，且，
所以四边形AMNE为平行四边形，
所以，
又平面，平面，
所以平面.
（2），证明如下：
因为，平面，平面，
所以平面，
又平面PBC，且平面平面，根据线面平行的性质定理可得.
2．（2021·江苏·南京市中华中学高一期中）如图，在四棱锥中，底面是菱形，分别为，，的中点.
（1）求证：平面；
（2）记平面与底面的交线为，试判断直线与平面的位置关系，并证明.
【答案】（1）证明见解析；（2）直线面，证明见解析.
【分析】
（1）证明，利用线面平行的判定定理即可求证；
（2）由三角形中位线性质可得：，可证明面，由线面平行的性质定理可得，由线面平行的判定定理即可证明直线面.
【详解】
（1）因为分别为，的中点，所以，
因为底面是菱形，所以，所以，
因为平面，平面，
所以平面，
（2）直线与平面平行，证明如下：
因为分别为，的中点，
所以，
因为面，面，所以面，
因为平面与底面的交线为，面，由线面平行的性质定理可得，
因为，所以，
因为面，面，
所以直线面.
3．（2020·江西·赣州市第一中学高二阶段练习（文））如图，PA⊥平面ABCD，四边形ABCD是矩形，PA = AB，点F是PB的中点，点E在边BC上运动.
（1）当点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；
（2）证明：无论点E在边BC的何处，都有PE⊥AF.
【答案】（1）EF//面PAC，理由见解析；（2）证明见解析.
【分析】
（1）当点E为BC的中点时，EF//面PAC，可由线面平行的判定定理给出证明；
（2）转化为证明AF⊥平面PBC即可.
【详解】
（1）当点E为BC的中点时，EF//平面PAC. 理由如下：
∵点E，F分别是BC，PB的中点，∴EF//PC，
又平面，平面，∴EF//平面PAC.
（2）证明：∵PA⊥平面ABCD，平面，∴BC⊥PA，
又四边形ABCD是矩形，∴BC⊥AB，又PA∩AB=A，∴BC⊥平面PAB，
又平面，∴ AF⊥BC.
又PA = AB，点F是PB的中点，
∴AF⊥PB，又PB∩BC=B，
∴AF⊥平面PBC ，又平面， ∴AF⊥PE. 所以，无论点E在边BC的何处，都有PE⊥AF.
4．（2021·贵州·高二学业考试）如图，在正方体中，为的中点.

（1）求证：平面；
（2）判断与平面的位置关系，并说明理由.
【答案】（1）证明见解析；（2）平面，理由见解析.
【分析】
（1）利用正方形的性质可得出，由正方体的几何性质以及线面垂直的性质可得出，利用线面垂直的判定定理可证得结论成立；
（2）设，连接，利用中位线的性质可得出，再利用线面平行的判定定理可得出结论.
【详解】
（1）四边形是正方形，，
在正方体中，平面，
平面，，
，因此，平面；
（2）平面，理由如下：
证明：设，连接，
、分别为、的中点，，
平面，平面，因此，平面.
5．（2021·四川自贡·三模（文））如图1，由正方形ABCD、直角三角形ABE和直角三角形CDF组成的平面图形，其中AB＝AE＝DF＝2，将图形沿AB、CD折起使得E、F重合于P，如图2．
（1）求四棱锥P﹣ABCD的体积；
（2）判断图2中平面PAB和平面PCD的交线l与平面ABCD的位置关系，并说明理由．
【答案】（1）；（2）l∥平面ABCD；答案见解析．
【分析】
（1）根据线面垂直的判定定理证出AB⊥平面PAD，进而可得平面PAD⊥平面ABCD，从而求出P到AD的距离即为四棱锥P﹣ABCD的高，再有锥体的体积公式即可求解.
（2）根据线面平行的判定定理可得AB∥平面PCD，再由线面平行的性质定理可得AB∥l，由线面平行的判定定理即可证明.
【详解】
解：（1）由图1可知，AB⊥AE，CD⊥DF，则图2中，AB⊥PA，AB⊥PD，
∵PA∩PD＝P，∴AB⊥平面PAD，而AB⊂平面ABCD，
∴平面PAD⊥平面ABCD，
又是边长为2的正三角形，
则P到AD的距离即为四棱锥P﹣ABCD的高，
∴；
（2）平面PAB和平面PCD的交线l∥平面ABCD．
理由如下：∵AB∥CD，AB⊄平面PCD，CD⊂平面PCD，
∴AB∥平面PCD，
AB⊂平面PAB，平面PAB∩平面PCD＝l，∴AB∥l，
而AB⊂平面ABCD，l⊄平面ABCD，
∴l∥平面ABCD．
6．（2021·江苏·高一专题练习）如图，已知三棱柱的侧棱与底面垂直，，、分别是、的中点．
（1）证明：；
（2）判断直线和平面的位置关系，并加以证明．【答案】（1）证明见解析；（2）平面，证明见解析．
【分析】
（1）由题意及线面垂直的定理和定义先证平面，再证出；
（2）判断出平面，设的中点为，连接、，证明出四边形为平行四边形，可得出，利用线面平行的判定定理可证得结论成立.
【详解】
（1）由题意知，平面，平面，，
，，平面，
平面，；
（2）平面.
证明如下：设的中点为，连接、．
、分别是、的中点，且，
又且，故四边形为平行四边形，所以，且，
为的中点，则且，所以，且，
故四边形为平行四边形，则，
平面，平面，故平面.
【点睛】
方法点睛：常见的线面平行的证明方法有：
（1）通过面面平行得到线面平行；
（2）通过线线平行得到线面平行，在证明线线平行中，经常用到中位线定理或平行四边形的性质.7．（2021·全国·高二专题练习）如图，正方体ABCD﹣A1B1C1D1中，M，N分别是AB，A1D1的中点.判断直线MN与平面BB1D1D的位置关系，并说明理由.
【答案】平行，理由见解析.
【分析】
根据题意可取AD中点E，连接ME，NE，根据题知MEBD，NED1D，可得平面EMN平面BB1D1D，即面面平行，利用面面平行即可证明线面平行.
【详解】
如图，MN平面BB1D1D，
取AD中点E，连接ME，NE，
根据题知MEBD，NED1D，
因为平面EMN， ME⊂平面EMN，
所以平面EMN，同理平面EMN，
又，所以平面EMN平面BB1D1D，
因为MN⊂平面EMN，
故MN平面BB1D1D.8．（2021·四川·石室中学高三期末（文））如图（1），在矩形中，，在边上，.沿，，将和折起，使平面和平面都与平面垂直，如图（2）.
（1）试判断图（2）中直线与的位置关系，并说明理由；
（2）若平面平面，证明平面.
【答案】（1），理由见解析；（2）证明见解析.
【分析】
（1）连结，分别取，的中点，，连结，，，则由题意可得，，，而平面和平面都与平面垂直，所以平面，平面，得，进而得四边形为平行四边形，再利用平行公理可证得结论；
（2）由线面平行的判定定理可得面，再利用线面平行的性质定理可得，而由（1）可得平面，所以平面
【详解】
（1）.理由如下：
连结，分别取，的中点，，连结，，，由图（1）
可得，与都是等腰直角三角形且全等，则，，
∵平面平面，交线为，平面，
∴平面.
同理得，平面，∴.
又∵∴四边形为平行四边形，
∴.
∵，分别是，的中点，∴
∴.（2）∵，平面，平面
∴面
∵平面，面平面
∴
由（1）知平面，
∴平面.
9．（2020·北京·高一期末）如图，在四棱锥中，底面ABCD是菱形，，平面ABCD，，，.
（1）求证：直线平面PNC；
（2）在AB上是否存在一点E，使平面PDE，若存在，确定E的位置，并证明，若不存在，说明理由；
（3）求三棱锥的体积.
【答案】（1）证明见解析；（2）E是AB中点，证明见解析；（3）.
【分析】
（1）在PC上取一点F，使，连接MF，NF，证明，，推出，即可得证；
（2）E是AB中点，证明，，利用线面垂直的判定定理即可证明平面PDE；
（3）证明为点到平面的距离，求出底面积，利用等体积法即可求解.
【详解】
（1）在PC上取一点F，使，连接MF，NF，因为，，所以，，，，
可得且.
所以MFNA为平行四边形，
即，
又平面，
所以直线平面.
（2）E是AB中点，证明如下：
因为E是AB中点，底面ABCD是菱形，，所以，
因为，所以， 即，
又平面ABCD，所以，
又，
所以直线平面PDE
（3）直线，且由（2）可知，DE为点A到平面PDC的距离，，
，
所以.
【点睛】
本题主要考查了直线与平面平行以及垂直的判断，考查了等体积法求三棱锥的体积，属于中档题.
10．（2020·福建·高二学业考试）如图，四棱锥中，底面是矩形，平面，且，．
（1）求四棱锥的体积；
（2）若分别是棱的中点，则与平面的位置关系是______，在下面三个选项中选取一个正确的序号填写在横线上，并说明理由．
①平面；
②平面；
③与平面相交．
【答案】（1）4；（2）②，理由见解析．
【分析】
（1）根据四棱锥体积公式直接计算；
（2）首先判断平面，要证明线面平行，需证明线线平行，取的中点，连接，．根据条件证明四边形是平行四边形.
【详解】
（1）因为平面，
所以．
（2）②，理由如下：
取的中点，连接，．
因为分别为，的中点，
所以，．
因为为的中点，所以，
又矩形中，，且，
所以，且，所以四边形是平行四边形．
所以．又平面，平面，
所以平面．
【点睛】
本题考查证明线面平行，几何体的体积，重点考查逻辑推理，空间想象能力，计算能力，属于基础题型.
11．（2021·广东·佛山一中高二期中）如图甲，直角梯形中，，，为中点，在上，且，已知，现沿把四边形折起（如图乙），使平面平面.
（1）求证：平面；
（2）求证：平面平面.
【答案】
（1）证明见解析；
（2）证明见解析.
【分析】
（1）根据线面平行的判定定理得出平面，同理平面，再根据面面平行的判定定理得出平面平面，最后由面面平行的性质从而可证出平面；
（2）根据题意，由面面垂直的性质得出，结合，再根据面面垂直的判定定理，即可证明平面平面.
（1）
证明：由题意知，平面，平面，
所以平面，同理平面，
∵，∴平面平面，
又平面，
∴平面.
（2）
证明：在图甲中，，，
∴，则在图乙中，，
又∵平面平面，平面平面，
∴平面，得，又∵，，∴平面，
而平面， ∴平面平面.
12．（2022·上海长宁·高二期末）在矩形中，是的中点，是上，，且，如图，将沿折起至：
（1）指出二面角的平面角，并说明理由；
（2）若，求证：平面平面；
（3）若是线段的中点，求证：直线平面；
【答案】
（1）为二面角的平面角，理由见解析
（2）证明见解析
（3）证明见解析
【分析】
（1）根据，结合二面角定义得到答案.
（2）证明平面得到，得到平面，得到证明.
（3）延长，交于点，连接，证明即可.
（1）
连接，则，，故为二面角的平面角.
（2），，，故平面，平面，
故，又，，故平面，
平面，故平面平面.
（3）
延长，交于点，连接，易知，故
故是的中点，是线段的中点，故，
平面，且平面，故直线平面.
13．（2021·辽宁大连·高三学业考试）如图，在四棱锥中，底面是边长为的菱形，，平面，、分别为、的中点.
（1）求三棱锥的体积；
（2）证明：平面.
【答案】（1）；
（2）证明见解析.
【分析】
（1）利用条件可得，结合棱锥的体积公式即求；
（2）取的中点，可证四边形为平行四边形，再利用线面平行的判定定理即证.
（1）
证明：设与的交点为，
因为底面是边长为的菱形，所以，且，
因为，所以，
在中，，故，
所以.
因为平面，所以为三棱锥的高，
所以三棱锥的体积.
（2）
取的中点，连接、，
因为为的中点，所以且，
又因为为的中点，四边形为菱形，所以且.
所以且.
故四边形为平行四边形，所以.因为平面，平面，所以平面.
14．（2021·四川·乐山市教育科学研究所一模（文））《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”.在如图所示的“阳马”中，侧棱底面，，点是的中点，作交于点.
（1）求证：平面；
（2）求证：平面.
【答案】
（1）证明见解析
（2）证明见解析
【分析】
（1）作出辅助线，利用中位线证明线线平行，进而证明线面平行；（2）由线面垂直得到线线垂直，进而证明线面垂直.
（1）
连接交于，连接，因为为矩形，所以为中点，又为中点，所以又平面，平面，所以平面.
（2）因为侧棱底面，平面，所以，
又为矩形，所以，，所以平面，平面，所以，因为为的中点，且，由三线合一得：，因为，所以平面，因为平面，从而，又，，所以平面.
15．（2022·全国·高三专题练习（文））如图，在四棱锥P—ABCD中，PA⊥平面ABCD，在直角梯形ABCD中，AD//BC，∠BAD=90°，BC=2AD，E为线段BC的中点．
（1）求证：平面PDE⊥平面PAD；
（2）在线段BD上是否存在点F，使得EF//平面PCD？若存在，求出点F的位置；若不存在，请说明理由；
（3）若AB=1，DC=，PA=2，求四棱锥P—ABCD的体积．
【答案】
（1）证明见解析；
（2）存在点F，F为BD的中点，理由见解析；
（3）1.
【分析】
（1）由题意，证明在平面PDE中的直线DE与平面PAD垂直即可；
（2）取BD的中点F，证明EF//CD即可；
（3）先求出底面直角梯形的面积，再利用锥体的体积公式即可求出四棱锥P—ABCD的体积.
（1）
证明：E为BC的中点，BC=2AD，
AD=BE，而AD//BC
四边形ABED是平行四边形，又∠BAD=90°，DE⊥AD，
又PA⊥平面ABCD，
DE⊥PA，PA∩AD=A
DE⊥平面PAD，而DE平面PDE，
平面PDE⊥平面PAD
（2）
解：存在点F，且F为BD的中点，理由如下：
取BD的中点F，如上图所示
E，F分别为BC，BD的中点，
EF//CD，而CD平面PCD，EF平面PCD，
EF//平面PCD
（3）
解：由条件可知BC=2，
所以梯形ABCD的面积为：
故四棱锥P-ABCD的体积为V=
16．（2021·全国·高二单元测试）如图，边长为2的正方形所在的平面与半圆弧所在平面垂直，是上异于，的点.
（1）证明：平面平面；
（2）在线段上是否存在点，使得平面，说明理由.
【答案】
（1）证明见解析
（2）存在，理由见解析
【分析】
（1）推导出平面，从而，推导出，从而平面，由此能证明平面平面；
（2）当为中点时，连结，，交于点，则是的中点，连结，推导出，从而平面．
（1）
证明：由题设知，平面平面， 平面平面，
，平面，平面，
平面，，
为上异于，的点，且为直径，，
又，平面，
平面，平面平面；
（2）
解：在线段上存在点，当为中点时，使得平面．
证明如下：
连结，，交于点，
是矩形，是的中点，连结，
是中点，，
平面，平面，平面，
所以当为中点时，平面．
17．（2021·宁夏·银川唐徕回民中学高二阶段练习）如图，直三棱柱中，，．
（1）求证：；
（2）在棱上是否存在点K，使得平面？若存在，求出的值；若不存在，请说明理由．
【答案】
（1）证明见解析
（2）当为中点时，平面，此时
【分析】
小问1：根据直三棱柱，得面面，结合，证明面，从而得到；
小问2：分别取，的中点为，，连接，证明，，进而证得面面，从而证得平面，得到的值.
（1）
因为为直三棱柱，故面面，
又面面，且，故面，又面，故
（2）
分别取，的中点为，，连接，
因为，故为的中位线，为的中位线，
因此，
又面，故面
又为直三棱柱，故，即，
又面，故面
又，故面面
又面，故平面，
此时
18．（2021·宁夏·银川市第六中学高二阶段练习）如图，在四棱锥中，平面，，.
（1）求证：平面.
（2）求证：平面平面.（3）设点为的中点，在棱上是否存在点，使得平面？说明理由.
【答案】
（1）证明见解析
（2）证明见解析
（3）为中点.证明见解析
【分析】
（1）证明，，得到平面.
（2）根据得到平面，得到证明.
（3）为中点时，平面，，平面，且平面，得到答案.
（1）
平面，平面，故，，，
故平面.
（2）
，平面，故平面，平面，故平面平面.
（3）
当为中点时，平面.
证明如下：为中点，为的中点，故，
平面，且平面，故平面.
19．（2021·陕西·西安中学高一阶段练习）如图所示，已知点P是平行四边形所在平面外一点，M，N，Q分别，，的中点，平面平面．
（1）证明平面平面；
（2）求证：．
【答案】
（1）证明见解析
（2）证明见解析
【分析】
（1）由线面平行、面面平行的判定即可证明.
（2）利用线面平行的性质定理即可证明.
（1）
证明：因为M，N，Q分别，，的中点，所以，
又平面ABCD,平面ABCD,
所以平面ABCD, 平面ABCD,
因为，平面MNQ,
所以平面平面，
（2）
证明：因为，平面，平面，
所以平面，
又平面平面，平面，所以.
20．（2021·黑龙江·哈尔滨三中高三阶段练习（理））如图，在四棱锥中，底面为直角梯形，，，，平面平面，，，分别为，的中点．
（1）求证：平面平面；
（2）求证：平面平面．
【答案】
（1）证明见解析
（2）证明见解析
【分析】
（1）由题意易知，平面，平面，根据面面平行的判定定理即可证出；
（2）根据平面知识可证，再根据面面垂直的性质定理可知平面，即可根据面面垂直的判定定理证出．（1）
因为，分别为，的中点，所以，又平面，平面，所以平面①；因为且，所以四边形为平行四边形，即有，又平面，平面，所以平面②，由①②及，平面，所以平面平面．
（2）
由（1）可知，，所以，即有，而平面平面，
平面平面，所以平面，而平面，所以平面平面．
21．（2021·山西吕梁·高三阶段练习（文））如图，在四棱锥中，底面直角梯形，，，是等边三角形，且，.
（1）设平面平面，求证：平面；
（2）若，求证：平面平面.
【答案】
（1）证明见解析；
（2）证明见解析.
【分析】
(1)利用线面平行的判定定理和性质即可证明；
(2)证明CD⊥AC，从而得到平面即可.
（1）
∵，平面，平面，∴∥平面，
又平面平面，平面，
∴，
又平面，平面，∴平面；
（2）
作，垂足为M，
∵，，∴，
又，，∴四边形为正方形，∴，
又，∴，∴，
又，∴，∴，
又，，，平面，∴平面，
∵平面，∴平面平面.
22．（2021·全国·高一单元测试）如图所示，已知多面体ABCDFE中，四边形ABCD为矩形，，，平面平面ABCD，O，M分别为AB，FC的中点．
（1）求证：；
（2）求证：平面DAF；
（3）若过EF的平面交BC于点G，交AD于点H，求证：．
【答案】
（1）证明见详解
（2）证明见详解
（3）证明见详解.
【分析】
（1）利用面面垂直的性质定理证出，再由线面垂直的判定定理证明平面，由线面垂直的性质定理即可证明.
（2）取的中点，连接，利用线面平行的判定定理即可证明.
（3）由面面平行的性质定理即可证明.
（1）
平面平面ABCD，
平面平面ABCD，
在矩形ABCD中，，平面 ABCD，
平面，，
又，，平面，平面，
平面，
（2）
取的中点，连接，
分别为的中点，
，且，，，
所以，且，
所以四边形为平行四边形，
所以，
平面DAF，平面DAF，
平面DAF.
（3）
，
过直线存在一个平面，
使得平面平面ABCD，
又过的平面交于，交于点，
平面ABCD，
，
23．（2020·广东揭东·高一期末）如图，在四棱锥中，平面，底面是菱形，，，，为与的交点，为棱上一点
（1）证明：平面；
（2）若平面，求三棱锥的体积.
【答案】
（1）证明见解析；
（2）.
【分析】
（1）根据菱形性质和线面垂直性质可得，，由线面垂直的判定可得结论；（2）连接，由线面平行性质可得，知为中点，由体积桥可得，根据长度关系可求得结果.
（1）
四边形为菱形，；
平面，平面，；
平面，，平面；
（2）
连接，
平面，平面，平面平面，，
又为中点，为中点，
四边形是菱形，，，，；
由（1）知：平面，
.
24．（2021·全国·高一课时练习）在三棱柱中，
（1）若分别是的中点，求证：平面平面.
（2）若点分别是上的点，且平面平面，试求的值．【答案】（1）证明见解析；（2）1.
【分析】
（1）先证明平面，在证明平面，即可证明平面平面；
（2）连接交于O，连接，由题意先面面平行的性质证明，再由平行的性质结合题设即可求解
【详解】
（1）∵分别是的中点，
∴，
∵平面，平面，
∴平面，
∵，，
∴四边形是平行四边形，
∴，
又∵平面，平面，
∴平面，
又∵，平面，
∴平面平面；
（2）连接交于O，连接，
由平面平面，且平面平面，
平面平面，∴，
则，
又由题设，∴，即.
25．（2021·上海浦东新·高二期中）已知是矩形所在平面外一点，，分别是，的中点，求证：平面.
【答案】证明见解析
【分析】
解法1：取中点，连接，，由三角形中位线定理结合已知条件可得四边形是平行四边形，从而得，再利用线面平行的判定定理可证得结论，
解法2：取中点，连接，，则由三角形中位线定理和平行四边形的性质可得，，再由面面平行的判定定理可得平面平面，然后由面面平行的性质可得结论
【详解】
解法（1）取中点，连接，，
是中点，是中点，，，
是矩形边中点，，，
，，所以四边形是平行四边形，
，且是平面外的一条直线，是平面上的一条直线，
平面.
解法（2）取中点，连接，，
是中点，是中点，所以，
因为是的中点，是的中点，
所以,因为，，
所以， ,
所以四边形为平行四边形
所以，
因为平面，平面，平面，平面，
所以平面，平面，
因为
所以平面平面，
因为平面，所以平面.
26．（2021·全国·高一课前预习）如图，平面平面，四边形为矩形，和均为等腰直角三角形，且.
（1）求证：平面平面；
（2）若点为线段上任意一点，求证：平面.
【答案】（1）证明见解析；（2）证明见解析.
【分析】
（1）证明出平面，可得出，由已知条件得出，利用线面垂直、面面垂直的判定定理可证得结论成立；（2）证明出平面平面，再利用面面平行的性质可证得平面.
【详解】
（1）因为为矩形，所以，
又因为平面平面，平面，平面平面，所以平面，
又因为平面，所以，
因为，即，且、平面，，
所以平面.
又因为平面，所以平面平面；
（2）因为，平面，平面，所以平面.
因为和均为等腰直角三角形，且，
所以，所以，
又平面，平面，所以平面，
因为，所以平面平面.
又因为平面，所以平面.
27．（2021·全国·高二课时练习）如图，在直三棱柱中，，，点D，E，F分别为棱，，的中点．求证：
(1)平面DEF；
(2)平面平面DEF．
【答案】(1)证明见解析；(2)证明见解析.
【分析】
(1)首先证明平面平面，然后利用面面平行的性质即可证明线面平行；(2)首先利用正方形性质证明，然后利用线面垂直判定定理和性质证明，进而证明平面，最后利用面面垂直的判定定理即可求解.
【详解】(1)连接，如下图：
因为点D，E，F分别为棱，，的中点，几何体为直三棱柱，
所以，，
又因为，，，平面；，平面，
所以平面平面，
又因为平面，
所以平面.
(2) 因为，几何体为直三棱柱，
所以四边形为正方形，故，
因为，所以，
又因为，，，所以平面，
又因为平面，所以，
又因为，所以平面，
又因为平面，所以平面平面.
28．（2022·全国·高三专题练习）如图，四棱台中，底面为直角梯形，，， ，为棱的中点，证明：平面.
【答案】证明见解析
【分析】
延长CC1，BB1交于点V，在BB1上取点Q，使，再连BD交AC于点O，连接OQ，证明，即可推理作答.
【详解】
在四棱台中，在BB1上取点Q，使，连BD交AC于点O，连接OQ，如图，
延长CC1，BB1交于点V，由，则，，
则，即，又平面，平面，于是得平面，
在直角梯形中，，则，于是得，又平面，平面，则平面，
又，平面OQC，因此得平面平面OQC，又平面OQC，
所以平面.
29．（2022·全国·高三专题练习）如图，在多面体中，是矩形，是正方形，点为的中点，求证：平面.
【答案】证明见解析
【分析】
连AC交BD于点N，连MN，证明MN，BN都平行于平面EFC，再经推理论证即可作答.
【详解】
连接AC交BD于点N，连接MN，如图，
因四边形ABCD是正方形，则N为AC的中点，而M为AE的中点，于是得MN//CE，
又平面EFC，平面EFC，因此，MN//平面EFC，
在矩形中，，平面EFC，平面EFC，则BN//平面EFC，
而，平面BMN，从而得平面BMN//平面EFC，又平面BMN，
所以BM//平面EFC.
30．（2021·河南·高三阶段练习（文））如图所示，在四棱锥中，，，为等边三角形，且平面ADE平面BCDE，F为棱AC的中点．
（1）求四棱锥的体积；
（2）证明：．【答案】
（1）；
（2）证明见解析.
【分析】
(1)根据给定条件求出等腰梯形的面积，取DE中点O，连AO，证得平面即可计算作答.
(2)利用(1)中信息，证得平面，连FG，再证平面即可推理作答.
（1）
因，，则四边形是等腰梯形，取CD中点G，连BG，如图，
显然有，，则四边形是平行四边形，，
于是得是正三角形，等腰梯形的高等于正的高，
等腰梯形的面积，
取DE中点O，连AO，为等边三角形，则，而平面ADE平面BCDE，
平面ADE，平面ADE平面，因此，平面，又，
从而有，
所以四棱锥的体积是.
（2）
由(1)知，，，
在中，，
于是得，即，即有，
又平面，平面，则，而，平面，
因此有平面，而平面，则，
连FG，因F为棱AC的中点，G为CD的中点，则，于是得，
又，平面，从而得平面，因平面，所以.
31．（2021·河南·温县第一高级中学高三阶段练习（文））如图，直四棱柱中，上下底面为等腰梯形，．，，为线段的中点．
（1）证明：平面平面；
（2）设为线段上一点，试确定点的位置，使平面平面．
【答案】
（1）证明见解析；
（2）点为中点.
【分析】
(1)根据给定条件可得，利用勾股定理证明即可证得平面平面.
(2)取的中点，证明和，利用面面平行的判定定理即可推理作答.
（1）
因为为直四棱柱，则平面，而平面，于是得，
在中，，，由余弦定理得，，
因此，，即，又，平面，则平面，又平面，
所以平面平面.
（2）
当点为中点时，平面平面，
连接，如图，
在等腰梯形中，，
即，而，则四边形为平行四边形，即有，
因平面，平面，则有平面，
因为，，则四边形为平行四边形，有，而平面，平面，
因此，平面，又，
所以平面平面.
32．（2021·贵州·高三阶段练习（文））如图，在四棱锥中，已知，，，，且平面.
（1）证明：平面平面.
（2）若是上一点，且平面，求三棱锥的体积.
【答案】
（1）证明见解析
（2）
【分析】
（1）利用线面垂直证明面面垂直；
（2）设过点和的平面交平面于，根据线面平行的性质定理可证为平行四边形，进而可得及三棱锥体积.
（1）
证明：因为，，所以，
因为平面，所以，
又，所以平面，
因为平面，
所以平面平面；
（2）
解：如图，设过点和的平面交平面于，点在上，连接因为平面，则，
因为，且平面，所以平面，
又平面平面，所以.
所以四边形为平行四边形，则.
过点作，垂足为，则平面.
又，，可得，
所以.
33．（2021·贵州毕节·模拟预测（文））如图1，正方形中，，，将四边形沿折起到四边形的位置，使得(如图2)．
（1）证明：平面平面；
（2）若分别为的中点，求三棱锥的体积．
【答案】
（1）见解析；
（2）﹒
【分析】
（1）证明QM⊥AQ和QM⊥QP结合线面垂直、面面垂直的判定即可得证；
（2）根据几何关系，利用，由锥体体积公式即可得解.
（1）
∵在正方形中，，，
∴QM⊥QP，，
又∵∠AMQ＝60°，∴在△AMQ中，由余弦定理得，
，
，
，
又∵平面ABPQ，∴平面ABPQ，
又∵QM平面MNPQ，∴平面平面；
（2）由（1）知AQ⊥QM，QM⊥QP，
∵在正方形中，，，
∴四边形CDMN为矩形
∴MN⊥AM，MN⊥DM，
∴MN⊥MQ，MN⊥MA，
∵MQ∩MA＝M，MQ、MA平面AMQ，∴MN⊥平面AMQ，
∵MN平面ABNM，∴平面ABNM⊥平面AMQ，
过Q作QH⊥AM于H，则QH⊥平面ABNM，即QH⊥平面BEF，
QH＝QMsin60°＝，
∴﹒
34．（2021·四川·凉山彝族自治州教育科学研究所一模（文））图1是，，，、分别是边、上的两点，且，将沿折起使得，如图2.
（1）证明：图2中，；
（2）图2中，求三棱锥的体积.
【答案】（1）证明见解析；
（2）.
【分析】
（1）证明得出平面，利用线面垂直的性质可证得结论成立；
（2）证明出平面，计算出的面积，利用锥体的体积公式可求得结果.
（1）
证明：在图1中，因为，则，，则，
在图（2）中，则有，，，则平面，
平面，因此，.
（2）
解：在图1中，因为，则，，
在图2中，平面，，则平面，
因为，则，
故.
35．（2021·广西玉林·模拟预测（文））如图所示的四棱锥中，底面为正方形，平面平面，，，分别是，，的中点，，．
（1）求证：平面；
（2）求三棱锥的体积．
【答案】
（1）证明见解析；
（2）.【分析】
(1)根据给定条件证得及即可推理作答.
(2)由给定条件可得点到平面的距离是点到平面的距离的，再借助三棱锥等体积法转化求解即得.
（1）
在中，，为的中点，则，又平面平面，
平而平面，平而，于是得平面，
而平面，则，又底面是正方形，，分别是，的中点，即，
因，平面，
所以平而.
（2）
因为的中点，则点到平面的距离是点到平面的距离的，如图，
因此，，
所以三棱锥的体积为.
36．（2019·广东·顺德一中高二期中）如图，在四棱锥中，，，，平面平面，，是的中点.求证：
（1）底面；
（2）平面．
【答案】
（1）证明见解析.
（2）证明见解析.
【分析】
（1）根据面面垂直的性质定理，即可得证；
（2）根据已知条件可证，再由线面平行的判定定理，即可证明结论.
（1）
证明：因为平面PAD⊥底面ABCD，且，平面 底面ABCD，
所以PA⊥底面ABCD.
（2）
证明：因为AB∥CD，CD＝2AB，E为CD的中点，所以AB∥DE，且AB＝DE，
所以四边形ABED为平行四边形，所以BE∥AD.
又因为BE⊄平面PAD，AD⊂平面PAD，
所以BE∥平面PAD.
37．（2021·黑龙江·大庆中学高三期中（文））如图，在三棱柱中，平面平面，是的中点．
（1）证明：；
（2）求三棱锥的体积．
【答案】
（1）证明见解析.
（2）.
【分析】
（1）连接，由平面几何知识证得，根据面面垂直的性质可证得，再由线面垂直的判定和性质可得证；
（2）运用等体积法可求得三棱锥的体积．
（1）
证明：在三棱柱中，连接，
，，，
是等边的边的中点，，
平面平面，平面平面，所以平面，，
又平面，.（2）
（2）由（1）知平面，
.
38．（2021·四川·高三阶段练习（文））如图，在四棱锥中，平面，底面为直角梯形，，，且，，为的中点．
（1）证明：平面．
（2）过，，作四棱锥的截面，请写出作法和理由，并求截面的面积．
【答案】
（1）证明见解析
（2）作法和理由见解析；面积
【分析】
（1）由平面，得到,再由，证得，利用线面垂直的判定定理，证得平面，得到，结合，进而证得平面．
（2）过作，交于，连接，证得，得到过，，的截面为四边形，由（1）知证得，结合直角梯形的面积公式，即可求解.
（1）证明：因为平面，平面，所以,
又因为，，所以，
由且平面，所以平面，
又由平面，所以，
因为，为的中点，所以，
又因为且平面，所以平面．
（2）
解：如图所示，过作，交于，连接，则截面为四边形．
理由如下：
因为，，所以，所以，，，四点共面，
所以过，，的截面为四边形，
由（1）知平面，因为平面，所以，
又由，
所以四边形为直角梯形，其面积．
39．（2021·云南·高三阶段练习（文））已知ABCD是边长为2的正方形，平面平面DEC，直线AE，BE与平面DEC所成的角都为45°.
（1）证明：.
（2）求四棱锥E-ABCD的体积V.
【答案】
（1）证明见解析
（2）
【分析】
（1）已知平面平面DEC，，由面面垂直的性质定理即可证得线面垂直，进而证得结果；
（2）根据已知可求得.取CD的中点O，连接OE，可证得平面ABCD，根据四棱锥E-ABCD的体积.即可求得结果.
（1）
（1）证明：因为ABCD是正方形，所以.
因为平面平面DEC，平面平面，
所以平面DEC，
又平面DEC，所以.
（2）
解：因为，所以平面DEC，则和分别是直线AE，BE与平面DEC所成的角，即，
所以.取CD的中点O，连接OE，所以.
因为平面平面DEC，平面平面，所以平面ABCD，即OE为四棱锥E-ABCD的高，且.
所以四棱锥E-ABCD的体积.