新高考数学一轮复习学案第23讲 立体几何小题（2份打包，原卷版+解析版）

这是一份新高考数学一轮复习学案第23讲 立体几何小题（2份打包，原卷版+解析版），文件包含新高考数学一轮复习学案第23讲立体几何小题原卷版doc、新高考数学一轮复习学案第23讲立体几何小题解析版doc等2份试卷配套教学资源，其中试卷共56页， 欢迎下载使用。
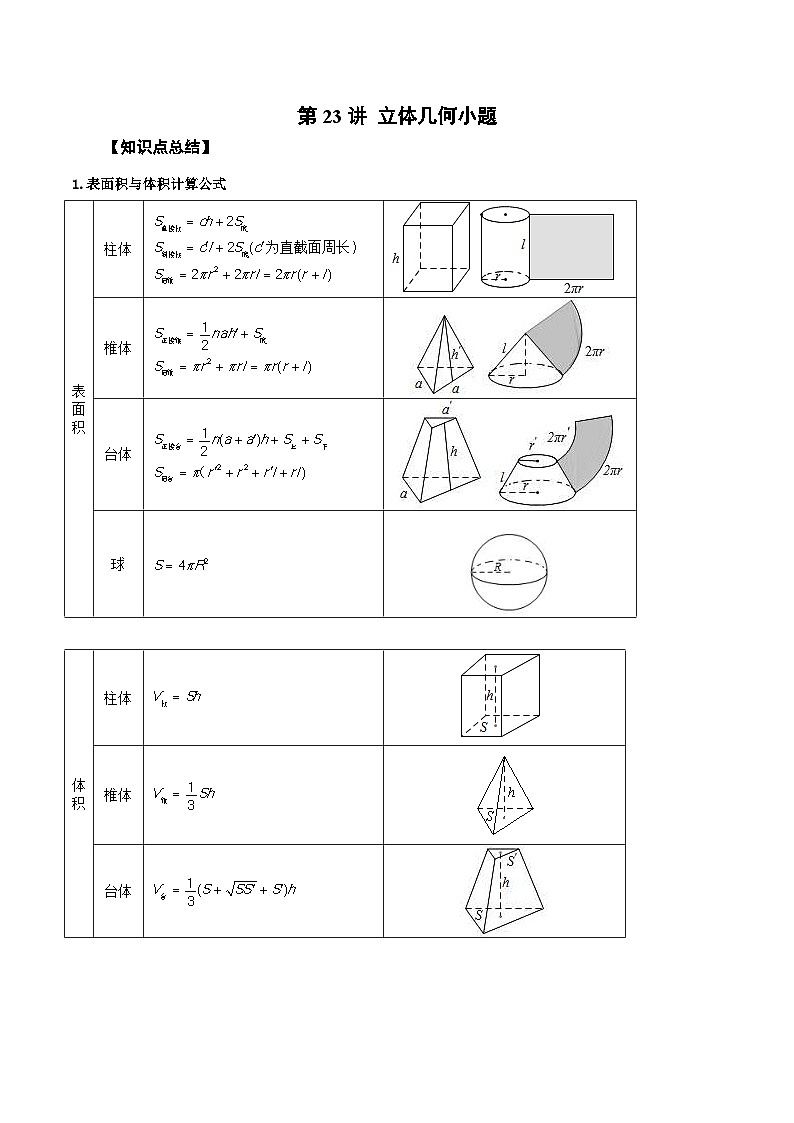
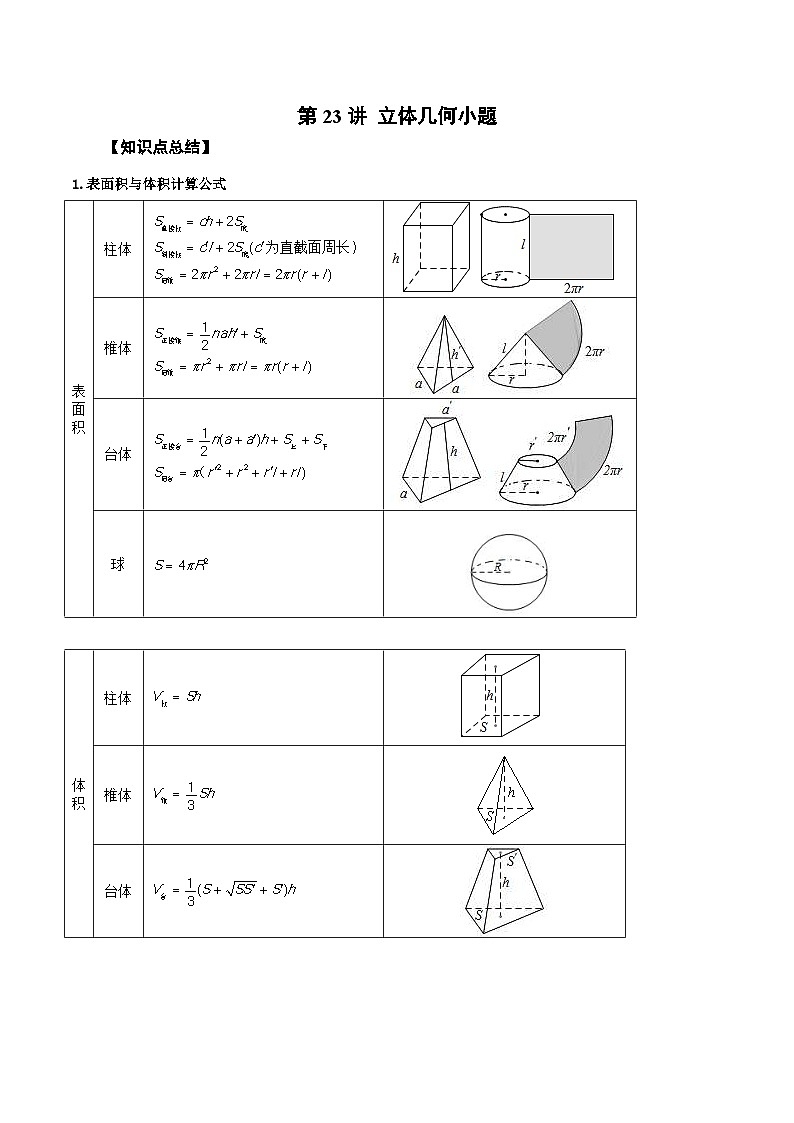
1.表面积与体积计算公式
表面积
柱体
SKIPIF 1 < 0
SKIPIF 1 < 0 为直截面周长 SKIPIF 1 < 0
SKIPIF 1 < 0
椎体
SKIPIF 1 < 0
SKIPIF 1 < 0
台体
SKIPIF 1 < 0
SKIPIF 1 < 0
球
SKIPIF 1 < 0
体积
柱体
SKIPIF 1 < 0
椎体
SKIPIF 1 < 0
台体
SKIPIF 1 < 0
2.斜二测画法
斜二测画法的主要步骤如下:
(1)建立直角坐标系.在已知水平放置的平面图形中取互相垂直的 SKIPIF 1 < 0 ,建立直角坐标系.
(2)画出斜坐标系.在画直观图的纸上(平面上)画出对应图形.在已知图形平行于 SKIPIF 1 < 0 轴的线段,在直观图中画成平行于 SKIPIF 1 < 0 使 SKIPIF 1 < 0 (或 SKIPIF 1 < 0 ),它们确定的平面表示水平平面.
(3)画出对应图形.在已知图形平行于 SKIPIF 1 < 0 轴的线段,在直观图中画成平行于 SKIPIF 1 < 0 轴的线段,且长度保持不变;在已知图形平行于 SKIPIF 1 < 0 轴的线段,在直观图中画成平行于 SKIPIF 1 < 0 轴,且长度变为原来的一般.可简化为“横不变,纵减半”.
(4)擦去辅助线.图画好后,要擦去 SKIPIF 1 < 0 轴、 SKIPIF 1 < 0 轴及为画图添加的辅助线(虚线).被挡住的棱画虚线.
注: 直观图和平面图形的面积比为 SKIPIF 1 < 0 .
3.外接球与内切球
类型1：正方体或长方体外接球的球心在其体对角线的中点。
类型2：正棱柱或直棱柱(圆柱)的球心在上下底面外心连线中点处。
推论：垂面模型（一条直线垂直于一个平面）可补成直三菱柱或长方体。
公式： SKIPIF 1 < 0 ,（R为外接球半径，r为底面外接圆半径，h为棱锥的高，r可根据正弦定理 SKIPIF 1 < 0
类型3：正棱锥（圆锥）模型(侧棱相等，底面为正多边形）的球心在其顶点与底面外心连线线段(或延长线）上。
半径公式： SKIPIF 1 < 0 （R为外接球半径，r为底面外接圆半径，h为棱锥的高，r可根据正弦定理 SKIPIF 1 < 0
类型4：若棱锥的顶点可构成共斜边的直角三角形，则公共斜边的中点就是其外接球的球心。
类型5：锥体的内切球问题
三棱锥 SKIPIF 1 < 0 是任意三棱锥，求其的内切球半径
方法：等体积法，即内切球球心与四个面构成的四个三棱锥的体积之和相等
第一步：先画出四个表面的面积和整个锥体体积；
第二步：设内切球的半径为 SKIPIF 1 < 0 ，建立等式： SKIPIF 1 < 0 SKIPIF 1 < 0
SKIPIF 1 < 0
第三步：解出 SKIPIF 1 < 0
球
SKIPIF 1 < 0
【典型例题】
例1．（2015·吉林长春·高三阶段练习（文））已知一个四面体的所有棱长都为2,则该四面体的外接球表面积为________.
例2．（2015·吉林长春·高三阶段练习（理））已知三棱锥 SKIPIF 1 < 0 中, SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 .则该三棱锥的外接球表面积为________.
例3．（2022·全国·高三专题练习（理））若棱长为 SKIPIF 1 < 0 的正方体内部有一个球，球与正方体的各个面相切（即正方体的内切球）则该球的表面积为_____________．
例4．（2022·全国·高三专题练习）已知正方体的棱长为2，则与正方体的各棱都相切的球的表面积是_______．
例5．（2022·全国·高三专题练习（理））已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是两条不同的直线， SKIPIF 1 < 0 ， SKIPIF 1 < 0 是两个不同的平面，下列说法：
①若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 可能平行；
②若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 可能相交､平行或异面；
③若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 一定垂直；
④若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 一定平行.
以上说法正确的是___________.（填序号）
例6．（2022·全国·高三专题练习）已知 SKIPIF 1 < 0 是不重合的两条直线， SKIPIF 1 < 0 为不重合的两个平面，给出下列命题：
①若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ；
②若 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ；
③若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ．
所有正确命题的序号为__．
例7．（2022·上海·高三专题练习）有一块四边形的菜地，它的水平放置的平面图形的斜二测直观图是直角梯形，如图所示， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则这块菜地的面积为___________.
【技能提升训练】
一、单选题1．（2021·全国·高三专题练习（文））四面体 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 面 SKIPIF 1 < 0 ，则四面体 SKIPIF 1 < 0 的外接球表面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
2．（2021·全国·高三专题练习）在直三棱柱 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，若该直三棱柱的外接球表面积为 SKIPIF 1 < 0 ，则此直三棱柱的高为（ ）．
A．4B．3C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3．（2021·江西上饶·高二阶段练习（理））三棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 平面ABC，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，三棱锥 SKIPIF 1 < 0 的外接球表面积为（ ）
A．16πB．20πC． SKIPIF 1 < 0 D．24π
4．（2021·全国·高三专题练习（文））已知长方体的两个底面是边长为 SKIPIF 1 < 0 的正方形，长方体的一条体对角线与底面成 SKIPIF 1 < 0 角，则此长方体的外接球表面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
5．（2021·全国·高三期末（文））如图，在直三棱柱 SKIPIF 1 < 0 的侧面展开图中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 是线段 SKIPIF 1 < 0 的三等分点，且 SKIPIF 1 < 0 ．若该三棱柱的外接球 SKIPIF 1 < 0 的表面积为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
6．（2021·全国·高三专题练习）已知三棱锥 SKIPIF 1 < 0 中，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 和 SKIPIF 1 < 0 都是边长为2的等边三角形，则该三棱锥的外接球表面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
7．（2021·全国·高三专题练习）四面体 SKIPIF 1 < 0 中， SKIPIF 1 < 0 底面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则四面体 SKIPIF 1 < 0 的外接球表面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
8．（2021·全国·高三专题练习）已知直三棱柱 SKIPIF 1 < 0 的顶点都在球 SKIPIF 1 < 0 上，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则此直三棱柱的外接球 SKIPIF 1 < 0 的表面积是（ ）A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
9．（2020·内蒙古赤峰·高三阶段练习（文））据《九章算术》记载，“鳖臑(biēnà)”为四个面都是直角三角形的三棱锥.如图所示，现有一个“鳖臑”， SKIPIF 1 < 0 底面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，三棱锥外接球表面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
10．（2022·全国·高三专题练习）如图，三棱锥 SKIPIF 1 < 0 的四个顶点恰是长、宽、高分别是m，2，n的长方体的顶点，此三棱锥的体积为2，则该三棱锥外接球体积的最小值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
11．（2019·江西省抚州市第一中学高三期末（文））在三棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则三棱锥 SKIPIF 1 < 0 的外接球表面积是
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
12．（2020·全国·高三专题练习（理））在长方体 SKIPIF 1 < 0 中，四边形 SKIPIF 1 < 0 是边长为2的正方形， SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成的角是 SKIPIF 1 < 0 ，则长方体的外接球表面积是
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
13．（2019·安徽安庆·高三期末（理））正三棱柱 SKIPIF 1 < 0 中，底面边长 SKIPIF 1 < 0 ，侧棱长 SKIPIF 1 < 0 ，则该棱柱的外接球表面积等于
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0 14．（2014·全国·一模（文））正方体内切球和外接球半径的比为
A．
B．
C．
D．1:2
15．（2016·河北武邑·高三期末（理））正三角形的边长为，将它沿高翻折，使点与点间的距离为，此时四面体外接球表面积为
A．B．C．D．
16．（2016·云南玉溪·三模（文））已知三棱锥 SKIPIF 1 < 0 的外接球为球 SKIPIF 1 < 0 ，球 SKIPIF 1 < 0 的直径 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 都是等边三角形，则三棱锥 SKIPIF 1 < 0 的体积是
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
17．（2021·山西运城·高三开学考试（文））在三棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则三棱锥 SKIPIF 1 < 0 外接球的表面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
18．（2021·全国全国·模拟预测）若一个圆柱的内切球（与圆柱的两底面以及每条母线均相切）的表面积为 SKIPIF 1 < 0 ，则这个圆柱的体积为（ ）
A． SKIPIF 1 < 0 B．2C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
19．（2021·全国·高三专题练习（文））如图所示是古希腊数学家阿基米德的墓碑文，墓碑上刻着一个圆柱，圆柱内有一个内切球，这个球的直径恰好与圆柱的高相等，相传这个图形表达了阿基米德最引以为自豪的发现，我们来重温这个伟大发现，圆柱的表面积与球的表面积之比为（ ）
A． SKIPIF 1 < 0 B．2C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
20．（2022·全国·高三专题练习）蹴鞠(如图所示)，又名蹴球､蹴圆､筑球､踢圆等，蹴有用脚蹴､踢的含义，鞠最早系外包皮革､内实米糠的球.因而蹴鞠就是指古人以脚蹴､塌､踢皮球的活动，类似今日的足球.2006年5月20日，蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗传名录.已知某蹴鞠内切于三棱锥 SKIPIF 1 < 0 ， SKIPIF 1 < 0 面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则该蹴鞠的体积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
21．（2021·天津市新华中学高三阶段练习）已知正方体的内切球(球与正方体的六个面都相切)的体积是 SKIPIF 1 < 0 ，则该正方体的表面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
22．（2022·全国·高三专题练习）如图，在下列四个正方体中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 为正方体的两个顶点， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 为所在棱的中点，则在这四个正方体中，直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 不平行的是（ ）
A．B．C．D．
23．（2022·上海·高三专题练习）一个水平放置的平面图形的直观图是一个底角为45°，腰和上底长均为1的等腰梯形，则该平面图形的面积等于（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
24．（2022·上海·高三专题练习）如图， SKIPIF 1 < 0 是 SKIPIF 1 < 0 的斜二测直观图，其中 SKIPIF 1 < 0 ，斜边 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的面积是（ ）
A． SKIPIF 1 < 0 B．1C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
25．（2022·全国·高三专题练习）已知三条不同的直线 SKIPIF 1 < 0 和两个不同的平面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则下列四个命题正确的是（ ）
A．若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 B．若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 C．若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 D．若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
26．（2022·全国·高三专题练习）若a､b､c是空间三条不同的直线，则下列命题正确的是（ ）
A．若 SKIPIF 1 < 0 ，则a､b､c共面B．若a､b､c过同一点，则a､b､c共面
C．若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 D．若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
27．（2022·全国·高三专题练习）设 SKIPIF 1 < 0 为不重合的平面， SKIPIF 1 < 0 为不重合的直线，则其中正确命题的序号为（ ）
① SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ；② SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ；③ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ；④ SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
A．①③B．②③C．②④D．③④
28．（2022·全国·高三专题练习）设 SKIPIF 1 < 0 是一条直线， SKIPIF 1 < 0 ， SKIPIF 1 < 0 是两个平面，下列结论正确的是（ ）
A．若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 B．若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
C．若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 D．若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
29．（2022·全国·高三专题练习）如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则（ ）
A．BM＝EN，且直线BM，EN是相交直线
B．BM≠EN，且直线BM，EN是相交直线
C．BM＝EN，且直线BM，EN是异面直线
D．BM≠EN，且直线BM，EN是异面直线
30．（2022·全国·高三专题练习）底面为正三角形的直棱柱ABC﹣A1B1C1中，AB＝8，AA1＝6，M，N分别为AB，BC的中点，则异面直线A1M与B1N所成的角的余弦值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
31．（2022·全国·高三专题练习）在正方体 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的中点，则直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成角的大小是（ ）．
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
32．（2022·上海·高三专题练习）设 SKIPIF 1 < 0 ､ SKIPIF 1 < 0 为两条直线， SKIPIF 1 < 0 ､ SKIPIF 1 < 0 为两个平面，则下列命题中假命题是（ ）
A．若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
B．若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
C．若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
D．若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
33．（2022·全国·高三专题练习）已知 SKIPIF 1 < 0 为异面直线， SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ．直线 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0 且 SKIPIF 1 < 0
B． SKIPIF 1 < 0 且 SKIPIF 1 < 0
C． SKIPIF 1 < 0 与 SKIPIF 1 < 0 相交，且交线垂直于 SKIPIF 1 < 0
D． SKIPIF 1 < 0 与 SKIPIF 1 < 0 相交，且交线平行于 SKIPIF 1 < 0
34．（2022·全国·高三专题练习）下列命题中错误的是（ ）
A．如果平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，那么平面 SKIPIF 1 < 0 内一定存在直线平行于平面 SKIPIF 1 < 0
B．如果平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，那么平面 SKIPIF 1 < 0 内所有直线都垂直于平面 SKIPIF 1 < 0
C．如果平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，那么 SKIPIF 1 < 0 平面 SKIPIF 1 < 0
D．如果平面 SKIPIF 1 < 0 不垂直于平面 SKIPIF 1 < 0 ，那么平面 SKIPIF 1 < 0 内一定不存在直线垂直于平面 SKIPIF 1 < 0
35．（2022·上海·高三专题练习）已知直二面角 SKIPIF 1 < 0 ，直线 SKIPIF 1 < 0 在平面 SKIPIF 1 < 0 上，直线 SKIPIF 1 < 0 在平面 SKIPIF 1 < 0 上，且直线 SKIPIF 1 < 0 与直线 SKIPIF 1 < 0 不垂直，直线 SKIPIF 1 < 0 与直线 SKIPIF 1 < 0 不垂直，则以下判断正确的是（ ）
A． SKIPIF 1 < 0 与 SKIPIF 1 < 0 可能垂直，但不可能平行
B． SKIPIF 1 < 0 与 SKIPIF 1 < 0 可能垂直，也可能平行
C． SKIPIF 1 < 0 与 SKIPIF 1 < 0 不可能垂直，但可能平行
D． SKIPIF 1 < 0 与 SKIPIF 1 < 0 不可能垂直，也不可能平行
36．（2022·全国·高三专题练习）在正方体 SKIPIF 1 < 0 中P，Q分别是 SKIPIF 1 < 0 和 SKIPIF 1 < 0 的中点，则下列判断错误的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 平面 SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0 平面 SKIPIF 1 < 0 37．（2022·全国·高三专题练习）如图所示，在四边形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，将 SKIPIF 1 < 0 沿 SKIPIF 1 < 0 折起，使得平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，构成四面体 SKIPIF 1 < 0 ，则下列说法正确的是（ ）
A．平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 B．平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0
C．平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 D．平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0
二、填空题
38．（2021·黑龙江·佳木斯一中高三阶段练习（理））在直三棱柱 SKIPIF 1 < 0 中， SKIPIF 1 < 0 .若该直三棱柱的外接球表面积为 SKIPIF 1 < 0 ，则此三棱柱的高为__________.
39．（2022·全国·高三专题练习）已知在四面体 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，则四面体 SKIPIF 1 < 0 的外接球表面积为______.
40．（2022·全国·高三专题练习）正六棱柱的底面边长为4，高为6，则它的外接球(正六棱柱的顶点都在此球面上)的表面积为____．
41．（2021·广西柳州·高三开学考试（文））已知长方体 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则该长方体的外接球（长方体的八个顶点都在球面上）的表面积等于___________.
42．（2022·全国·高三专题练习（理））若球О是直三棱柱 SKIPIF 1 < 0 的外接球，三棱柱的高和体积都是4，底面是直角三角形，则球О表面积的最小值是___________.
43．（2021·甘肃白银·模拟预测（理））已知四棱锥 SKIPIF 1 < 0 的底面 SKIPIF 1 < 0 是矩形，其中 SKIPIF 1 < 0 ，侧棱 SKIPIF 1 < 0 底面 SKIPIF 1 < 0 ，且直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成角的余弦值为 SKIPIF 1 < 0 ，则四棱锥 SKIPIF 1 < 0 的外接球表面积为___________.
44．（2020·重庆市第二十九中学校高三阶段练习）已知某圆柱的侧面积为 SKIPIF 1 < 0 ，当此圆柱的外接球体积最小时，它的高为________.
45．（2021·全国·高三专题练习）已知正三棱柱 SKIPIF 1 < 0 的体积为54， SKIPIF 1 < 0 ，记三棱柱 SKIPIF 1 < 0 的外接球为球 SKIPIF 1 < 0 ，则外接球 SKIPIF 1 < 0 的表面积是__________．
46．（2019·全国·高三专题练习）已知棱长为 SKIPIF 1 < 0 的正方体的外接球表面积等于内切球体积的6倍，则实数 SKIPIF 1 < 0 ________．47．（2019·天津·二模（文））球__________．
48．（2021·宁夏·六盘山高级中学一模（文））三棱锥 SKIPIF 1 < 0 中， SKIPIF 1 < 0 面 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则三棱锥 SKIPIF 1 < 0 的外接球表面积为________.