






新高考数学一轮复习课件第2章函数导数及其应用第9讲 函数模型及其应用(含解析)
展开1.常见的几种函数模型
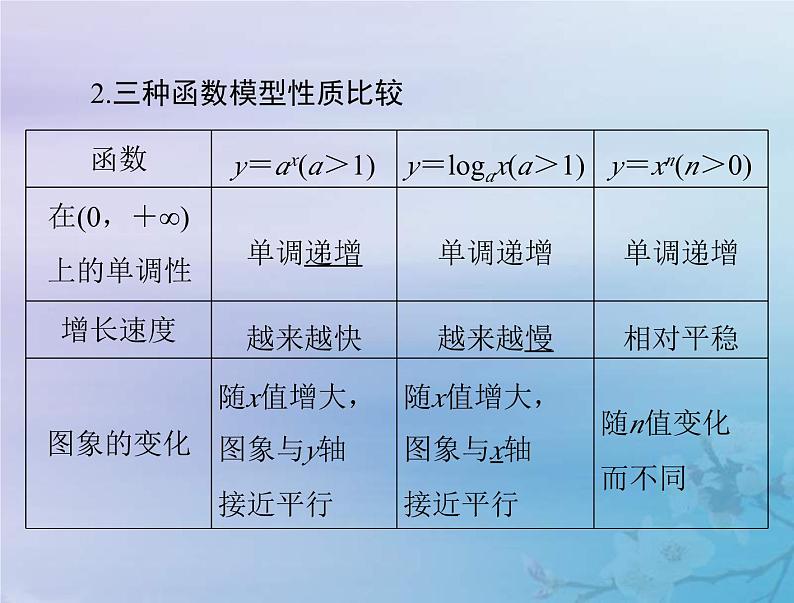
2.三种函数模型性质比较
(1)“直线上升”是匀速增长,其增长量固定不变;“指数增长”先慢后快,其增长量成倍增加,常用“指数爆炸”来形容;“对数增长”先快后慢,其增长速度缓慢.(2)易忽视实际问题中自变量的取值范围,需合理确定函数的定义域,必须验证数学结果对实际问题的合理性.
1.(多选题)下列结论错误的是(
A.函数y=2x的函数值比y=x2的函数值大B.“指数爆炸”是指数型函数 y=a·bx+c(a≠0,b>0,b≠1)增长速度越来越快的形象比喻C.幂函数增长比直线增长更快
题组二 走进教材2.(教材改编题)某家具的标价为 132 元,若降价以九折出售(即优惠 10%),仍可获利 10%(相对进货价),则该家具
B.105 元D.108 元
的进货价是(A.118 元C.106 元答案:D
3.(教材改编题)在某个物理实验中,测得变量 x 和变量y 的几组数据,如下表:
则对 x,y 最适合的拟合函数是(
B.y=x2-1D.y=lg2x
A.y=2xC.y=2x-2
题组三 真题展现4.(2020 年全国Ⅲ)Lgistic 模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数 I(t)(t 的单位:天)的 Lgistic
=0.95K 时,标志着已初步遏制疫情,则 t*约为(ln 19≈3)
5.(2021 年北京)对 24 小时内降雨量在平地上的积水厚度(mm)进行如下定义:如图 2-9-1 所示,小明用一个底面直径为 200 mm,高为 300 mm 的圆锥形容器接了 24 小时的雨水,积水深度为150 mm,那么这 24 小时降雨的等级是(平地降雨量等于圆
锥形容器内积水的体积除以容器口面积)(
A.小雨C.大雨答案:B
考点一 用函数图象刻画变化过程1.(2020 年新高考Ⅱ改编)我国新冠肺炎疫情防控进入常态化,各地有序推动复工复产,图 2-9-2 是某地连续 11
天复工复产指数折线图,下列说法正确的是(图 2-9-2
①这 11 天复工指数和复产指数均逐日增加;②这 11 天期间,复产指数的增量大于复工指数的增量;③第 3 天至第 11 天复工、复产指数均超过 80%;④第 9 天至第 11 天复产指数的增量大于复工指数的增量.
解析:由折线图知这 11 天的复工、复产指数有增有减,①错误;由第 1 天和第 11 天复工和复产指数位置可知,复产指数的增量小于复工指数的增量,②错误;由折线图知,第 3 天至第 11 天复工、复产指数均超过 80%,③正确;由折线图知,第 9 天至第 11 天复产指数增量大于复工指数的增量,④正确.故选 C.
2.汽车的“燃油效率”是指汽车每消耗 1 升汽油行驶的里程,图 2-9-3 描述了甲、乙、丙三辆汽车在不同速度
下的燃油效率情况.下列叙述中正确的是(图 2-9-3
A.消耗 1 升汽油,乙车最多可行驶 5 千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽
C.甲车以 80 千米/时的速度行驶 1 小时,消耗 10 升
D.某城市机动车最高限速 80 千米/时,相同条件下,
在该市用丙车比用乙车更省油
解析:根据图象知消耗 1 升汽油,乙车最多行驶里程大于 5 千米,A 错误;以相同速度行驶时,甲车燃油效率最高,因此以相同速度行驶相同路程时,甲车消耗汽油最少,B 错误;甲车以 80 千米/时的速度行驶时燃油效率为10 千米/升,行驶 1 小时,里程为 80 千米,消耗 8 升汽油,C 错误;最高限速 80 千米/时,丙车的燃油效率比乙车高,因此相同条件下,在该市用丙车比用乙车更省油,D 正确.
3.如图 2-9-4,有一直角墙角,两边的长度足够长,若P 处有一棵树与两墙的距离分别是 4 m 和 a m(0<a<12).不考虑树的粗细,现用 16 m 长的篱笆,借助墙角围成一个矩形花圃 ABCD,设此矩形花圃的最大面积为 u,若将这棵树围在矩形花圃内,
则函数 u=f(a)(单位:m2)的图象大致是(
解析:设 AD 的长为 x m,则 CD 的长为(16-x) m,则矩形 ABCD 的面积为 x(16-x) m2.因为要将点 P 围在矩形 ABCD 内,所以 a≤x≤12.当 0<a≤8 时,当且仅当 x=8 时,u=64;当 8<a<12 时,u=a(16-a).作出函数图象可得其形状与 B 选项接近.故选 B.
【题后反思】判断函数图象与实际问题变化过程相吻
(1)构建函数模型法:根据题意易构建函数模型时,先
建立函数模型,再结合模型选择图象.
(2)验证法:根据实际问题中两变量的变化快慢等特点,结合图象的变化趋势,验证是否吻合,从中排除不符合实际的情况,选择出符合实际情况的答案.
考点二 构造函数模型求解实际问题考向 1 二次函数、分段函数模型[例 1]某企业生产 A,B 两种产品,根据市场调查与预测,A 产品的利润 y 与投资 x 成正比,其关系如图 2-9-5;B 产品的利润与投资的算术平方根成正比,其关系如图2-9-6.(利润和投资单位:万元)
(1)分别将 A,B 两种产品的利润表示为投资的函数关
(2)已知该企业已筹集到 18 万元资金,并将全部投入
A,B 两种产品的生产.
①若平均投入生产两种产品,可获得多少利润?②如果你是厂长,怎样分配这 18 万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
此时 x=16,18-x=2.
∴当 A,B 两种产品分别投入 2 万元,16 万元时,可
使该企业获得最大利润,最大利润为 8.5 万元.
考向 2 构建指数(对数)型函数模型[例 2]一片森林原来面积为 a,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是 10 年,为保护生态环境,森林面积至少要保留
(1)求每年砍伐面积的百分比;(2)到今年为止,该森林已砍伐了多少年?
解:(1)设每年砍伐面积的百分比为 x(0
解析:根据图象求得 y=-(x-6)2+11(x>0),
∴要使年平均利润最大,客车营运年数为 5.
(1)指数函数、对数函数模型解题,关键是对模型的判断,先设定模型,将有关数据代入验证,确定参数,求解时要准确进行指数、对数运算,灵活进行指数与对数的互化.
(2)实际问题中有些变量间的关系不能用同一个关系式给出,而是由几个不同的关系式构成,如出租车计价与路程之间的关系,应构建分段函数模型求解.但应关注以下两点:
①分段要简洁合理,不重不漏;②分段函数的最值是
各段的最大(或最小)值中的最大(或最小)值.
【考法全练】1.(考向 1)(2021 年新乡期中)2021 年 9 月 10 日,小王开始读小学一年级,小王父母决定给他开一张银行卡,每月的 16 号存钱至该银行卡(假设当天存钱当天到账).用于小王今后的教育开支.2021 年 9 月 16 日小王父母往卡上存入 500 元.以后每月存的钱数比上个月多 100 元,则他这张银行卡账上存钱总额(不含银行利息)首次达到 100 000 元
A.2024 年 11 月 16 日C.2025 年 1 月 16 日
B.2024 年 12 月 16 日D.2025 年 2 月 16 日
解析:由题可知,小王父母从 2021 年 9 月开始,每月所存钱数依次成首项为 500,公差为 100 的等差数列,
∴第 41 个月的 16 号存完钱后,他这张银行卡账上存钱总额(不含银行利息)首次达到 100 000 元,故 2025 年 1月 16 日他这张银行卡账上存钱总额(不含银行利息)首次达到 100 000 元.故选 C.
令50n2+450n≥100 000,即n2+9n≥2 000,∵402+9×40<2 000,412+9×41>2 000,
2.(考向 2)(2020 年新高考Ⅰ)基本再生数 R0 与世代间隔T 是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:I(t)=ert 描述累计感染病例数 I(t)随时间 t(单位:天)的变化规律,指数增长率 r 与 R0,T 近似满足 R0=1+rT.有学者基于已有数据估计出 R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加 1 倍需要的时间约为(ln 2
3.(考向 3)某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边夹角为 60°(如图 2-9-8),考虑防洪堤坚固
性及石块用料等因素,设计其横断面要求面积为 9
方米,且高度不低于 米.记防洪堤横断面的腰长为 x 米,外周长(梯形的上底线段 BC 与两腰长的和)为 y 米.要使防洪堤的上面与两侧面的水泥用料最省(即横断面的外周长最小),则防洪堤的腰长 x=________米.图 2-9-8
⊙已知函数模型求解实际问题[例 4]为了降低能源损耗,某体育馆的外墙需要建造隔热层,体育馆要建造可使用 20 年的隔热层,每厘米厚的隔热层建造成本为 6 万元. 该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度 x(单位:cm)满足关系:C(x)
消耗费用为 8 万元,设 f(x)为隔热层建造成本与 20 年的能源消耗费用之和.
(1)求 k 的值及 f(x)的表达式;
(2)隔热层修建多厚时,总费用 f(x)达到最小?并求最
此时 x=5,因此 f(x)的最小值为 70.∴隔热层修建 5 cm 厚时,总费用 f(x)达到最小,最小值为 70 万元.
【反思感悟】已知函数模型解决实际问题的关注点(1)认清所给函数模型,弄清哪些量为待定系数.
(2)根据已知利用待定系数法,确定模型中的待定系数.(3)利用该模型求解实际问题.
1.拟定甲、乙两地通话 m 分钟的电话费(单位:元)由f(m)=1.06(0.5[m]+1)给出,其中 m>0,[m]是不超过 m 的最大整数(如[3]=3,[3.7]=3,[3.1]=3),则甲、乙两地通话 6.5 分钟的电话费为________元.
解析:∵m=6.5,∴[m]=6,则 f(6.5)=1.06×(0.5×
2.(一题两空)某地西红柿上市后,通过市场调查,得到西红柿种植成本 Q(单位:元/100 kg)与上市时间 t(单位:天)的数据如下表:
根据上表数据,从下列函数中选取一个函数描述西红
柿种植成本 Q 与上市时间 t 的变化关系:
Q=at+b,Q=at2+bt+c,Q=a·bt,Q=a·lgbt.
利用你选取的函数,求:
①西红柿种植成本最低时的上市天数是________;②最低种植成本是________元/100 kg.
解析:因为随着时间的增加,种植成本先减少后增加,而且当 t=60 和 t=180 时种植成本相等,再结合题中给出的四种函数关系可知,种植成本与上市时间的变化关系应该用二次函数Q=at2+bt+c,即Q=a(t-120)2+m描述,将表中数据代入可得
新高考数学一轮复习课件第2章函数导数及其应用第8讲 函数与方程(含解析): 这是一份新高考数学一轮复习课件第2章函数导数及其应用第8讲 函数与方程(含解析),共44页。PPT课件主要包含了答案B,图2-8-3,答案12,图D12,图D13,答案3,个解就有几个零点,答案D,图2-8-4,答案1等内容,欢迎下载使用。
新高考数学一轮复习课件第2章函数导数及其应用第7讲 函数的图象(含解析): 这是一份新高考数学一轮复习课件第2章函数导数及其应用第7讲 函数的图象(含解析),共50页。PPT课件主要包含了描点法作图,2对称变换,3伸缩变换,4翻折变换,名师点睛,中心对称,的图象相同,答案A,答案C,题组三真题展现等内容,欢迎下载使用。
高考数学一轮总复习课件第2章函数导数及其应用第九讲函数模型及其应用(含解析): 这是一份高考数学一轮总复习课件第2章函数导数及其应用第九讲函数模型及其应用(含解析),共47页。PPT课件主要包含了答案ABCD,答案D,答案C,A①③,B②③④,C③④,D①④,答案B,合的两种方法,答案5等内容,欢迎下载使用。












