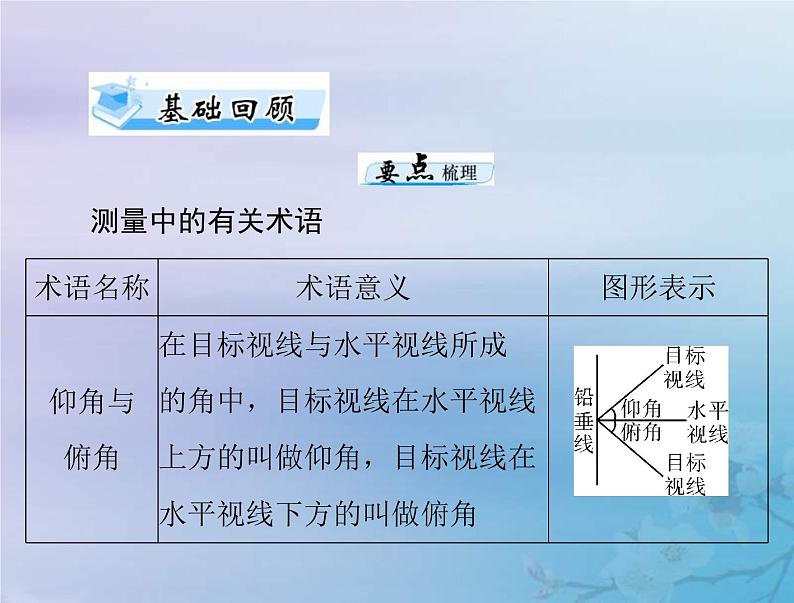
新高考数学一轮复习课件第3章三角函数解三角形第8讲 解三角形应用举例（含解析）

这是一份新高考数学一轮复习课件第3章三角函数解三角形第8讲 解三角形应用举例（含解析），共44页。PPT课件主要包含了测量中的有关术语，图3-8-1，答案A，题组三真题展现，图3-8-3，A346，B373，C446，D473，答案B等内容，欢迎下载使用。

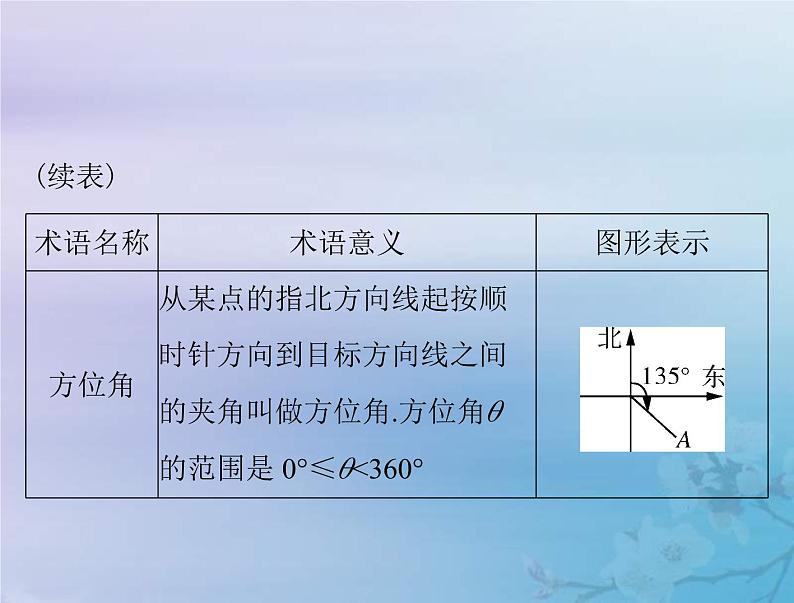
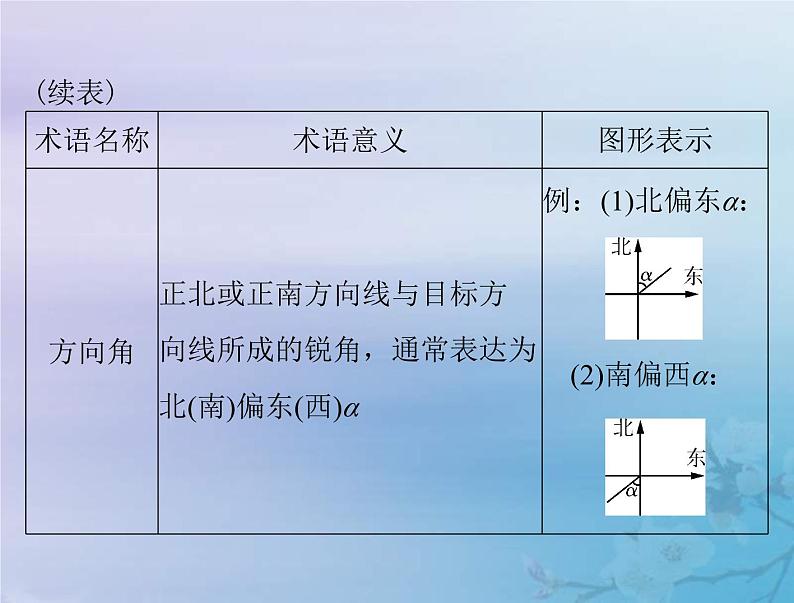
【名师点睛】易混淆方位角与方向角的概念
(1)方位角是指北方向线按顺时针旋转到目标方向线之间的水平夹角，而方向角是正北或正南方向线与目标方向线所成的锐角.
(2)“方位角”与“方向角”的范围：方位角大小的范
围是[0°，360°)，方向角大小的范围是[0°，90°).
题组一 走出误区1.判断下列结论正误(在括号内打“√”或“×”)
(1)东北方向就是北偏东 45°的方向.(
(2)从 A 处望 B 处的仰角为α，从 B 处望 A 处的俯角为
β，则α，β的关系为α＋β＝180°.(
(3)俯角是铅垂线与视线所成的角，其范围为
)(4)方位角与方向角其实质是一样的，均是确定观察点
与目标点之间的位置关系.(
答案：(1)√　 (2)× 　(3)×　 (4)√
题组二 走进教材2.(教材改编题)如图 3-8-1 所示，设 A，B 两点在河的两岸，一测量者在 A 点所在的同侧河岸边选定一点 C，测出 AC 的距离为50 m，∠ACB＝45°，∠CAB＝105°后，就
可以计算出 A，B 两点的距离为(　　)
3.(教材改编题)如图 3-8-2 所示，D，C，B 三点在地面的同一条直线上，DC＝a，从 C，D 两点测得 A 点的仰角分别为 60°，30°，则 A 点离地面的高度 AB＝________.图 3-8-2
4.(2021 年全国甲)2020 年 12 月 8 日，中国和尼泊尔联合公布珠穆朗玛峰最新高程为 8 848.86(单位：m)，三角高程测量法是珠峰高程测量方法之一.图 3-8-3 是三角高程测量法的一个示意图，现有 A，B，C 三点，且 A，B，C 在同一水平面上的投影A′，B′，C′满足∠A′C′B′＝45°，∠A′B′C′＝60°.由C点测得B点的仰角为15°，BB′与CC′的差为100；由B点测得A点的仰角为45°，
5.(2021 年全国乙)魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作，其中第一题是测量海岛的高.如图3-8-4，点 E，H，G 在水平线 AC 上，DE 和 FG 是两个垂直于水平面且等高的测量标杆的高度，称为“表高”，EG称为“表距”，GC 和 EH 都称为“表目距”，GC 与 EH
的差称为“表目距的差”，则海岛的高 AB＝(图 3-8-4
[例 1](2021 年宁德质检)海洋蓝洞是地球罕见的自然地理现象，被誉为“地球给人类保留宇宙秘密的最后遗产”，我国拥有世界上已知最深的海洋蓝洞.若要测量如图3-8-5 所示的海洋蓝洞的口径(即 A，B 两点间的距离)，现取两点 C，D，测得 CD＝80，∠ADB＝135°，∠BDC＝
∠DCA＝15°，∠ACB＝120°，则图中海洋蓝洞的口径为
【题后反思】求距离问题的两个注意事项
(1)选定或确定要创建的三角形，首先确定所求量所在的三角形，若其他量已知，则直接求解；若有未知量，则把未知量放在另一确定三角形中求解.
(2)确定用正弦定理还是余弦定理，如果都可用，就选
(2021 年聊城期末)第十届中国花卉博览会于 2021 年 5月 21 日至 7 月 2 日在上海崇明举办，主题是“花开中国梦”，其标志建筑世纪馆以“蝶恋花”为设计理念，利用国际前沿的数字技术，突破物理空间局限，打造了一个万花竞放的虚拟绚丽空间，拥有全国跨度最大的自由曲面混凝土壳体，屋顶跨度达 280 米.图 3-8-6 为世纪馆真实图，图 3-8-7 是世纪馆的简化图.世纪馆的简化图可近似看成是
解析：如图 D20 所示，过 B 点作 AA′的垂线，垂足为 H，图 D20
考点二 测量高度问题[例 2](2021 年运城期末)如图 3-8-8，一辆汽车在一条水平的公路上向正西方向行驶，到 A 处时测得公路北侧一山顶D在西偏北45°的方向上，行驶600 m后到达 B 处，测得此山顶在西偏北75°的方向上，仰角为 60°，则此山的高度CD
(1)在处理有关高度问题时，要理解仰角、俯角(它们是在铅垂面上所成的角)、方向(位)角(它们是在水平面上所成的角)是关键.
(2)在实际问题中，可能会遇到空间与平面(地面)同时研究的问题，这时最好画两个图形，一个空间图形，一个平面图形，这样处理起来既清楚又不容易搞错.
(3)注意山或塔垂直于地面或海平面，把空间问题转化
【变式训练】如图 3-8-9，测量河对岸的塔高 AB 时可以选与塔底 B在同一水平面内的两个测点 C 与 D，测得∠BCD＝15°，∠BDC＝30°，CD＝30，并在点 C 测得塔顶 A 的仰角为
60°，则塔高 AB 等于(　　)
考点三 测量角度问题[例3]如图 3-8-10，已知岛 A 南偏西 38°方向，距岛 A 3海里的 B 处有一艘缉私艇.岛 A 处的一艘走私船正以 10 海里/时的速度向岛 A 北偏西22°方向行驶，问缉私艇朝何方向以多大速度行驶，恰好用 0.5 小时能截住该走私船？
解：如图 3-8-11，设缉私艇在 C 处截住走私船，D 为岛 A 正南方向上一点，缉私艇的速度为每小时 x 海里，则BC＝0.5x，AC＝5，依题意得，∠BAC＝180°－38°－22°＝120°，
由余弦定理可得BC2＝AB2＋AC2－2AB·ACcs 120°，所以 BC2＝49，所以 BC＝0.5x＝7，解得 x＝14.
又∠BAD＝38°，所以 BC∥AD，故缉私艇以每小时 14 海里的速度向正北方向行驶，恰好用 0.5 小时截住该走私船.
(1)测量角度问题的关键是在弄清题意的基础上，画出表示实际问题的图形，并在图形中标出有关的角和距离，再用正弦定理或余弦定理解三角形，最后将解得的结果转化为实际问题的解.
(2)方向角是相对于某点而言的，因此在确定方向角
时，必须先弄清楚是哪一个点的方向角.
【变式训练】如图 3-8-12，两座相距 60 m 的建筑物 AB，CD 的高度分别为 20 m,50 m，BD 为水平面，则从建筑物 AB 的顶端
A 看建筑物 CD 的张角∠CAD 等于(图 3-8-12
⊙解三角形中的综合问题
(1)解三角形中的综合问题，除灵活运用正、余弦定理及三角形的有关知识外，一般还要用到三角函数，三角恒等变换，平面向量等知识，因此掌握正、余弦定理，三角函数的公式及性质是解题关键.
(2)三角形问题中，涉及变量取值范围或最值问题要注
2.四边形 ABCD 的内角 A 与 C 互补，AB＝1，BC＝3，
(1)求角 C 和 BD；
(2)求四边形 ABCD 的面积.