






新高考数学一轮复习课件第6章立体几何第3讲 点直线平面之间的位置关系(含解析)
展开基本事实 1:过不在一条直线上的三个点,有且只有
基本事实 2:如果一条直线上的两个点在一个平面内,
那么这条直线在此平面内.
基本事实 3:如果两个不重合的平面有一个公共点,
那么它们有且只有一条过该点的公共直线.
基本事实 4:平行于同一条直线的两条直线平行.
2.直线与直线的位置关系(1)位置关系的分类
(2)异面直线所成的角①定义:设 a,b 是两条异面直线,经过空间任一点 O作直线a′∥a,b′∥b,把a′与b′所成的锐角(或直角)叫做异面直线 a 与 b 所成的角(或夹角).
3.直线与平面的位置关系有直线在平面内、直线与平
面相交、直线与平面平行三种情况.
4.平面与平面的位置关系有平行、相交两种情况.5.等角定理
空间中如果两个角的两边分别对应平行,那么这两个
题组一 走出误区1.(多选题)设α是给定的平面,A,B 是不在α内的任意
两点,则下列说法一定正确的是(A.在α内存在直线与直线 AB 异面B.在α内存在直线与直线 AB 相交C.在α内存在直线与直线 AB 平行D.存在过直线 AB 的平面与α垂直答案:AD
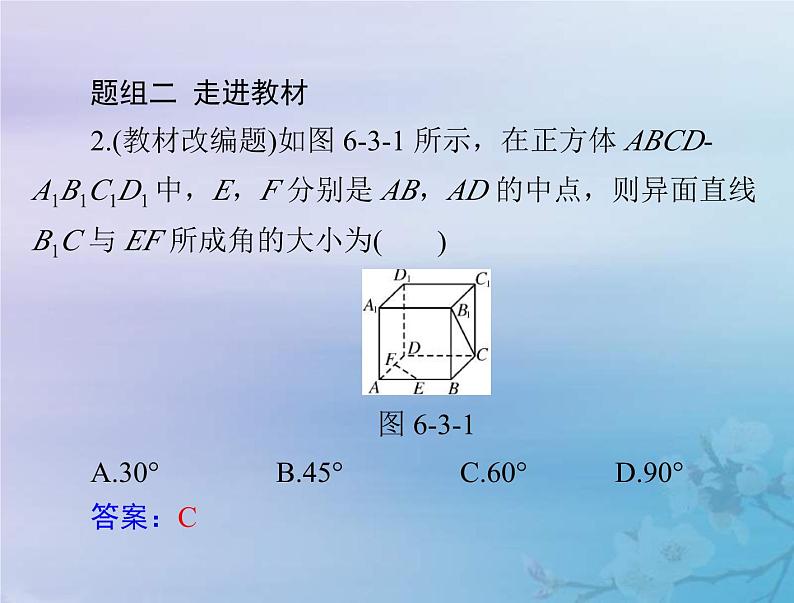
题组二 走进教材2.(教材改编题)如图 6-3-1 所示,在正方体 ABCD-A1B1C1D1 中,E,F 分别是 AB,AD 的中点,则异面直线
B1C 与 EF 所成角的大小为(
3.(教材改编题)用一个平面去截正方体,截面的形状不
B.正方形D.正六边形
A.正三角形C.正五边形答案:C
题组三 真题展现4.(2019 年全国Ⅲ)如图 6-3-2,点 N 为正方形 ABCD 的中心,△ECD 为正三角形,平面 ECD⊥平面 ABCD,M 是
线段 ED 的中点,则(
A.BM=EN,且直线 BM,EN 是相交直线B.BM≠EN,且直线 BM,EN 是相交直线C.BM=EN,且直线 BM,EN 是异面直线D.BM≠EN,且直线 BM,EN 是异面直线答案:B
5.(2019 年上海)已知平面α,β,γ两两垂直,直线 a,b,c 满足:a⊆α,b⊆β,c⊆γ,则直线 a,b,c 不可能满足以
B.两两平行D.两两异面
下哪种关系(A.两两垂直C.两两相交答案:B
考点一 平面的基本性质1.(2021 年枣庄期末)有结论:①不共线的三点确定一个平面;②平行于同一条直线的两条直线平行;③经过两条平行直线,有且只有一个平面.
其中公理(基本事实)的个数是(
解析:基本事实 1:过不在一条直线上的三个点,有
且只有一个平面,①是基本事实,
基本事实 4:平行于同一条直线的两条直线平行,②
经过两条平行直线,有且只有一个平面,为共面的判
定定理,③不是基本事实,
故基本事实的个数为 2 个.故选 C.
2.在三棱锥 A-BCD 的边 AB,BC,CD,DA 上分别取
E,F,G,H 四点.如果 EF∩HG=P,则点 P(A.一定在直线 BD 上B.一定在直线 AC 上C.在直线 AC 或 BD 上D.不在直线 AC 上,也不在直线 BD 上
解析:如图 D38 所示,因为 EF⊂平面 ABC,HG⊂平面 ACD,EF∩HG=P,所以 P∈平面 ABC,P∈平面 ACD.又因为平面 ABC∩平面 ACD=AC,所以 P∈AC.故选 B.
3.(多选题)(2020 年全国Ⅱ改编)下列选项正确的是
)A.两两相交且不过同一点的三条直线必在同一平面内B.过空间中任意三点有且仅有一个平面C.若空间两条直线不相交,则这两条直线平行D.若直线 l⊂平面α,直线 m⊥平面α,则 m⊥l
解析:对于 A,可设 l1 与 l2 相交,这两条直线确定的平面为α;若 l3 与 l1 相交,则交点 B 在平面α内,同理,l3与 l2 的交点 A 也在平面α内,所以,AB⊂α,即 l3⊂α,A正确;对于 B,若三点共线,则过这三个点的平面有无数个,B 错误;对于 C,空间中两条直线可能相交、平行或异面,C 错误;对于 D,若直线 m⊥平面α,则 m 垂直于平面α内所有直线.因为直线 l⊂平面α,所以直线 m⊥直线 l,D 正确.故选 AD.
【题后反思】共面、共线、共点问题的证明
(1)证明共面的方法:一是先确定一个平面,然后再证其余的线(或点)在这个平面内;二是证明两平面重合.(2)证明共线的方法:一是先由两点确定一条直线,再证其他各点都在这条直线上;二是直接证明这些点都在同一条特定直线上.
(3)证明线共点问题的常用方法:先证其中两条直线交
于一点,再证其他直线经过该点.
考点二 判断空间两直线的位置关系[例1](1)α是一个平面,m,n 是两条直线,A 是一个点,
α,n⊂α,且 A∈m,A∈α,则 m,n 的位置关系不
解析:依题意,m∩α=A,n⊂α,∴m 与 n 可能异面、相交(垂直是相交的特例),一定不平行.答案:D
(2)(2021 年黄山期中)如图 6-3-3,已知平面α,β,且α∩β=l.在梯形 ABCD 中,AD∥BC,且 AB⊂α,CD⊂β.则下列
A.直线 AB 与 CD 可能为异面直线B.直线 AB,CD,l 相交于一点C.AB=CD
D.直线 AC 与 BD 可能为异面直线
解析:梯形 ABCD 中,AD∥BC,所以 AB,CD 是梯
形 ABCD 的两腰,
所以 AB,CD 是共面直线,A 错误;
由题意知,AB 与 CD 不一定相等,C 错误;
在梯形 ABCD 中,对角线 AC,BD 是共面直线,D 错
画出图形,如图 6-3-4 所示:
设 AB∩CD=M.又 AB⊂α,CD⊂β,所以 M∈α,
且 M∈β,所以 M∈α∩β.
又α∩β=l,所以 M∈l,即直线 AB,CD,l 相交于一
空间中两直线位置关系的判定,主要是异面、平行和垂直的判定.异面直线的判定可采用直接法或反证法;平行直线的判定可利用三角形(梯形)中位线的性质、基本事实 4及线面平行与面面平行的性质定理;垂直关系的判定往往利用线面垂直或面面垂直的性质来解决.
【变式训练】1.若直线 l1 和 l2 是异面直线,l1 在平面α内,l2 在平面β
内,l 是平面α与平面β的交线,则下列命题正确的是(A.l 与 l1,l2 都不相交B.l 与 l1,l2 都相交C.l 至多与 l1,l2 中的一条相交D.l 至少与 l1,l2 中的一条相交
解析:由直线 l1 和 l2 是异面直线可知 l1 与 l2 不平行,
故 l1,l2 中至少有一条与 l 相交.故选 D.
2.如图 6-3-5 所示,正方体 ABCD-A1B1C1D1 中,M,N分别为棱 C1D1,C1C 的中点,有以下四个结论:
①直线 AM 与 CC1 是相交直线;②直线 AM 与 BN 是平行直线;③直线 BN 与 MB1 是异面直线;④直线 AM 与 DD1 是异面直线.其中正确的结论为________.
解析:因为点 A 在平面 CDD1C1 外,点 M 在平面
CDD1C1内,直线CC1在平面CDD1C1内,CC1不过点M,所以AM与CC1是异面直线,①错误;取DD1中点E,连接AE(图略),则BN∥AE,但AE与AM相交,②错误;因为B1与BN都在平面BCC1B1内,M在平面BCC1B1外,BN不过点B1,所以BN与MB1是异面直线,③正确;同理④正确.填③④.
考点三 求两条异面直线所成的角[例 2](2021 年青岛模拟)如图 6-3-6,在底面为正方形,侧棱垂直于底面的四棱柱 ABCD-A1B1C1D1 中,AA1 =2AB
=2,则异面直线 A1B 与 AD1 所成角的余弦值为(图 6-3-6
【题后反思】用平移法求异面直线所成的角的三个
(1)一作:根据定义作平行线,作出异面直线所成的角.(2)二证:证明作出的角是异面直线所成的角.(3)三求:解三角形,求出所作的角.
【变式训练】1.(2021 年聊城一模)如图 6-3-8,圆柱的轴截面 ABCD为正方形,E 为弧 BC 的中点,则异面直线 AE 与 BC 所成
解析:如图 D39,过点 E 作圆柱的母线交下底面于点
F,连接 AF,易知 F 为 的中点,
⊙构造模型解决空间线、面位置关系[例 3]已知 m,n 是两条不同的直线,α,β为两个不同的平面,有下列四个命题:①若 m⊥α,n⊥α,则 m∥n;②若 m∥α,n∥α,则 m∥n;③若 n∥α,m∥β,α∥β,则 m∥n;④若 m⊥α,n∥β,α∥β,则 m⊥n.
则以上命题中真命题的个数为(
解析:垂直于同一平面的两条直线平行,即①为真命
若 m∥α,n∥α,则 m 与 n 的位置关系是平行、相交
或异面,即②为假命题;
若 n∥α,m∥β,α∥β,则 m 与 n 的位置关系是平行、
相交或异面,即③为假命题;
因为 m⊥α,α∥β,所以 m⊥β,又 n∥β,所以 m⊥n,
(1)构造法实质上是结合题意构造适合题意的直观模型,然后将问题利用模型直观地作出判断,这样减少了抽象性,避免了因考虑不全面而导致解题错误.
(2)由于长方体或正方体中包含了线线平行、线面平行、面面平行、线线垂直、线面垂直及面面垂直等各种位置关系,故构造长方体或正方体来判断空间直线、平面间的位置关系,显得直观、易判断.构造时注意其灵活性,想象各种情况反复验证.
【高分训练】1.(2021 年郑州模拟)已知空间三条直线 l,m,n,若 l
与 m 垂直,l 与 n 垂直,则(
A.m 与 n 异面B.m 与 n 相交C.m 与 n 平行D.m 与 n 平行、相交、异面均有可能
解析:空间三条直线 l,m,n,当 l 与 m 垂直,且 l与 n 垂直时,m 与 n 可能平行,也可能相交,也可能异面.故选 D.
2.已知 m,n,l 为不同的直线,α,β为不同的平面,
则下列四个命题正确的是(
A.m,n 为异面直线,m∥α,n∥α,且 l⊥m,l⊥n,则 l⊥αB.若 m∥α,且 n⊥m,则有 n⊥αC.若α⊥β,m∥n,n⊥β,则 m∥αD.m 与α相交但不垂直,则与直线 m 平行的平面不可能与平面α垂直
2025版高考数学一轮总复习第7章立体几何第2讲空间点直线平面之间的位置关系课件: 这是一份2025版高考数学一轮总复习第7章立体几何第2讲空间点直线平面之间的位置关系课件,共60页。PPT课件主要包含了不共线,两个点,只有一条过该点,这条直线外一点,锐角或直角,相等或互补,AC=BD,ABC,ACD,向量法等内容,欢迎下载使用。
高考数学一轮总复习课件第6章立体几何第3讲点直线平面之间的位置关系(含解析): 这是一份高考数学一轮总复习课件第6章立体几何第3讲点直线平面之间的位置关系(含解析),共45页。PPT课件主要包含了A30°,B45°,C60°,D90°,答案C,是基本事实,图D38,答案B,答案AD,图6-3-4等内容,欢迎下载使用。
备战2024年高考总复习一轮(数学)第8章 立体几何 第3节 空间点、直线、平面之间的位置关系课件PPT: 这是一份备战2024年高考总复习一轮(数学)第8章 立体几何 第3节 空间点、直线、平面之间的位置关系课件PPT,共32页。PPT课件主要包含了内容索引,强基础固本增分,研考点精准突破,平面的基本性质,同一条直线上的三点,有且只有一条,相等或互补,锐角或直角等内容,欢迎下载使用。












