






新高考数学一轮复习课件第9章计数原理概率随机变量及其分布第4讲 离散型随机变量及其分布列(含解析)
展开一般地,对于随机试验样本空间Ω中的每个样本点ω,都有唯一的实数 X(ω)与之对应,我们称 X 为随机变量.可能取值为有限个或可以一一列举的随机变量称为离散型随机变量.
2.离散型随机变量的分布列及性质
(1)一般地,若离散型随机变量 X 的可能取值为 x1 ,x2,…,xi,…,xn,X取每一个值xi(i=1,2,…,n)的概率P(X=xi)=pi,则表
称为离散型随机变量 X 的概率分布列,简称分布列.(2)离散型随机变量的分布列的性质:
①pi≥0(i=1,2,…,n);②p1+p2+…+pn=1.
3.离散型随机变量的分布列(1)两点分布列
这样的分布列叫做两点分布列或 0-1 分布列.
如果随机变量 X 的分布列为两点分布列,就称 X 服从
两点分布,而称 p=P(X=1)为成功概率.
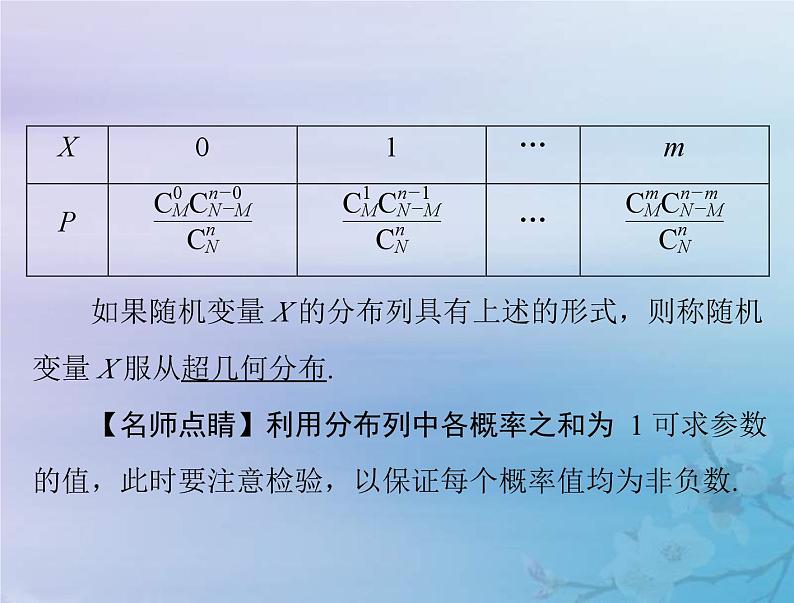
(2)超几何分布列一般地,假设一批产品共有 N 件,其中有 M 件次品.从 N 件产品中随机抽取 n 件(不放回),用 X 表示抽取的 n
如果随机变量 X 的分布列具有上述的形式,则称随机
变量 X 服从超几何分布.
【名师点睛】利用分布列中各概率之和为 1 可求参数的值,此时要注意检验,以保证每个概率值均为非负数.
1.判断下列结论正误(在括号内打“√”或“×”)(1)离散型随机变量的概率分布列中,各个概率之和可
(2)对于某个试验,离散型随机变量的取值可能有明确
的意义,也可能不具有实际意义.(
(3)如果随机变量 X 的分布列由下表给出,
(4)一个盒中装有 4 个黑球、3 个白球,从中任取一球,若是白球则取出来,若是黑球则放回盒中,直到把白球全部取出来,设取到黑球的次数为 X ,则 X 服从超几何分
2.(教材改编题)设随机变量 X 的分布列如下:
3.(教材改编题)有一批产品共 12 件,其中次品 3 件,每次从中任取一件,在取到合格品之前取出的次品数 X 的所有可能取值是__________.
离散型随机变量分布列的性质
1.随机变量 X 的分布列如下:其中 a,b,c 成等差数列,则 P(|X|=1)=________,公差 d 的取值范围是________.
3.设离散型随机变量 X 的分布列为
(1)求随机变量 Y=2X+1 的分布列;(2)求随机变量η=|X-1|的分布列;(3)求随机变量ξ=X2 的分布列.
解:(1)由分布列的性质知,0.2+0.1+0.1+0.3+m=1,
从而 Y=2X+1 的分布列为
∴P(η=0)=P(X=1)=0.1,
P(η=1)=P(X=0)+P(X=2)=0.2+0.1=0.3,P(η=2)=P(X=3)=0.3,P(η=3)=P(X=4)=0.3.故η=|X-1|的分布列为
从而ξ=X2的分布列为
【题后反思】分布列性质的两个作用
(1)利用分布列中各事件概率之和为 1 可求参数的值及
(2)随机变量 X 所取的值分别对应的事件是两两互斥的,利用这一点可以求随机变量在某个范围内的概率.
求离散型随机变量的分布列
[例 1]某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利 500 元.若供大于求,则每台多余的空调器需交保管费 100 元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润 200 元.(1)若该商场某周初购进 20 台空调器,求当周的利润(单位:元)关于当周需求量 n(单位:台,n∈N)的函数解析式 f(n);
(2)该商场记录了去年夏天(共 10 周)的空调器周需求
量 n(单位:台,n∈N),整理得下表.
以记录的每周需求量的频率作为每周需求量的概率,若商场某周初购进 20 台空调器,X 表示当周的利润(单位:元),求 X 的分布列.
解:(1)当 n≥20 且 n∈N 时,f(n)=500×20+200×(n-20)=200n+6 000,当 n≤19 且 n∈N 时,f(n)=500×n-100×(20-n)=600n-2 000,
(2)由(1)得 f(18)=8 800,f(19)=9 400,f(20)=10 000,
f(21)=10 200,f(22)=10 400,
所以当周的利润 X 的所有可能取值分别为 8 800 ,
9 400,10 000,10 200,10 400,
易知 P(X=8 800)=0.1,P(X=9 400)=0.2,P(X=10 000)=0.3,P(X=10 200)=0.3,P(X=10 400)=0.1.所以 X的分布列为
【题后反思】离散型随机变量分布列的求解步骤
为创建国家级文明城市,某城市号召出租车司机在高考期间至少进行一次“爱心送考”,该城市某出租车公司共 200 名司机,他们进行“爱心送考”的次数统计如图9-6-1 所示.
(1)求该出租车公司的司机进行“爱心送考”的人均次数;(2)从这 200 名司机中任选两人,设这两人进行送考次数之差的绝对值为随机变量 X,求 X 的分布列.解:(1)由统计图得 200 名司机中送考 1 次的有 20 人,送考 2 次的有 100 人,送考 3 次的有 80 人,∴该出租车公司的司机进行“爱心送考”的人均次数
(2)从该公司任选两名司机,记“这两人中一人送考 1次,另一人送考 2 次”为事件 A,“这两人中一人送考 2次,另一人送考 3 次”为事件 B,“这两人中一人送考 1次,另一人送考 3 次”为事件 C,“这两人送考次数相同”为事件 D,由题意知 X 的所有可能取值为 0,1,2,
[例 2]现要调查某县城居民对某项政策的知晓率,专家在进行评估时,从该县城的 10 个乡镇中随机抽取居民进行调查,知晓率为 90%及以上记为合格,否则记为不合格.已知该县城的 10 个乡镇中,有 7 个乡镇的居民的知晓率可达 90%,其余的均在 90%以下.(1)现从这 10 个乡镇中随机抽取 3 个进行调查,求抽到的乡镇中恰有 2 个乡镇不合格的概率;(2)若记从该县城随机抽取的 3 个乡镇中不合格的乡镇的个数为ξ,求ξ的分布列和数学期望.
【题后反思】超几何分布的实际应用问题,主要是指与两类不同元素的抽取问题的概率计算和离散型随机变量的分布列、期望及方差的求解等有关的问题.解题的关键如下:
①定型:根据已知建立相应的概率模型,并确定离散型随机变量服从的分布的类型,特别要区分超几何分布与二项分布.
②定参:确定超几何分布中的三个参数 N,M,n.即确定试验中包含的元素的个数、特殊元素的个数及要抽取的元素个数.
③列表:根据离散型随机变量的取值及其对应的概率
④求值:根据离散型随机变量的期望和方差公式,代
在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用.现有 6 名男志愿者 A1 ,A2 ,A3,A4,A5,A6 和 4 名女志愿者 B1,B2,B3,B4,从中随机抽取 5 人接受甲种心理暗示,另 5 人接受乙种心理暗示.
(1)求接受甲种心理暗示的志愿者中包含 A1 但不包含
(2)用 X 表示接受乙种心理暗示的女志愿者人数,求 X
⊙离散型随机变量分布列性质的交汇应用[例 3]设随机变量 X 的分布列如下:
答案:A【反思感悟】利用离散型随机变量分布列性质与等差中项交汇去求解,注意本题易忽视 a≥0,c≥0.
【高分训练】1.已知如表为离散型随机变量 X 的概率分布列,则概
率 P(X≥D(X))=(
2.若随机变量 X 的分布列为
则当 P(X
B.[1,2]D.(1,2)
新高考数学一轮复习课件第9章计数原理概率随机变量及其分布第5讲 条件概率二项分布与正态分布(含解析): 这是一份新高考数学一轮复习课件第9章计数原理概率随机变量及其分布第5讲 条件概率二项分布与正态分布(含解析),共60页。PPT课件主要包含了条件概率,事件的相互独立性,全概率公式,2二项分布,正态分布,图9-7-1,题组一,走出误区,答案1×,2×3√等内容,欢迎下载使用。
新高考数学一轮复习课件第9章计数原理概率随机变量及其分布第2讲 排列与组合(含解析): 这是一份新高考数学一轮复习课件第9章计数原理概率随机变量及其分布第2讲 排列与组合(含解析),共52页。PPT课件主要包含了排列与组合的概念,排列数与组合数,名师点睛,题组一,走出误区,答案1×,2×3×,题组二,走进教材,A60种等内容,欢迎下载使用。
新高考数学一轮复习课件第9章计数原理概率随机变量及其分布第1讲 分类加法计数原理与分步乘法计数原理(含解析): 这是一份新高考数学一轮复习课件第9章计数原理概率随机变量及其分布第1讲 分类加法计数原理与分步乘法计数原理(含解析),共37页。PPT课件主要包含了题组一,走出误区,以相同,接完成这件事,答案1×,2√3√,题组二,走进教材,答案24,题组三等内容,欢迎下载使用。












