新高考数学一轮复习讲与练第03讲 二次函数与一元二次方程、不等式（讲）（2份打包，原卷版+解析版）

这是一份新高考数学一轮复习讲与练第03讲 二次函数与一元二次方程、不等式（讲）（2份打包，原卷版+解析版），文件包含新高考数学一轮复习讲与练第03讲二次函数与一元二次方程不等式讲原卷版doc、新高考数学一轮复习讲与练第03讲二次函数与一元二次方程不等式讲解析版doc等2份试卷配套教学资源，其中试卷共11页， 欢迎下载使用。
本讲为基础知识点，题型主要和其他知识结合考察，属于运算类知识点，主要出现在最后的不等式运算中，结合二次函数图象深入了解函数图象在解不等式中的运用，从而解决更多的不等式运算问题。
考点一 二次函数解析式的三种形式
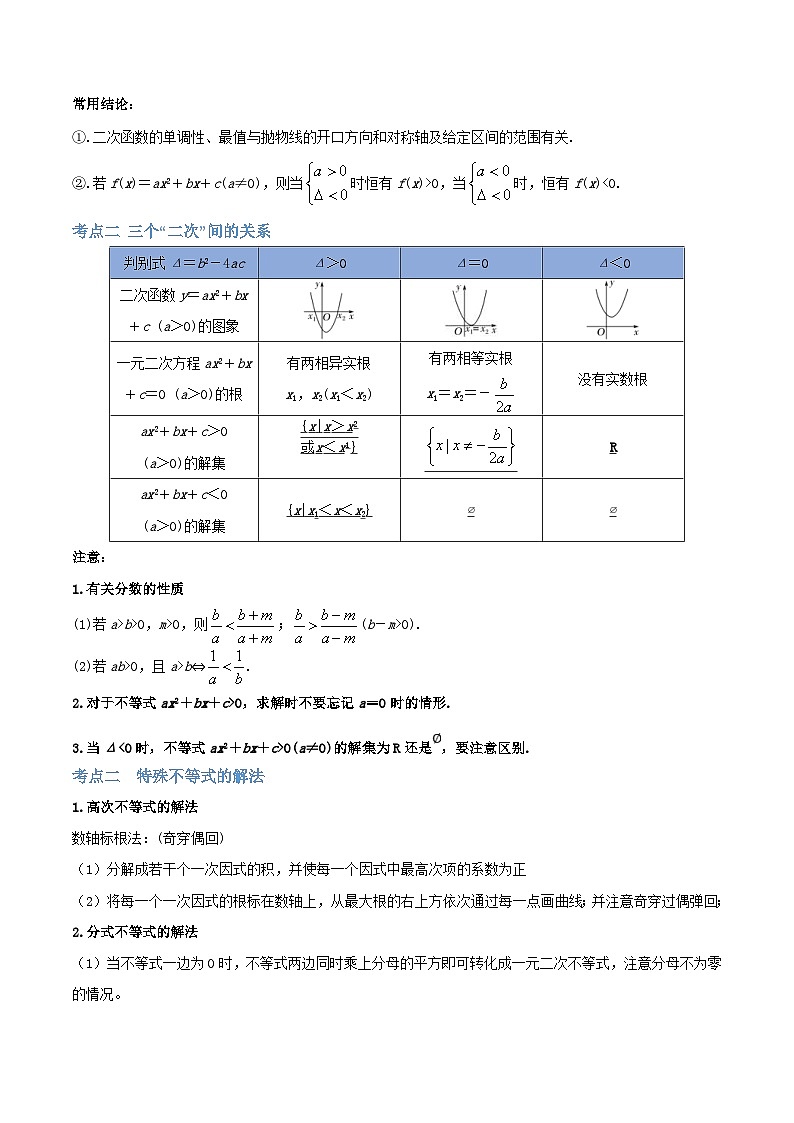
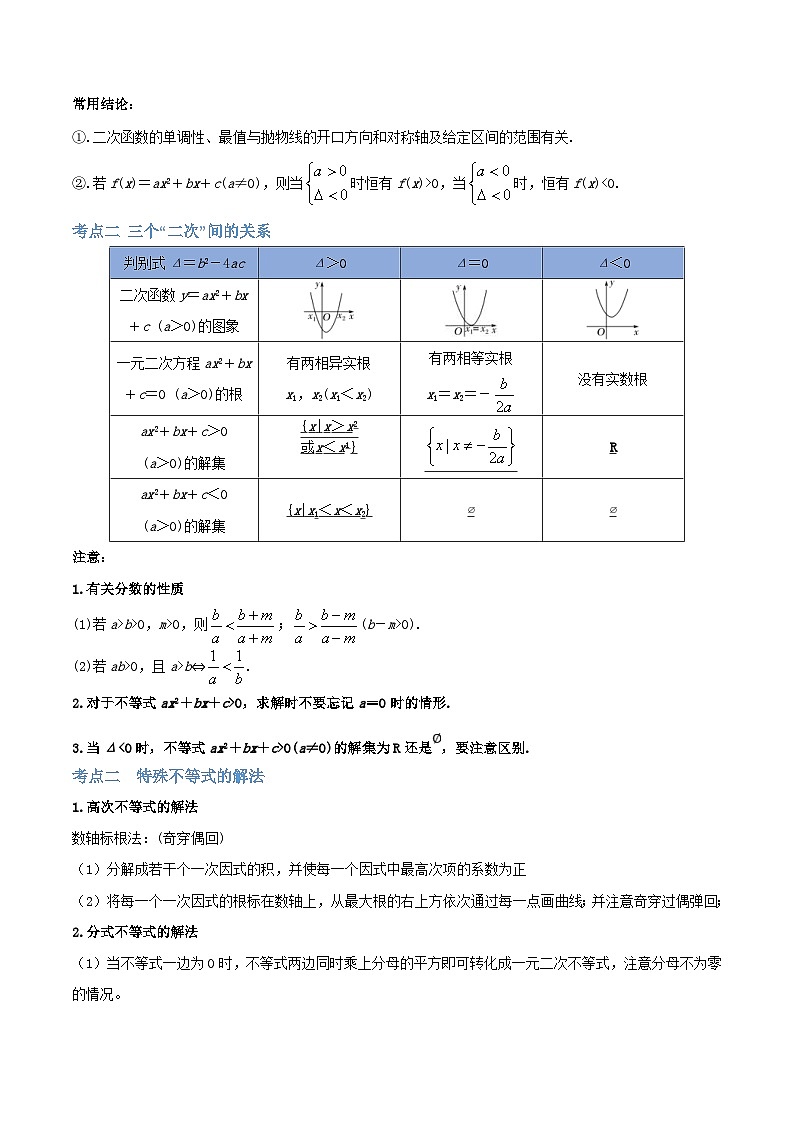
考点二 二次函数的图象与性质
常用结论：
①.二次函数的单调性、最值与抛物线的开口方向和对称轴及给定区间的范围有关.
②.若f(x)＝ax2＋bx＋c(a≠0)，则当 SKIPIF 1 < 0 时恒有f(x)>0，当 SKIPIF 1 < 0 时，恒有f(x)b>0，m>0，则 SKIPIF 1 < 0 ； SKIPIF 1 < 0 (b－m>0).
(2)若ab>0，且a>b⇔ SKIPIF 1 < 0 .
2.对于不等式ax2＋bx＋c>0，求解时不要忘记a＝0时的情形.
3.当Δ0(a≠0)的解集为R还是，要注意区别.
考点二 特殊不等式的解法
1.高次不等式的解法
数轴标根法：(奇穿偶回)
（1）分解成若干个一次因式的积，并使每一个因式中最高次项的系数为正
（2）将每一个一次因式的根标在数轴上，从最大根的右上方依次通过每一点画曲线；并注意奇穿过偶弹回；
2.分式不等式的解法
（1）当不等式一边为0时，不等式两边同时乘上分母的平方即可转化成一元二次不等式，注意分母不为零的情况。
（2）当不等式两边均不为零时需移至一边进行通分再进行转化运算。
高频考点一 二次函数与一元二次方程、不等式
例1、已知 SKIPIF 1 < 0 的解集为 SKIPIF 1 < 0 （ SKIPIF 1 < 0 ），则 SKIPIF 1 < 0 的值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C．1D．2
【变式训练】
1．已知方程 SKIPIF 1 < 0 的两根分别在区间 SKIPIF 1 < 0 ， SKIPIF 1 < 0 之内，则实数 SKIPIF 1 < 0 的取值范围为______．
高频考点二 高次不等式
例2、解不等式： SKIPIF 1 < 0
【变式训练】
1. 已知集合A={x|2 SKIPIF 1 < 0 |x| SKIPIF 1 < 0 m}，B={ SKIPIF 1 < 0 - SKIPIF 1 < 0 +8x>0}，C={ SKIPIF 1 < 0 -2x-15=0}.
(1)若A SKIPIF 1 < 0 C=A，求实数m的最小值;
(2)若 SKIPIF 1 < 0 ，求实数m的取值范围.
高频考点三 分式不等式
例3、 解关于 SKIPIF 1 < 0 的不等式 SKIPIF 1 < 0 ．
【变式训练】
1. 解关于 SKIPIF 1 < 0 的不等式 SKIPIF 1 < 0 ．
一般式
f(x)＝ax2＋bx＋c(a≠0)，图象的对称轴是x＝－ SKIPIF 1 < 0 ，顶点坐标是 SKIPIF 1 < 0
顶点式
f(x)＝a(x－m)2＋n(a≠0)，图象的对称轴是x＝m，顶点坐标是(m，n)
零点式
f(x)＝a(x－x1)(x－x2)(a≠0)，其中x1，x2是方程ax2＋bx＋c＝0的两根，图象的对称轴是x＝ SKIPIF 1 < 0
函数
y＝ax2＋bx＋c(a>0)
y＝ax2＋bx＋c(a