新高考数学一轮复习讲与练第24讲 抛物线（讲）（2份打包，原卷版+解析版）

这是一份新高考数学一轮复习讲与练第24讲 抛物线（讲）（2份打包，原卷版+解析版），文件包含新高考数学一轮复习讲与练第24讲抛物线讲原卷版doc、新高考数学一轮复习讲与练第24讲抛物线讲解析版doc等2份试卷配套教学资源，其中试卷共13页， 欢迎下载使用。

本讲为高考命题热点，分值22-27分，题型多变，选择题，填空题，解答题都会出现，
选择填空题常考圆锥曲线椭圆双曲线的离心率，几何关系等问题，大题题型多变，但多以最值，定值，范围，存在性问题，考察逻辑推理能力与运算求解能力.
考点一 抛物线的定义
平面内与一个定点F和一条定直线l(点F不在直线l上)的距离相等的点的轨迹叫做抛物线，定点F叫做抛物线的焦点，定直线l叫做抛物线的准线. eq \x(当定点在定直线上时，轨迹为过定点F与定直线l垂直的一条直线.)
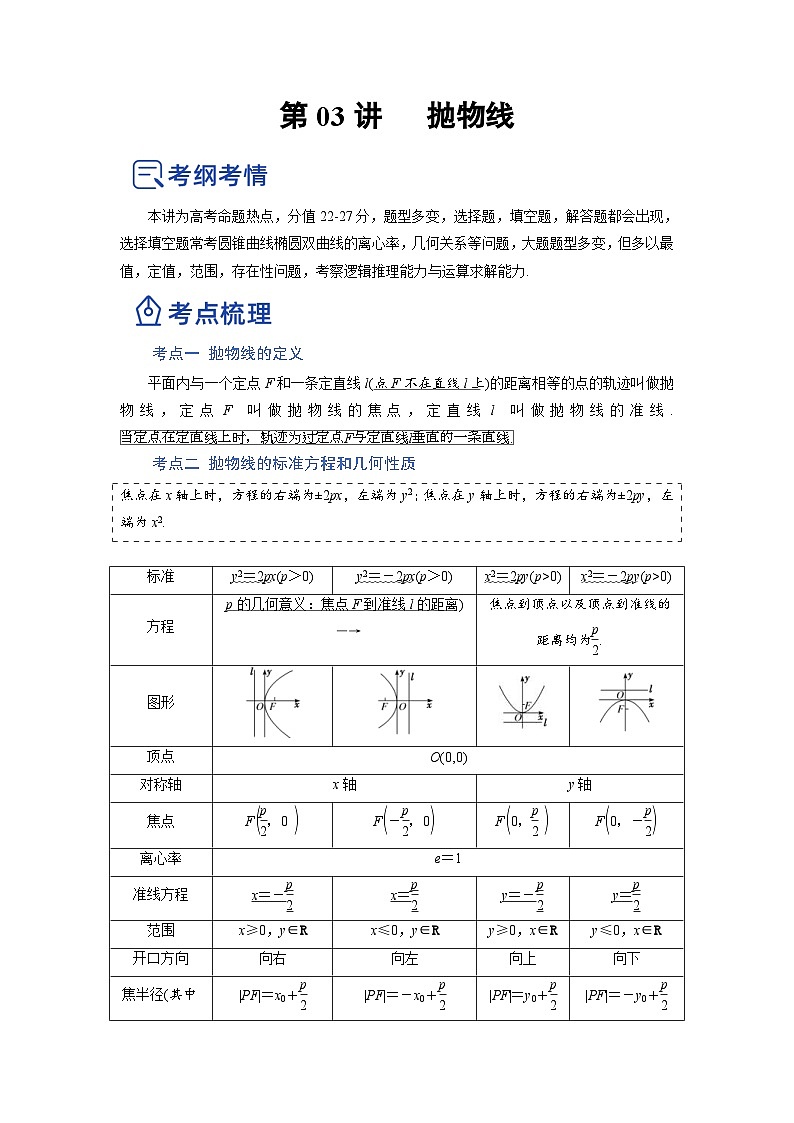
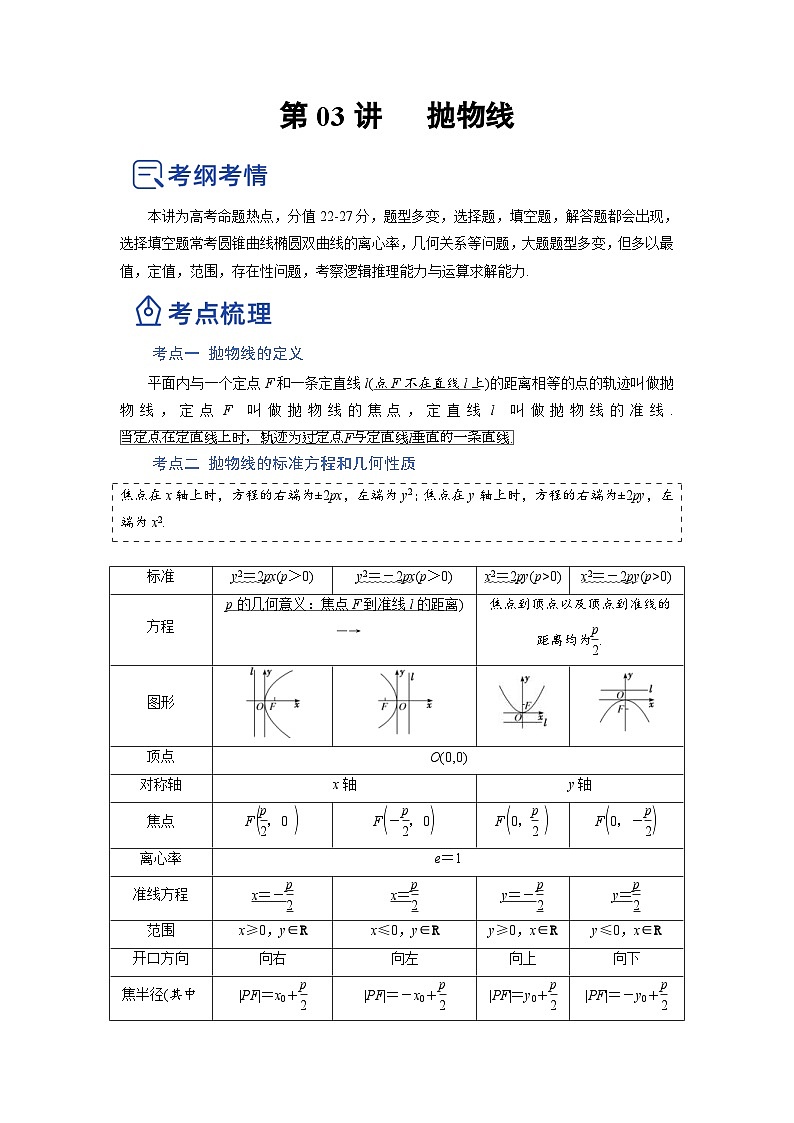
考点二 抛物线的标准方程和几何性质
焦点在x轴上时，方程的右端为±2px，左端为y2；焦点在y轴上时，方程的右端为±2py，左端为x2.
[常用结论]
与抛物线焦点弦有关的几个常用结论
设AB是过抛物线y2＝2px(p＞0)焦点F的弦，若A(x1，y1)，B(x2，y2)，α为弦AB的倾斜角．则
(1)x1x2＝eq \f(p2,4)，y1y2＝－p2.
(2)|AF|＝eq \f(p,1－cs α)，|BF|＝eq \f(p,1＋cs α).
(3)弦长|AB|＝x1＋x2＋p＝eq \f(2p,sin2α).
(4)eq \f(1,|AF|)＋eq \f(1,|BF|)＝eq \f(2,p).
(5)以弦AB为直径的圆与准线相切．
高频考点一 抛物线的定义及其应用
【例1】(1)若抛物线y2＝4x上一点P到其焦点F的距离为2，O为坐标原点，则△OFP的面积为( )
A.eq \f(1,2) B．1
C.eq \f(3,2) D．2
(2)设P是抛物线y2＝4x上的一个动点，若B(3,2)，则|PB|＋|PF|的最小值为________．
【方法技巧】
[解题技法]
与抛物线有关的最值问题，一般情况下都与抛物线的定义有关．“看到准线想焦点，看到焦点想准线”，这是解决与过抛物线焦点的弦有关问题的重要途径．
【跟踪训练】
1．若点A的坐标为(3,2)，F是抛物线y2＝2x的焦点，点M在抛物线上移动时，使|MF|＋|MA|取得最小值的M的坐标为________．
2．(2022·襄阳测试)已知抛物线y＝eq \f(1,2)x2的焦点为F，准线为l，M在l上，线段MF与抛物线交于N点，若|MN|＝eq \r(2)|NF|，则|MF|＝________.
高频考点二 抛物线的标准方程与几何性质
【例2】(1)(2019·全国卷Ⅱ)若抛物线y2＝2px(p>0)的焦点是椭圆eq \f(x2,3p)＋eq \f(y2,p)＝1的一个焦点，则p＝( )
A．2 B．3
C．4 D．8
(2)(2019·武汉调研)如图，过抛物线y2＝2px(p>0)的焦点F的直线l交抛物线于点A，B，交其准线于点C，若|BC|＝2|BF|，且|AF|＝6，则此抛物线方程为( )
A．y2＝9xB．y2＝6x
C．y2＝3xD．y2＝eq \r(3)x
【方法技巧】1．求抛物线标准方程的方法
(1)定义法：若题目已给出抛物线的方程(含有未知数p)，那么只需求出p即可．
(2)待定系数法：若题目未给出抛物线的方程，对于焦点在x轴上的抛物线的标准方程可统一设为y2＝ax(a≠0)，a的正负由题设来定；焦点在y轴上的抛物线的标准方程可设为x2＝ay(a≠0)，这样就减少了不必要的讨论．
2．抛物线性质的应用技巧
(1)利用抛物线方程确定及应用其焦点、准线时，关键是将抛物线方程化成标准方程．
(2)要结合图形分析，灵活运用平面图形的性质简化运算．
【变式训练】
1．(2020·福建厦门一模)若抛物线x2＝ay的焦点到准线的距离为1，则a＝( )
A．2 B．4
C．±2 D．±4
2．已知抛物线x2＝2py(p>0)的焦点为F，点P为抛物线上的动点，点M为其准线上的动点，若△FPM为边长是4的等边三角形，则此抛物线的方程为________．
高频考点三 直线与抛物线的位置关系
【例3】 (2019·全国卷Ⅰ)已知抛物线C：y2＝3x的焦点为F，斜率为eq \f(3,2)的直线l与C的交点为A，B，与x轴的交点为P.
(1)若|AF|＋|BF|＝4，求l的方程；
(2)若eq \(AP,\s\up7(―→))＝3eq \(PB,\s\up7(―→))，求|AB|.
[解] 设直线l：y＝eq \f(3,2)x＋t，A(x1，y1)，B(x2，y2)．
(1)由题设得Feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,4)，0))，故|AF|＋|BF|＝x1＋x2＋eq \f(3,2)，又|AF|＋|BF|＝4，所以x1＋x2＝eq \f(5,2).
由eq \b\lc\{\rc\ (\a\vs4\al\c1(y＝\f(3,2)x＋t，,y2＝3x))可得9x2＋12(t－1)x＋4t2＝0，
则x1＋x2＝－eq \f(12t－1,9).
从而－eq \f(12t－1,9)＝eq \f(5,2)，得t＝－eq \f(7,8).
所以l的方程为y＝eq \f(3,2)x－eq \f(7,8).
(2)由eq \(AP,\s\up7(―→))＝3eq \(PB,\s\up7(―→))可得y1＝－3y2.
由eq \b\lc\{\rc\ (\a\vs4\al\c1(y＝\f(3,2)x＋t，,y2＝3x))可得y2－2y＋2t＝0.
所以y1＋y2＝2.从而－3y2＋y2＝2，故y2＝－1，y1＝3.
代入C的方程得x1＝3，x2＝eq \f(1,3).故|AB|＝eq \f(4\r(13),3).
【方法技巧】
[解题技法]
1．直线与抛物线交点问题的解题思路
(1)求交点问题，通常解直线方程与抛物线方程组成的方程组．
(2)与交点相关的问题通常借助根与系数的关系或用向量法解决．
2．解决抛物线的弦及弦中点问题的常用方法
(1)有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用焦点弦公式，若不过焦点，则必须用一般弦长公式．
(2)涉及抛物线的弦长、中点、距离等相关问题时，一般利用根与系数的关系采用“设而不求”“整体代入”等解法．
[提醒] 涉及弦的中点、斜率时，一般用“点差法”求解．
【变式训练】
1．已知点M(－1,1)和抛物线C：y2＝4x，过C的焦点且斜率为k的直线与C交于A，B两点．若∠AMB＝90°，则k＝________.
2．设A，B为曲线C：y＝eq \f(x2,2)上两点，A与B的横坐标之和为2.
(1)求直线AB的斜率；
(2)设M为曲线C上一点，曲线C在点M处的切线与直线AB平行，且AM⊥BM，求直线AB的方程．
标准
y2＝2px(p＞0)
y2＝－2px(p＞0)
x2＝2py(p>0)
x2＝－2py(p>0)
方程
p的几何意义：焦点F到准线l的距离) eq \a\vs4\al(―→)
焦点到顶点以及顶点到准线的距离均为eq \a\vs4\al(\f(p,2).)
图形
顶点
O(0,0)
对称轴
x轴
y轴
焦点
Feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2)，0))
Feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(p,2)，0))
Feq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(p,2)))
Feq \b\lc\(\rc\)(\a\vs4\al\c1(0，－\f(p,2)))
离心率
e＝1
准线方程
x＝－eq \f(p,2)
x＝eq \f(p,2)
y＝－eq \f(p,2)
y＝eq \f(p,2)
范围
x≥0，y∈R
x≤0，y∈R
y≥0，x∈R
y≤0，x∈R
开口方向
向右
向左
向上
向下
焦半径(其中P(x0，y0))
|PF|＝x0＋eq \f(p,2)
|PF|＝－x0＋eq \f(p,2)
|PF|＝y0＋eq \f(p,2)
|PF|＝－y0＋eq \f(p,2)