



福建省厦门第一中学2023-2024学年高一上学期入学考试数学试题
展开数学试卷
本试卷共4页,满分150分
注意事项:
1.答题前,考生务必在试题卷、答题卡规定的地方填写自己的班级、座号、姓名.考生要认真核对答题卡上粘贴的条形码的“考号、姓名”与考生本人考号、姓名是否 一致.
2.回答选择题时,选出答案后用铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后再选涂其它答案标号.回答非选择题时,将答案写在答题卡上,写在本卷上无效.
3.考试结束,考生只须将答题卡交回.
一、单项选择题:本大题10小题,每小题5分,共50分.每小题只有一个正确答案.
1. PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,含有大量有毒、有害物质,也称可入肺颗粒物.将0.0000025用科学记数法表示为( )
A. B. C. D.
2. 已知,则下列关系一定正确的是( )
A.
B.
C.
D.
3. 一辆汽车开往距出发地420km目的地,若这辆汽车比原计划每小时多行10km,则提前1小时到达目的地.设这辆汽车原计划的速度是,根据题意所列方程是( )
A. B.
C. D.
4. 今年是我国现行宪法公布施行40周年.为贯彻党的二十大精神,强化宪法意识,弘扬宪法精神,推动宪法实施,某学校开展法律知识竞赛活动,全校一共100名学生参与其中,得分情况如下表.则分数的中位数和众数分别是( )
A. 80,90B. 90,100
C. 85,90D. 90,90
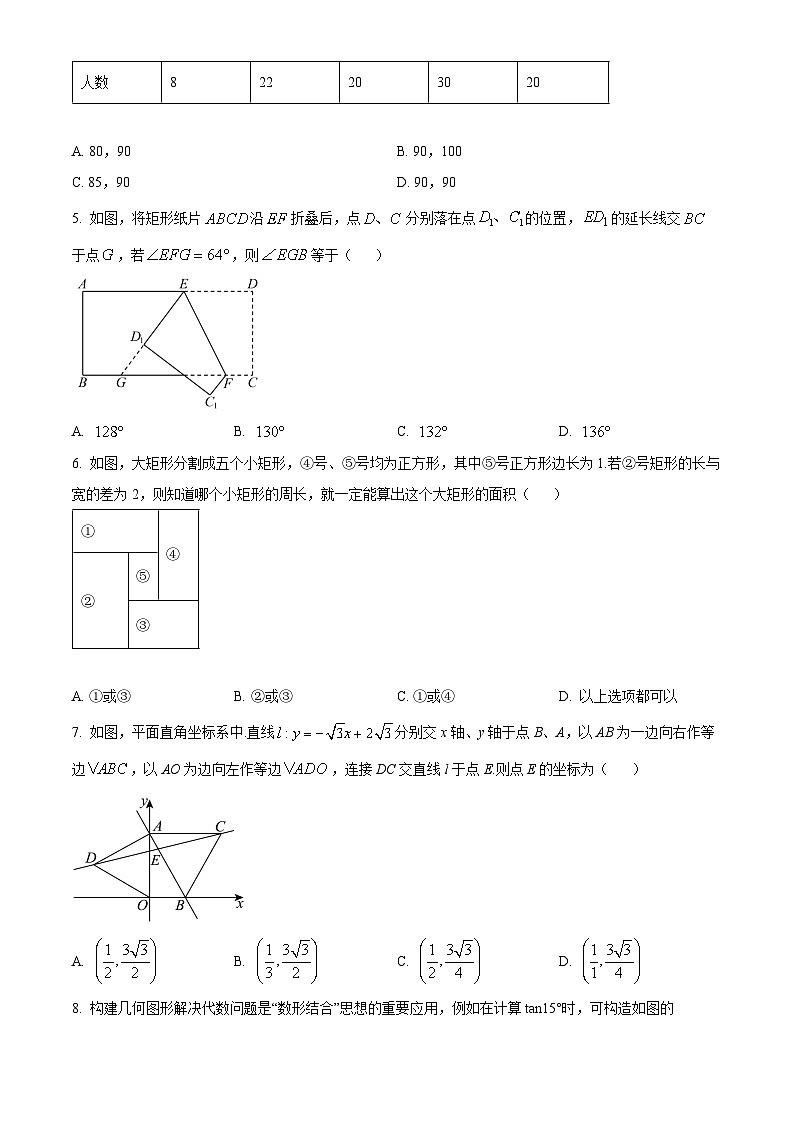
5. 如图,将矩形纸片沿折叠后,点分别落在点的位置,的延长线交于点,若,则等于( )
A. B. C. D.
6. 如图,大矩形分割成五个小矩形,④号、⑤号均为正方形,其中⑤号正方形边长为1.若②号矩形的长与宽的差为2,则知道哪个小矩形的周长,就一定能算出这个大矩形的面积( )
A. ①或③B. ②或③C. ①或④D. 以上选项都可以
7. 如图,平面直角坐标系中.直线分别交x轴、y轴于点B、A,以AB为一边向右作等边,以AO为边向左作等边,连接DC交直线l于点E.则点E的坐标为( )
A. B. C. D.
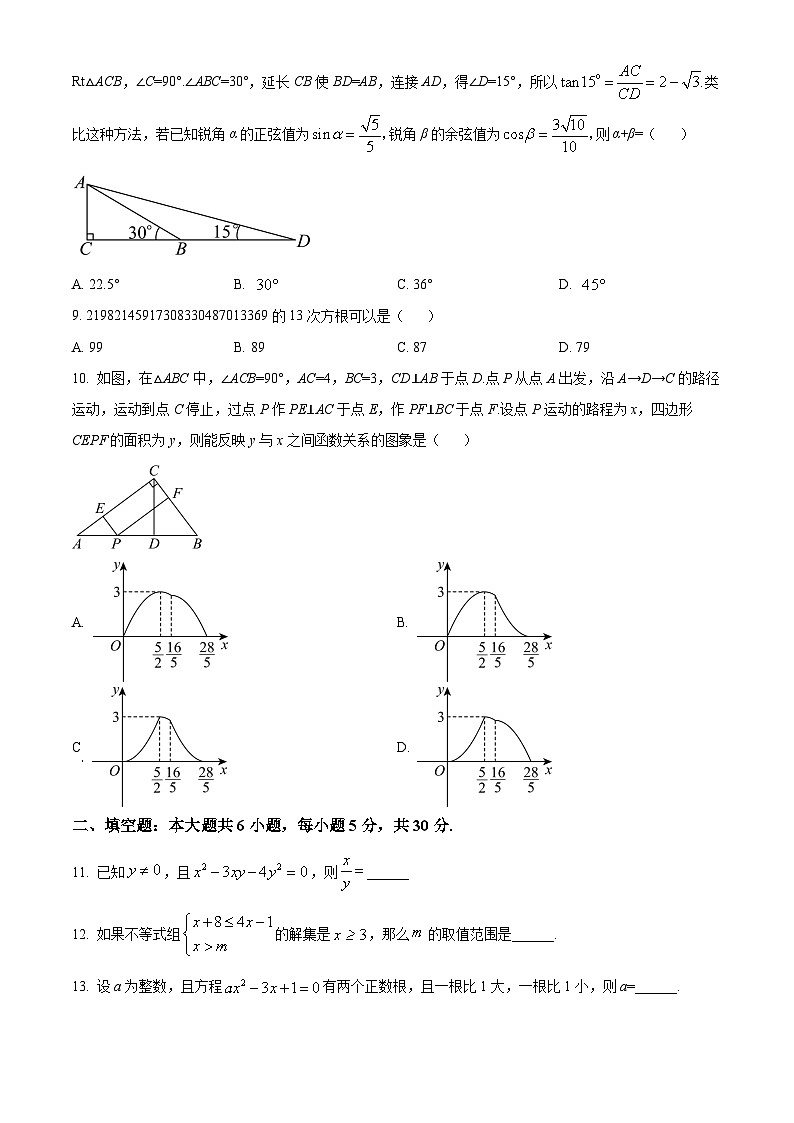
8. 构建几何图形解决代数问题是“数形结合”思想的重要应用,例如在计算tan15°时,可构造如图的Rt△ACB,∠C=90°.∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以类比这种方法,若已知锐角α的正弦值为锐角β的余弦值为则α+β=( )
A. 22.5°B. C. 36°D.
9. 21982145917308330487013369的13次方根可以是( )
A. 99B. 89C. 87D. 79
10. 如图,在△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB于点D.点P从点A出发,沿A→D→C的路径运动,运动到点C停止,过点P作PE⊥AC于点E,作PF⊥BC于点F.设点P运动的路程为x,四边形CEPF的面积为y,则能反映y与x之间函数关系的图象是( )
A. B.
C D.
二、填空题:本大题共6小题,每小题5分,共30分.
11. 已知,且,则______
12. 如果不等式组的解集是,那么的取值范围是______.
13. 设a为整数,且方程有两个正数根,且一根比1大,一根比1小,则a=______.
14. 在折纸手工中,我们时常需要对一张方形纸的某条边进行若干等分,若被要求折成两份,则很容易做到:但对于其他等分,例如五等分,则可以使用藤本近似折法进行操作,具体步骤如下:
(1)如图(1),在纸张大致的位置折出痕迹,用E表示与五等分位置的误差;
(2)如图(2),将折痕右边的部分对折;
(3)如图(3),将第(2)步折出的折痕右侧的部分对折;
(4)如图(4),将第(3)步折出的折痕左侧的部分对折;
(5)如图(5),将第(4)步折出的折痕左侧的部分对折.
最后的折痕将更加接近真实的五等分点位置,上述步骤具有可循环操作的特点,再次操作将会使得折痕更加精确.现已知小明有一条长度为70厘米的纸带,想要类比上述近似方法确定纸带上最左侧的七等分点,他在第一步折叠时,选取的折叠位置距离左边12厘米.若要使得最终确定的位置与实际位置误差小于0.5毫米,则最少需要进行______次折叠.(注:近似操作中每个步骤算作一次折叠).
15. 如图,直线y=3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y=(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=(k≠0)上的点D1处,则a=_____.
16. 已知中,点,,.则面积为________.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤,把解答过程填写在答题卡的相应位置.
17. (1)计算:;
(2)先化简再求值:其中
18. 已知关于的一元二次方程:有两个实数根.
(1)求的取值范围;
(2)若满足,求的值.
19. 教育部在《大中小学劳动教育指导纲要(试行)》中明确要求:初中生每周课外生活和家庭生活中,劳动时间不少于小时.某走读制初级中学为了解学生劳动时间的情况,对学生进行了随机抽样调查,并将调查结果制成不完整的统计图表,如图:
平均每周劳动时间的频数统计表
请根据图表信息,回答下列问题.
(1)参加此次调查总人数是_______人,频数统计表中_______;
(2)在扇形统计图中,组所在扇形的圆心角度数是_______;
(3)该校准备开展以“劳动美”为主题的教育活动,要从报名的男女中随机挑选人在活动中分享劳动心得,请用树状图或列表法求恰好抽到一名男生和一名女生的概率.
20. 如图,斜坡AB长130米,坡度现计划在斜坡中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
(1)若修建斜坡BE的坡角为求平台DE的长;(结果保留根号)
(2)斜坡AB正前方一座建筑物QM上悬挂了一幅巨型广告MN,小明在D点测得广告顶部M的仰角为他沿坡面DA走到坡脚A处,然后向大楼方向继续行走10米来到P处,测得广告底部N的仰角为此时小明距大楼底端Q处30米.已知B、C、A、M、Q在同一平面内,C、A、P、Q在同一条直线上,求广告MN的长度.(参考数据:sin3)
21. 如图,AB是⊙O的直径,点C是圆上的一点,于点D,AD交⊙O于点F,连接AC,若AC平分∠DAB,过点F作FG⊥AB于点G,交AC于点H,延长AB,DC交于点E.
(1)求证:是⊙O的切线;
(2)求证:;
(3)若求的值.
22. 在平面直角坐标系中,O为坐标原点,抛物线与x轴交于点A,B,与y轴交于点C,点A的坐标为(2,0),点在抛物线上.
(1)求抛物线的表达式;
(2)如图①,点P在y轴上,且点P在点C的下方,若,求点P的坐标;
(3)如图②,E为线段CD上的动点,射线OE与线段AD交于点M,与抛物线交于点N,米的最大
分数(分)
60
70
80
90
100
人数
8
22
20
30
20
①
④
②
⑤
③
劳动时间/小时
频数
福建省厦门市同安第一中学2023-2024学年高一上学期期中数学试题(含答案): 这是一份福建省厦门市同安第一中学2023-2024学年高一上学期期中数学试题(含答案),共16页。试卷主要包含了选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
福建省厦门市厦门大学附属科技中学2023-2024学年高一上学期10月月考数学试题: 这是一份福建省厦门市厦门大学附属科技中学2023-2024学年高一上学期10月月考数学试题,共8页。
福建省宁德第一中学2023-2024学年高一上学期入学考试数学试题: 这是一份福建省宁德第一中学2023-2024学年高一上学期入学考试数学试题,共5页。












