

2021-2022学年北京十五中七年级(上)期中数学试卷【含解析】
展开1.(2分)下列各数﹣5、+3、﹣0.2、、0、﹣、﹣11、2.4中,负数有( )个.
A.3B.4C.5D.6
2.(2分)北京大兴国际机场航站楼形如展翅的凤凰,航站楼主体占地面积1030000平方米.将1030000用科学记数法表示为( )
A.10.3×105B.1.03×106C.1.03×107D.0.103×107
3.(2分)关于整式3x2﹣y+3xy3+x3﹣1,理解错误的是( )
A.它属于多项式
B.它是三次五项式
C.它的常数项是﹣1
D.它的最高次项的系数是3
4.(2分)有理数a,b在数轴上对应点的位置如图所示,下列说法中正确的是( )
A.a>bB.﹣a>bC.|a|>|b|D.a+b>0
5.(2分)索玛立方体拼搭是有名的数学游戏,它由七块立体图形组成,如图所示的这1~7号图形中,从正面看所得图形相同的有( )块.
A.2B.3C.4D.5
6.(2分)下列说法错误的是( )
A.负数的绝对值都是正数
B.除以一个数,等于乘这个数的倒数
C.有理数包括整数和分数
D.倒数等于它本身的数只有±1
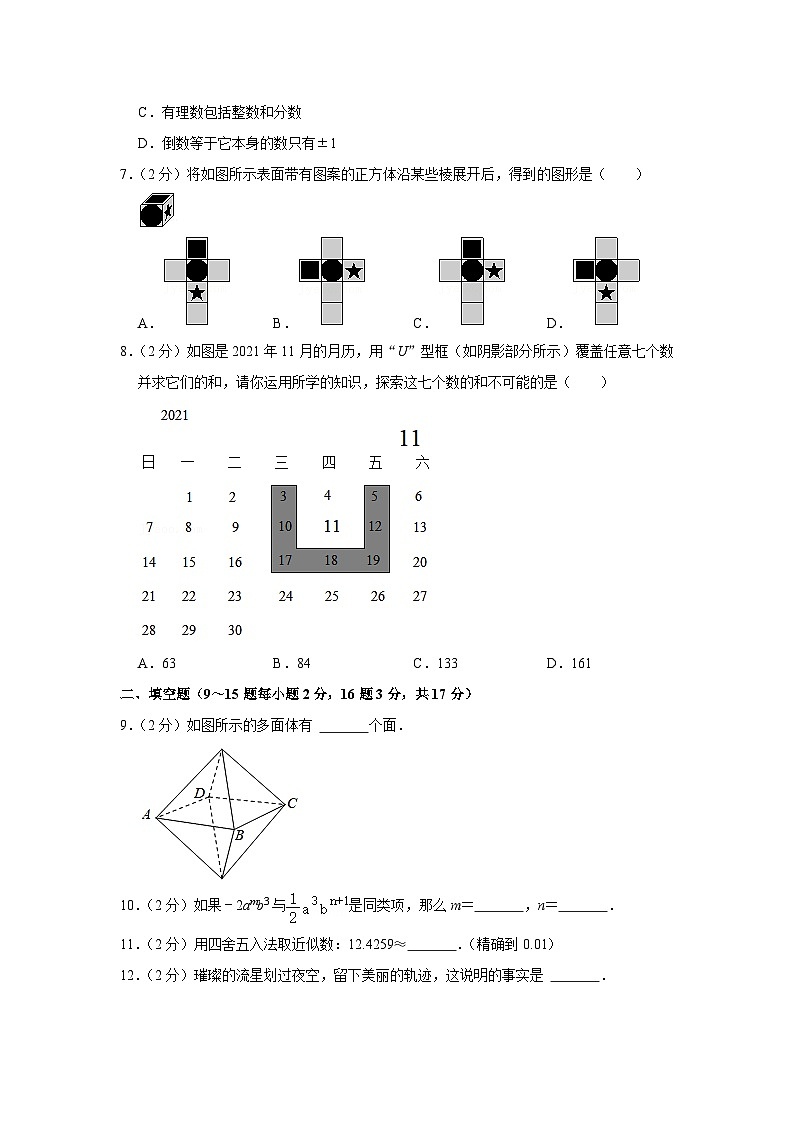
7.(2分)将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A.B.C.D.
8.(2分)如图是2021年11月的月历,用“U”型框(如阴影部分所示)覆盖任意七个数并求它们的和,请你运用所学的知识,探索这七个数的和不可能的是( )
A.63B.84C.133D.161
二、填空题(9~15题每小题2分,16题3分,共17分)
9.(2分)如图所示的多面体有 个面.
10.(2分)如果﹣2amb3与是同类项,那么m= ,n= .
11.(2分)用四舍五入法取近似数:12.4259≈ .(精确到0.01)
12.(2分)璀璨的流星划过夜空,留下美丽的轨迹,这说明的事实是 .
13.(2分)在计算“”时,甲同学的做法如下:
在上面的甲同学的计算过程中,开始出错的步骤是 (写出错误所在行的序号),这一步依据的运算法则应当是:同号两数相加, .
14.(2分)已知点A、B、C三个点在同一条直线上,若线段AB=10,BC=6,则线段AC= .
15.(2分)已知,如图1所示,将一个长为6a,宽为2b的长方形沿图中虚线裁剪成四个相同的小长方形,并按图2的方式拼出一个大正方形,则这个大正方形的周长是 .(用含a、b的代数式表示)
16.(3分)已知a为不等于1的有理数,我们把称为a的差倒数.例如:2的差倒数是,﹣1的差倒数是.已知a1=﹣3,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,以此类推……,则a2= ,a2021= .
三、解答题(共67分)
17.(24分)计算:
(1)6+(﹣15)﹣(﹣8);
(2);
(3);
(4);
(5);
(6).
18.(9分)化简:
(1)x+7x﹣5x;
(2);
(3)(﹣x+2x2+5)﹣(4x2﹣3﹣6x).
19.(6分)先化简,再求值:(5a2b﹣ab2)﹣3(ab2﹣a2b).其中.
20.(7分)作图题
(1)画数轴表示下列各数,并用“<”把他们从小到大排列起来.
﹣3,|﹣3|,,﹣(+4),0
< < < < .
(2)已知四点A、B、C、D,根据下列语句,在同一个图中画出图形.
第一步:画直线AB;
第二步:画射线AD、BC,交于点P;
第三步:连接BD,并延长线段BD到点E,使DE=BD;
第四步:连接CD,并将线段CD反向延长至点F,使CF=2CD.
21.(4分)如图:线段AB=14cm,C是AB上一点,且AC=9cm,O是AB的中点,求线段OC的长度.
22.(4分)有如图8筐白菜,以每筐25kg为标准,超过的千克数记作正数,不足的千克数记作负数,称后记录如下:
回答下列问题:
(1)这8筐白菜中,最接近标准的那筐白菜为 kg;
(2)以每筐25kg为标准,这8筐白菜总计超过多少千克或不足多少千克?
(3)计算这8筐白菜总计多少千克?
23.(6分)在小学学习正整数的加减时,我们会用“列竖式”的方法帮助计算.在进行整式的加减运算时也可以用类似的方法:如果把两个或者几个整式按同一字母降幂(或升幂)排列,并将各同类项对齐,就可以列竖式进行加减了,比如计算(﹣3x3+5x2﹣7)+(2x﹣3+3x2)就可以列竖式为:
根据上述阅读材料,解决下列问题:
已知:A=﹣3x﹣2x3+1+x4,B=2x3﹣4x2+x.
(1)将A按照x的降幂进行排列是: ;
(2)仿照上面的方法列竖式计算A+B;
(3)小丽说也可以用类似方法列竖式计算A﹣B,请你试试看;
(4)请写一个多项式C= ,使其与B的和是二次单项式.
24.(7分)我们知道,|a|的几何意义是:在数轴上数a对应的点到原点的距离,类似的,|x﹣y|的几何意义就是:数轴上数x,y对应点之间的距离.比如:2和5两点之间的距离可以用|2﹣5|表示,通过计算可以得到他们的距离是3.
(1)数轴上1和﹣3两点之间的距离可以用 表示,通过计算可以得到他们的距离是 .
(2)数轴上表示x和﹣3的两点A、B之间的距离可以表示为AB= ;如果AB=2,结合几何意义,那么x的值为 ;
(3)代数式|x﹣1|+|x+2|表示的几何意义是 ,该代数式的最小值是 .
附加题
25.(5分)附加题:已知数轴上两点A、B对应的数分别为﹣1、3,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A,点B的距离相等,求点P对应的数;
(2)数轴上是否存在点P,使点P到点A、点B的距离之和为6?若存在,请求出x的值;若不存在,说明理由;
(3)点A、点B分别以2个单位长度/分、1个单位长度/分的速度向右运动,同时点P以6个单位长度/分的速度从O点向左运动.当遇到A时,点P立即以同样的速度向右运动,并不停地往返于点A与点B之间,求当点A与点B重合时,点P所经过的总路程是多少?
26.(5分)给定一个十进制下的自然数x,对于x每个数位上的数,求出它除以2的余数,再把每一个余数按照原来的数位顺序排列,得到一个新的数,定义这个新数为原数x的“模二数”,记为M2(x).如M2(735)=111,M2(561)=101.
对于“模二数”的加法规定如下:将两数末位对齐,从右往左依次将相应数位上的数分别相加,规定:0与0相加得0;0与1相加得1;1与1相加得0,并向左边一位进1.如735、561的“模二数”111、101相加的运算过程如图所示,即M2(735)+M2(561)=1100.
根据以上材料,解决下列问题:
(1)M2(9653)的值为 ,M2(9653)+M2(58)的值为 ;
(2)如果两个自然数的和的“模二数”与它们的“模二数”的和相等,则称这两个数“模二相加不变”.
如M2(124)=100,M2(630)=010,
因为M2(124)+M2(630)=110,M2(124+630)=M2(754)=110,
所以M2(124+630)=M2(124)+M2(630),即124与630满足“模二相加不变”.
①判断12,65中哪个数与23“模二相加不变”,并说明理由;
②再写出一个与23“模二相加不变”的两位数.
2021-2022学年北京十五中七年级(上)期中数学试卷
参考答案与试题解析
一、选择题.(每小题2分,共16分)
1.(2分)下列各数﹣5、+3、﹣0.2、、0、﹣、﹣11、2.4中,负数有( )个.
A.3B.4C.5D.6
【分析】根据负数的定义,即负数为小于0的有理数,再判定负数的个数.
【解答】解:在﹣5、+3、﹣0.2、、0、﹣、﹣11、2.4中,负数有﹣5、﹣0.2、﹣、﹣11,共4个.
故选:B.
【点评】本题考查了正数和负数,解题的关键是掌握负数的定义.
2.(2分)北京大兴国际机场航站楼形如展翅的凤凰,航站楼主体占地面积1030000平方米.将1030000用科学记数法表示为( )
A.10.3×105B.1.03×106C.1.03×107D.0.103×107
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:数据1030000科学记数法表示为1.03×106.
故选:B.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
3.(2分)关于整式3x2﹣y+3xy3+x3﹣1,理解错误的是( )
A.它属于多项式
B.它是三次五项式
C.它的常数项是﹣1
D.它的最高次项的系数是3
【分析】先根据多项式的有关定义进行判断,不含字母的项叫做常数项.多项式中次数最高的项的次数叫做多项式的次数,如果一个多项式含有a个单项式,次数是b,那么这个多项式就叫b次a项式.
【解答】解:∵3x2﹣y+3xy3+x3﹣1的最高次项是3xy3,
次数为4,常数项为﹣1,它的最高次项的系数是3,
∴它是四次五项式,
∴A不符合题意;
B符合题意;
C不符合题意;
D不符合题意;
故选:B.
【点评】题考查了多项式,解题的关键是掌握多项式的有关概念,并注意符号的处理.
4.(2分)有理数a,b在数轴上对应点的位置如图所示,下列说法中正确的是( )
A.a>bB.﹣a>bC.|a|>|b|D.a+b>0
【分析】根据有理数a,b在数轴上对应点的位置,可知,a<0,b>0,且|a|<|b|,再根据有理数加法的计算方法得出答案.
【解答】解:根据有理数a,b在数轴上对应点的位置,可知a<0,b>0,且|a|<|b|,
∴a+b>0,
故选:D.
【点评】考查数轴表示数的意义,根据数轴上两点位置,确定各个数的符号和绝对值是得出正确结论的前提.
5.(2分)索玛立方体拼搭是有名的数学游戏,它由七块立体图形组成,如图所示的这1~7号图形中,从正面看所得图形相同的有( )块.
A.2B.3C.4D.5
【分析】根据从正面看得到的图形是主视图,可得答案.
【解答】解:从正面看,1号,6号,7号的主视图相同,底层均是两个小正方形,上层右边是一个小正方形,
所以从正面看所得图形相同的有3块.
故选:B.
【点评】本题考查了简单几何体的三视图,从正面看得到的图形是主视图,熟悉常见几何体的三视图是解题关键.
6.(2分)下列说法错误的是( )
A.负数的绝对值都是正数
B.除以一个数,等于乘这个数的倒数
C.有理数包括整数和分数
D.倒数等于它本身的数只有±1
【分析】利用有理数的除法法则,有理数定义,绝对值,倒数的性质判断即可.
【解答】解:A、负数的绝对值都是正数,不符合题意;
B、除以一个非0的数,等于乘以这个数的倒数,符合题意;
C、有理数包括整数和分数,不符合题意;
D、倒数等于它本身的数只有±1,不符合题意.
故选:B.
【点评】此题考查了有理数的除法,正数和负数,有理数,绝对值,以及倒数,熟练掌握各自的性质是解本题的关键.
7.(2分)将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A.B.C.D.
【分析】根据平面图形的折叠及立体图形的表面展开图的特点解题.注意带图案的三个面相交于一点.
【解答】解:由原正方体知,带图案的三个面相交于一点,而通过折叠后A、B都不符合,且D折叠后图案的位置正好相反,所以能得到的图形是C.
故选:C.
【点评】此题主要考查了几何体的展开图,解决此类问题,要充分考虑带有各种符号的面的特点及位置.
8.(2分)如图是2021年11月的月历,用“U”型框(如阴影部分所示)覆盖任意七个数并求它们的和,请你运用所学的知识,探索这七个数的和不可能的是( )
A.63B.84C.133D.161
【分析】设包括“U”型框内部两个数在内的九个数正中间的数为x,分别用含x的代数式表示“U”型框覆盖的七个数并求出表示它们的和的代数式,另其分别等于问题答案中的四个数,求出相应的x值再分别进行检验,即可得出问题的答案.
【解答】解:设包括“U”型框内部两个数在内的九个数正中间的数为x,
则“U”型框覆盖的七个数分别是x﹣8,x﹣6,x﹣1,x+1,x+6,x+7,x+8,
∴x﹣8+x﹣6+x﹣1+x+1+x+6+x+7+x+8=7x+7,
由7x+7=63得x=8,此时“U”型框只覆盖6个数,不符合题意;
由7x+7=84得x=11,符合题意;
由7x+7=133得x=18,符合题意;
由7x+7=161得x=22,符合题意,
∴这七个数的和不可能是63,
故选:A.
【点评】此题考查解一元一次方程、列一元一次方程解应用题、数字问题的求解等知识与方法,适当设未知数并且正确地用代数式表示“U”型框覆盖的七个数的和是解题的关键.
二、填空题(9~15题每小题2分,16题3分,共17分)
9.(2分)如图所示的多面体有 8 个面.
【分析】根据图形可得答案.
【解答】解:根据图形可知:共有8个面.
故答案为:8.
【点评】此题考查的是立体图形,正确数出面的个数是解决此题的关键.
10.(2分)如果﹣2amb3与是同类项,那么m= 3 ,n= 2 .
【分析】根据同类项的定义即可求得m、n的值.
【解答】解:因为﹣2amb3与a3bn+1是同类项,
所以m=3,n+1=3,
所以n=2.
故答案为:3,2.
【点评】本题考查同类项的定义.解题的关键是掌握同类项的定义:所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.要注意同类项定义中的两个“相同”:所含字母相同,并且相同字母的指数也相同,是易混点,因此成了中考的常考点.
11.(2分)用四舍五入法取近似数:12.4259≈ 12.43 .(精确到0.01)
【分析】把千分位上的数字5进行四舍五入即可.
【解答】解:12.4259≈12.43.
故答案为:12.43.
【点评】本题考查了近似数:“精确到第几位”是精确度的常用的表示形式.
12.(2分)璀璨的流星划过夜空,留下美丽的轨迹,这说明的事实是 点动成线 .
【分析】根据点、线、面、体的关系进行判断即可.
【解答】解:流星可看作“点”,
流星划过夜空,留下美丽的轨迹,
这说明的事实点动成线,
故答案为:点动成线.
【点评】本题考查点、线、面、体,理解“点动成线”是正确判断的关键.
13.(2分)在计算“”时,甲同学的做法如下:
在上面的甲同学的计算过程中,开始出错的步骤是 ② (写出错误所在行的序号),这一步依据的运算法则应当是:同号两数相加, 取相同的符号,并把绝对值相加 .
【分析】根据有理数的加减混合运算,逐步去判断即可.,
【解答】解:因为:=﹣4,
所以开始出错的步骤是:②,
这一步依据的运算法则应当是:同号两数相加,取相同的符号,并把绝对值相加,
故答案为:②;取相同的符号,并把绝对值相加.
【点评】本题考查了有理数的加减混合运算,学生必须熟练掌握运算法则是解题的关键.
14.(2分)已知点A、B、C三个点在同一条直线上,若线段AB=10,BC=6,则线段AC= 16或4 .
【分析】分两种情况,点C在点B的右侧,点C在点B左侧.
【解答】解:当点C在点B的右侧时,如图:
所以:AC=AB+BC=16,
当点C在点B左侧时,如图:
所以:AC=AB﹣BC=4,
故答案为:16或4.
【点评】本题考查了两点间的距离,同时本题渗透了分类讨论的数学思想.
15.(2分)已知,如图1所示,将一个长为6a,宽为2b的长方形沿图中虚线裁剪成四个相同的小长方形,并按图2的方式拼出一个大正方形,则这个大正方形的周长是 12a+4b .(用含a、b的代数式表示)
【分析】先分别求得每个小长方形的长与宽,然后求得正方形的边长,从而求其周长.
【解答】解:如图:
由题意可得:AB=DE==3a,AC=EF==b,
∴大正方形的的边长DF=DE+EF=3a+b,
∴大正方形的周长为4(3a+b)=12a+4b,
故答案为:12a+4b.
【点评】本题考查整式的加减的应用,准确识图,掌握合并同类项(系数相加,字母及其指数不变)的运算法则是解题关键.
16.(3分)已知a为不等于1的有理数,我们把称为a的差倒数.例如:2的差倒数是,﹣1的差倒数是.已知a1=﹣3,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,以此类推……,则a2= ,a2021= .
【分析】根据定义分别求出a2=,a3=,a4=﹣3,从而发现每3个数循环一次,则可知a2021=a2=.
【解答】解:∵a1=﹣3,
∴a2==,
a3==,
a4==﹣3,
…,
∴每3个数循环一次,
∵2021÷3=673…2,
∴a2021=a2=,
故答案为:,.
【点评】本题考查数字的变化规律,能够通过计算,找到数字的循环规律是解题的关键.
三、解答题(共67分)
17.(24分)计算:
(1)6+(﹣15)﹣(﹣8);
(2);
(3);
(4);
(5);
(6).
【分析】(1)先把减法转化为加法,然后有理数的加法法则计算即可;
(2)先把除法转化为乘法、然后根据有理数的乘法法则计算即可;
(3)先去小括号,再去中括号,最后计算计算即可;
(4)根据乘法分配律计算即可;
(5)先算乘方、再算乘除法、最后算减法即可;
(6)先算乘方、再算括号内的式子,最后计算括号外的乘法和减法即可.
【解答】解:(1)6+(﹣15)﹣(﹣8)
=6+(﹣15)+8
=﹣1;
(2)
=
=;
(3)
=+()
=
=
=
=;
(4)
=36×+36×﹣36×
=4+6﹣27
=﹣17;
(5)
=
=8×(﹣6)﹣1
=﹣48﹣1
=﹣49;
(6)
=
=0﹣8+(﹣3)
=﹣11.
【点评】本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的运算法则和运算顺序,注意乘法分配律的应用.
18.(9分)化简:
(1)x+7x﹣5x;
(2);
(3)(﹣x+2x2+5)﹣(4x2﹣3﹣6x).
【分析】(1)原式合并同类项进行化简;
(2)原式去括号进行化简;
(3)原式去括号,合并同类项进行化简.
【解答】解:(1)原式=(1+7﹣5)x
=3x;
(2)原式=﹣×9y+×3
=﹣3y+1;
(3)原式=﹣x+2x2+5﹣4x2+3+6x
=﹣2x2+5x+8.
【点评】本题考查整式的加减,掌握合并同类项(系数相加,字母及其指数不变)和去括号的运算法则(括号前面是“+”号,去掉“+”号和括号,括号里的各项不变号;括号前面是“﹣”号,去掉“﹣”号和括号,括号里的各项都变号)是解题关键.
19.(6分)先化简,再求值:(5a2b﹣ab2)﹣3(ab2﹣a2b).其中.
【分析】先去括号,再合并同类项;根据绝对值和偶次方的非负性求出a和b的值,再代入化简结果即可.
【解答】解:原式=5a2b﹣ab2﹣3ab2+3a2b
=8a2b﹣4ab2,
∵,
∴.
代入原式=
=
=
=.
【点评】本题考查整式的加减—化简求值,掌握去括号法则和合并同类项法则是解题关键.
20.(7分)作图题
(1)画数轴表示下列各数,并用“<”把他们从小到大排列起来.
﹣3,|﹣3|,,﹣(+4),0
﹣(+4) < ﹣3 < 0 < < |﹣3| .
(2)已知四点A、B、C、D,根据下列语句,在同一个图中画出图形.
第一步:画直线AB;
第二步:画射线AD、BC,交于点P;
第三步:连接BD,并延长线段BD到点E,使DE=BD;
第四步:连接CD,并将线段CD反向延长至点F,使CF=2CD.
【分析】(1)先画出数轴,再在数轴上找到各数对应的点即可;
(2)根据画图的步骤即可画出图形.
【解答】解:(1)在数轴上表示如图所示:
∴﹣(+4)<﹣3<0<<|﹣3|;
(2)如图即为所求.
【点评】本题考查了直线,射线,线段,数轴,相反数,绝对值,有理数的大小比较,这些都是学生必备的数学基本功.
21.(4分)如图:线段AB=14cm,C是AB上一点,且AC=9cm,O是AB的中点,求线段OC的长度.
【分析】在一条直线或线段上的线段的加减运算和倍数运算,首先明确线段间的相互关系,最好准确画出几何图形,再根据题意进行计算.
【解答】解:∵点O是线段AB的中点,AB=14cm
∴AO=AB=7cm
∴OC=AC﹣AO
=9cm﹣7cm
=2cm.
答:线段OC的长度为2cm.
【点评】利用中点性质转化线段之间的倍分关系是解题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.
22.(4分)有如图8筐白菜,以每筐25kg为标准,超过的千克数记作正数,不足的千克数记作负数,称后记录如下:
回答下列问题:
(1)这8筐白菜中,最接近标准的那筐白菜为 24.5 kg;
(2)以每筐25kg为标准,这8筐白菜总计超过多少千克或不足多少千克?
(3)计算这8筐白菜总计多少千克?
【分析】(1)根据绝对值的意义,绝对值越小越接近标准,可得答案;
(2)根据有理数的加法运算,可得答案;
(3)用25×8,再加上(2)的结果数即可.
【解答】解:(1)在记录的数中,﹣0.5的绝对值最小,
所以这8筐白菜中,最接近标准的那筐白菜为:25﹣0.5=24.5(千克),
故答案为:24.5;
(2)1.5+(﹣3)+2+(﹣0.5)+1+(﹣2)+(﹣2)+(﹣2.5)=﹣5.5(千克),
答:不足5.5千克;
(3)25×8﹣5.5=194.5(千克),
答:总计194.5千克.
【点评】此题主要考查了正负数的意义以及有理数的混合运算,掌握有理数的运算法则是解答本题的关键.
23.(6分)在小学学习正整数的加减时,我们会用“列竖式”的方法帮助计算.在进行整式的加减运算时也可以用类似的方法:如果把两个或者几个整式按同一字母降幂(或升幂)排列,并将各同类项对齐,就可以列竖式进行加减了,比如计算(﹣3x3+5x2﹣7)+(2x﹣3+3x2)就可以列竖式为:
根据上述阅读材料,解决下列问题:
已知:A=﹣3x﹣2x3+1+x4,B=2x3﹣4x2+x.
(1)将A按照x的降幂进行排列是: x4﹣2x3﹣3x+1 ;
(2)仿照上面的方法列竖式计算A+B;
(3)小丽说也可以用类似方法列竖式计算A﹣B,请你试试看;
(4)请写一个多项式C= ﹣2x3﹣x ,使其与B的和是二次单项式.
【分析】(1)根据降幂排列直接排列即可;
(2)列算式,再进行计算即可;
(3)列算式,再进行计算即可;
(4)假设给定一个二次单项式,再作差即可.
【解答】解:(1)根据题意可得,x4﹣2x3﹣3x+1;
故答案为:x4﹣2x3﹣3x+1;
(2)列式如下:
A+B=x4﹣4x2﹣2x+1;
(3)列示如下:
A﹣B=x4﹣4x3+4x2﹣4x+1;
(4)设这个二次单项式为﹣4x2,
则C=﹣4x2﹣(2x3﹣4x2+x)=﹣2x3﹣x;
∴答案不唯一,如﹣2x3﹣x.
【点评】此题主要考查了整式的加减,正确理解题意运用竖式计算是解题关键.
24.(7分)我们知道,|a|的几何意义是:在数轴上数a对应的点到原点的距离,类似的,|x﹣y|的几何意义就是:数轴上数x,y对应点之间的距离.比如:2和5两点之间的距离可以用|2﹣5|表示,通过计算可以得到他们的距离是3.
(1)数轴上1和﹣3两点之间的距离可以用 |1﹣(﹣3)| 表示,通过计算可以得到他们的距离是 4 .
(2)数轴上表示x和﹣3的两点A、B之间的距离可以表示为AB= |x﹣(﹣3)| ;如果AB=2,结合几何意义,那么x的值为 ﹣1或﹣5 ;
(3)代数式|x﹣1|+|x+2|表示的几何意义是 数轴上表示数x的点到1和﹣2两点的距离的和 ,该代数式的最小值是 3 .
【分析】(1)根据题目中的几何意义可以直接得到1和﹣3两点之间的距离的表示方法,再计算即可;
(2)根据题目中的几何意义可以直接得到x和﹣3两点之间的距离的表示方法,再解关于x的绝对值方程|x﹣(﹣3)|=2即可;
(3)根据两点之间距离的几何意义,结合数轴发现x在1和﹣2之间时,代数式的值最小.
【解答】解:(1)数轴上1和﹣3两点之间的距离可以表示为|1﹣(﹣3)|;
∴1和﹣3两点之间的距离是4.
故答案为:|1﹣(﹣3)|;4.
(2)数轴上表示x和﹣3的两点A、B之间的距离可以表示AB=|x﹣(﹣3)|;
∵AB=2,
∴|x﹣(﹣3)|=2,
∴x=﹣1或﹣5.
故答案为:|x﹣(﹣3)|;﹣1或﹣5.
(3)代数式|x﹣1|+|x+2|表示的几何意义是数轴上表示数x的点到1和﹣2两点的距离的和;
x位于﹣1到2之间时它们的距离和有最小值为3.
故答案为:数轴上表示数x的点到1和﹣2两点的距离的和;3.
【点评】此题综合考查了数轴、绝对值的有关内容,用几何方法借助数轴来求解,体现了数形结合思想.
附加题
25.(5分)附加题:已知数轴上两点A、B对应的数分别为﹣1、3,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A,点B的距离相等,求点P对应的数;
(2)数轴上是否存在点P,使点P到点A、点B的距离之和为6?若存在,请求出x的值;若不存在,说明理由;
(3)点A、点B分别以2个单位长度/分、1个单位长度/分的速度向右运动,同时点P以6个单位长度/分的速度从O点向左运动.当遇到A时,点P立即以同样的速度向右运动,并不停地往返于点A与点B之间,求当点A与点B重合时,点P所经过的总路程是多少?
【分析】(1)若点P对应的数与﹣1、3差的绝对值相等,则点P到点A,点B的距离相等.
(2)根据当P在A的左侧以及当P在B的右侧分别求出即可;
(3)设经过a分钟点A与点B重合,根据点A比点B运动的距离多4,列出方程,求出a的值,即为点P运动的时间,再乘以点P运动的速度,可得点P经过的总路程.
【解答】解:(1)∵1﹣(﹣1)=2,2的绝对值是2,1﹣3=﹣2,﹣2的绝对值是2,
∴点P对应的数是1.
(2)当P在AB之间,PA+PB=4(不可能有)
当P在A的左侧,PA+PB=﹣1﹣x+3﹣x=6,得x=﹣2
当P在B的右侧,PA+PB=x﹣(﹣1)+x﹣3=6,得x=4
故点P对应的数为﹣2或4;
(3)解:设经过a分钟点A与点B重合,根据题意得:
2a=4+a,
解得a=4.
则6a=24.
答:点P所经过的总路程是24个单位长度.
【点评】本题考查了绝对值、路程问题、一元一次方程等知识,解题的关键是理解题意,学会构建方程解决问题,属于中考常考题型.
26.(5分)给定一个十进制下的自然数x,对于x每个数位上的数,求出它除以2的余数,再把每一个余数按照原来的数位顺序排列,得到一个新的数,定义这个新数为原数x的“模二数”,记为M2(x).如M2(735)=111,M2(561)=101.
对于“模二数”的加法规定如下:将两数末位对齐,从右往左依次将相应数位上的数分别相加,规定:0与0相加得0;0与1相加得1;1与1相加得0,并向左边一位进1.如735、561的“模二数”111、101相加的运算过程如图所示,即M2(735)+M2(561)=1100.
根据以上材料,解决下列问题:
(1)M2(9653)的值为 1011 ,M2(9653)+M2(58)的值为 1101 ;
(2)如果两个自然数的和的“模二数”与它们的“模二数”的和相等,则称这两个数“模二相加不变”.
如M2(124)=100,M2(630)=010,
因为M2(124)+M2(630)=110,M2(124+630)=M2(754)=110,
所以M2(124+630)=M2(124)+M2(630),即124与630满足“模二相加不变”.
①判断12,65中哪个数与23“模二相加不变”,并说明理由;
②再写出一个与23“模二相加不变”的两位数.
【分析】(1)根据定义运算即可;
(2)分别求出M2(12)=10,M2(65)=01,M2(23)=01,再求出M2(12)+M2(23)=11,M2(65)+M2(23)=10,M2(12+23)=11,M2(65+23)=00,
即可求解;
(3)答案不唯一,只需所求数的“模二数”是10即可.
【解答】解:(1)M2(9653)=1011,M2(58)=10,
∴M2(9653)+M2(58)=1011+10=1101,
故答案为:1011,1101;
(2)①∵M2(12)=10,M2(65)=01,M2(23)=01,
∴M2(12)+M2(23)=10+01=11,
M2(65)+M2(23)=01+01=10,
∵M2(12+23)=M2(35)=11,M2(65+23)=M2(88)=00,
∴M2(12)+M2(23)=M2(12+23),
∴12与23“模二相加不变”;
②∵M2(34)=10,
∴M2(34)+M2(23)=10+01=11,M2(34+23)=M2(57)=11,
∴M2(34)+M2(23)=M2(34+23),
∴34与23“模二相加不变”,(答案不唯一,如55,97等均可).
【点评】本题考查新定义,理解定义内容,能将定义与已学内容相结合是解题的关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2022/9/29 20:48:23;用户:笑涵数学;邮箱:15699920825;学号:36906111
2021-2022学年北京三十五中七年级(上)期中数学试卷【含解析】: 这是一份2021-2022学年北京三十五中七年级(上)期中数学试卷【含解析】,共16页。试卷主要包含了单项选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2021-2022学年北京七中七年级(上)期中数学试卷【含解析】: 这是一份2021-2022学年北京七中七年级(上)期中数学试卷【含解析】,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年北京八十中七年级(上)期中数学试卷【含解析】: 这是一份2021-2022学年北京八十中七年级(上)期中数学试卷【含解析】,共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












