2022-2023学年北京市昌平区回天高未融合学区九年级（上）期中数学试卷【含解析】

这是一份2022-2023学年北京市昌平区回天高未融合学区九年级（上）期中数学试卷【含解析】，共32页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。

1．（2分）已知3a＝2b（ab≠0），则下列各式正确的是（ ）
A．B．C．D．
2．（2分）抛物线y＝（x﹣1）2+2的对称轴是（ ）
A．x＝﹣1B．x＝1C．x＝﹣2D．x＝2
3．（2分）生活中到处可见黄金分割的美．如图，在设计人体雕像时，使雕像的腰部以下a与全身b的高度比值接近0.618，可以增加视觉美感．若图中b为2米，则a约为（ ）
A．1.24米B．1.38米C．1.42米D．1.62米
4．（2分）将抛物线y＝﹣2x2先向右平移1个单位，再向上平移3个单位，得到的抛物线是（ ）
A．y＝﹣2（x+1）2+3B．y＝﹣2（x﹣1）2﹣3
C．y＝﹣2（x+1）2﹣3D．y＝﹣2（x﹣1）2+3
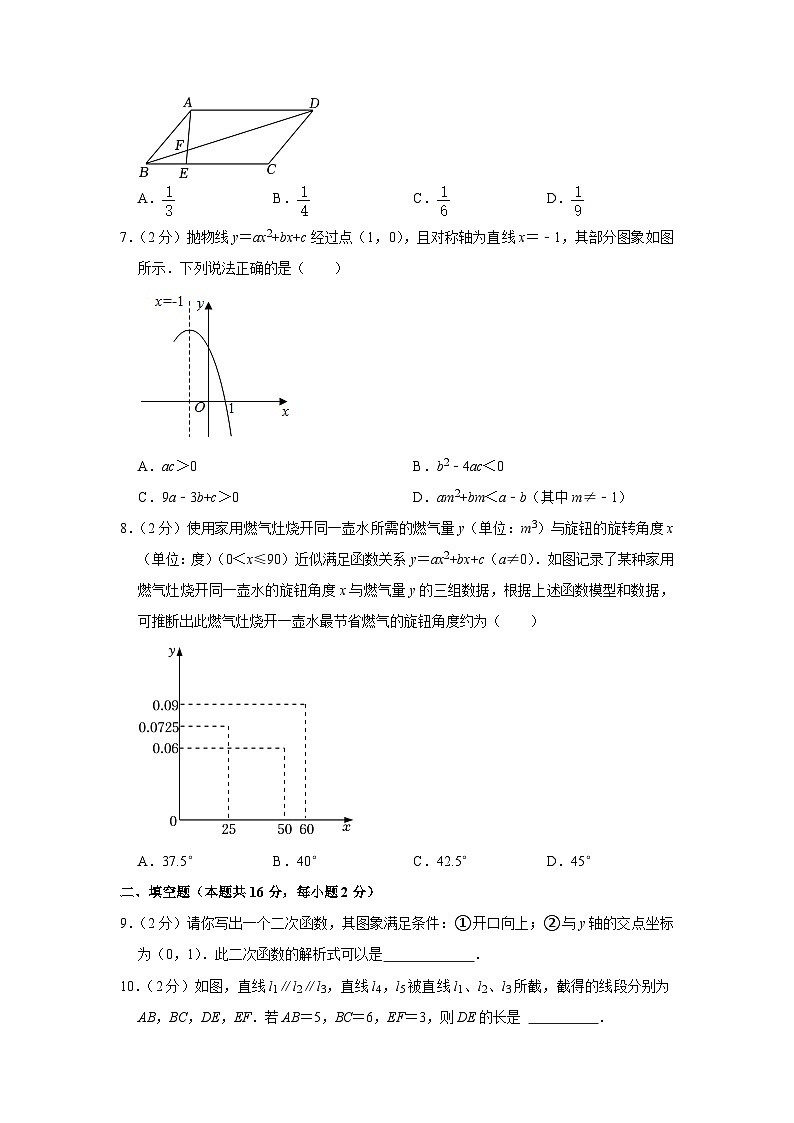
5．（2分）如图，已知∠A＝∠D，请你再添加一个条件________使得△ABC∽△DEF．则下列选项不成立的是（ ）
A．∠B＝∠EB．∠C＝∠FC．D．
6．（2分）如图，在平行四边形ABCD中，E是边BC上3等分点，AE交BD于点F．则△BEF与△DAF的面积比为（ ）
A．B．C．D．
7．（2分）抛物线y＝ax2+bx+c经过点（1，0），且对称轴为直线x＝﹣1，其部分图象如图所示．下列说法正确的是（ ）
A．ac＞0B．b2﹣4ac＜0
C．9a﹣3b+c＞0D．am2+bm＜a﹣b（其中m≠﹣1）
8．（2分）使用家用燃气灶烧开同一壶水所需的燃气量y（单位：m3）与旋钮的旋转角度x（单位：度）（0＜x≤90）近似满足函数关系y＝ax2+bx+c（a≠0）．如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为（ ）
A．37.5°B．40°C．42.5°D．45°
二、填空题（本题共16分，每小题2分）
9．（2分）请你写出一个二次函数，其图象满足条件：①开口向上；②与y轴的交点坐标为（0，1）．此二次函数的解析式可以是 ．
10．（2分）如图，直线l1∥l2∥l3，直线l4，l5被直线l1、l2、l3所截，截得的线段分别为AB，BC，DE，EF．若AB＝5，BC＝6，EF＝3，则DE的长是 ．
11．（2分）将二次函数y＝x2+2x﹣1化为y＝（x﹣h）2+k的形式，结果为y＝ ．
12．（2分）如图，△AEC中，AE∥BD，CD＝8，DE＝4，那么＝ ．
13．（2分）已知二次函数y＝（x﹣2）2+3，若点A（0，y1）和B（3，y2）在此函数图象上，则y1与y2的大小关系是y1 y2．（填“＞”，“＜”或“＝”）
14．（2分）已知二次函数y＝ax2+bx+c（a≠0）的部分图象如图所示，则关于x的一元二次方程ax2+bx+c＝0（a≠0）的解为 ．
15．（2分）《九章算术》中记载了一种测量井深的方法．如图所示，在井口B处立一根垂直于井口的木杆BD，从木杆的顶端D观察井水水岸C，视线DC与井口的直径AB交于点E，如果测得AB＝1.8米，BD＝1米，BE＝0.2米，那么AC为 米．
16．（2分）如图，抛物线y＝﹣x2+2．将该抛物线在x轴和x轴上方的部分记作C1，将x轴下方的部分沿x轴翻折后记作C2，C1和C2构成的图形记作C3．
关于图形C3，给出如下四个结论：①图形C3关于y轴成轴对称；②图形C3有最小值，且最小值为0；③当x＞0时，图形C3的函数值都是随着x的增大而增大的；④当﹣2≤x≤2时，图形C3恰好经过5个整点（即横、纵坐标均为整数的点）．以上四个结论中，所有正确结论的序号是 ．
三、解答题（本题共12道小题，第17-22题，每小题5分，第23-26题，每小题5分，第27，28题，每小题5分，共68分）
17．（5分）已知二次函数y＝x2﹣4．
（1）求该二次函数图象的对称轴与顶点坐标；
（2）求该二次函数图象与x轴、y轴的交点．
18．（5分）如图，在△ABC中，∠C＝90°，点D是AC上一点，DE⊥AB于点E．求证：△ABC∽△ADE．
19．（5分）如图，函数y＝﹣x2+bx+c的图象经过点A，B，C．求此函数表达式．
20．（5分）如图是边长为1的正方形网格，△A1B1C1的顶点均在格点上．
（1）在该网格中画出△A2B2C2（△A2B2C2的顶点均在格点上），使△A2B2C2∽△A1B1C1；
（2）说明△A2B2C2和△A1B1C1相似的依据．
21．（5分）一个二次函数图象上部分点的横坐标x，纵坐标y的对应值如下表：
（1）求这个二次函数的表达式；
（2）求m的值；
（3）在给定的直角坐标系中，画出这个函数的图象；
（4）根据图象，写出当y＜0时，x的取值范围．
22．（5分）已知：如图，在Rt△ABC中，∠ACB＝90°，CD是AB边上的高．
（1）求证：△ABC∽△CBD；
（2）如果AD＝4，BD＝3，求BC的长．
23．（6分）如图，在平行四边形ABCD中，点E在BC边上，点F在DC的延长线上，且∠AEB＝∠F．
（1）求证：△ABE∽△ECF；
（2）若AB＝5，CE＝6，BE＝2，求FD的长．
24．（6分）2022年北京冬奥会即将召开，激起了人们对冰雪运动的极大热情．如图是某跳台滑雪训练场的横截面示意图，取某一位置的水平线为x轴，过跳台终点A作水平线的垂线为y轴，建立平面直角坐标系．图中的抛物线C1：y＝﹣x+1近似表示滑雪场地上的一座小山坡，某运动员从点O正上方4米处的A点滑出，滑出后沿一段抛物线C2：y＝﹣+bx+c运动．
（1）当运动员运动到离A处的水平距离为4米时，离水平线的高度为8米，求抛物线C2的函数解析式（不要求写出自变量x的取值范围）；
（2）在（1）的条件下，当运动员运动水平线的水平距离为多少米时，运动员与小山坡的竖直距离为1米？
25．（6分）学习完《相似形》一章之后，数学兴趣小组利用相似三角形的有关知识测量校园内一棵树高，他们的方法如下：
如图，为了测量操场上一棵大树的高度，小英拿来一面镜子，平放在离树根部5m的地面上，然后她沿着树根和镜子所在的直线后退，当她后退1m时，正好在镜中看见树的顶端．小英估计自己的眼睛到地面的距离为1.6m，则可测得大树的高度．
（1）请你根据上述方法求出树高；
（2）请你设计一个其他的测量方案，并简述方案．
26．（6分）在平面直角坐标系xOy中，已知抛物线y＝ax2﹣2ax+4（a＞0）．
（1）求该抛物线的对称轴和顶点坐标（用含a的代数式表示）；
（2）如果该抛物线的顶点恰好在x轴上，求它的表达式；
（3）如果A（m﹣1，y1），B（m，y2），C（m+2，y3）三点均在抛物线y＝ax2﹣2ax+4上，且总有y1＞y3＞y2，结合图象，直接写出m的取值范围．
27．（7分）如图，O为四边形ABCD内一点，E为AB的中点，OA＝OD，OB＝OC，∠AOB+∠COD＝180°．
（1）若∠BOE＝∠BAO，AB＝，求OB的长；
（2）用等式表示线段OE和CD之间的关系，并证明．
28．（7分）对某一个函数给出如下定义：如果存在实数M，对于任意的函数值y，都满足y≤M，那么称这个函数是有上界函数．在所有满足条件的M中，其最小值称为这个函数的上确界．例如，图中的函数y＝﹣（x﹣3）2+2是有上界函数，其上确界是2．
（1）函数①y＝x2+2x+1和②y＝2x﹣3（x≤2）中是有上界函数的为 （只填序号即可），其上确界为 ；
（2）如果函数y＝﹣x+2（a≤x≤b，b＞a）的上确界是b，且这个函数的最小值不超过2a+1，求a的取值范围；
（3）如果函数y＝x2﹣2ax+2（1≤x≤5）是以3为上确界的有上界函数，求实数a的值．
2022-2023学年北京市昌平区回天高未融合学区九年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有一个．
1．（2分）已知3a＝2b（ab≠0），则下列各式正确的是（ ）
A．B．C．D．
【分析】根据内项之积等于外项之积对各选项进行判断．
【解答】解：∵3a＝2b，
∴＝，＝，所以A选项符合题意，B、C、D选项不符合题意．
故选：A．
【点评】本题考查了比例的性质：熟练掌握比例的性质（内项之积等于外项之积；合比性质；分比性质；合分比性质；等比性质）是解决问题的关键．
2．（2分）抛物线y＝（x﹣1）2+2的对称轴是（ ）
A．x＝﹣1B．x＝1C．x＝﹣2D．x＝2
【分析】直接根据抛物线顶点式即可求得．
【解答】解：∵抛物线y＝（x﹣1）2+2，
∴对称轴为直线x＝1．
故选：B．
【点评】本题考查的是二次函数的性质，即二次函数y＝ax2+bx+c（a≠0）的顶点坐标是（﹣，），对称轴直线x＝﹣．
3．（2分）生活中到处可见黄金分割的美．如图，在设计人体雕像时，使雕像的腰部以下a与全身b的高度比值接近0.618，可以增加视觉美感．若图中b为2米，则a约为（ ）
A．1.24米B．1.38米C．1.42米D．1.62米
【分析】根据雕像的腰部以下a与全身b的高度比值接近0.618，因为图中b为2米，即可求出a的值．
【解答】解：∵雕像的腰部以下a与全身b的高度比值接近0.618，
∴≈0.618，
∵b为2米，
∴a约为1.24米．
故选：A．
【点评】本题考查了黄金分割，解决本题的关键是掌握黄金分割定义．
4．（2分）将抛物线y＝﹣2x2先向右平移1个单位，再向上平移3个单位，得到的抛物线是（ ）
A．y＝﹣2（x+1）2+3B．y＝﹣2（x﹣1）2﹣3
C．y＝﹣2（x+1）2﹣3D．y＝﹣2（x﹣1）2+3
【分析】由抛物线平移不改变二次项系数a的值，根据点的平移规律“左加右减，上加下减”可知移动后的顶点坐标，再由顶点式可求移动后的函数表达式．
【解答】解：原抛物线的顶点为（0，0），向右平移1个单位，再向上平移3个单位后，那么新抛物线的顶点为：（1，3）．
可设新抛物线的解析式为y＝﹣2（x﹣h）2+k，代入得y＝﹣2（x﹣1）2+3．
故选：D．
【点评】本题考查了二次函数图象与几何变换．解决本题的关键是得到新抛物线的顶点坐标．
5．（2分）如图，已知∠A＝∠D，请你再添加一个条件________使得△ABC∽△DEF．则下列选项不成立的是（ ）
A．∠B＝∠EB．∠C＝∠FC．D．
【分析】根据相似三角形的判定方法即可得以解决．
【解答】解：∵∠A＝∠D，
∴当添加条件∠B＝∠E时，则△ABC∽△DEF，故选项A不符合题意；
当添加条件∠C＝∠F时，则△ABC∽△DEF，故选项B不符合题意；
当添加条件时，则△ABC∽△DEF，故选项C不符合题意；
当添加条件时，则△BC和△DEF不一定相似，故选项D符合题意；
故选：D．
【点评】本题考查相似三角形的判定，解答本题的关键是明确题意，利用三角形相似的判定方法解答．
6．（2分）如图，在平行四边形ABCD中，E是边BC上3等分点，AE交BD于点F．则△BEF与△DAF的面积比为（ ）
A．B．C．D．
【分析】利用平行四边形的性质以及相似三角形的判定得出△BEF∽△DAF，进而求出答案．
【解答】解：在平行四边形ABCD中，E是BC上的3等分点，
∴AD∥BE，AD＝BC，BE＝AD，
∴△BEF∽△DAF，
∴＝（）2＝（）2＝，
故选：D．
【点评】此题主要考查了平行四边形的性质以及相似三角形的判定与性质，得出△BEF∽△DAF是解题关键．
7．（2分）抛物线y＝ax2+bx+c经过点（1，0），且对称轴为直线x＝﹣1，其部分图象如图所示．下列说法正确的是（ ）
A．ac＞0B．b2﹣4ac＜0
C．9a﹣3b+c＞0D．am2+bm＜a﹣b（其中m≠﹣1）
【分析】利用抛物线开口方向得到a＜0，利用抛物线与y轴的交点位置得到c＞0，则可对A选项进行判断；利用抛物线的对称性得到抛物线与x轴的另一个交点坐标为（﹣3，0），则根据判别式的意义可对B选项进行判断；由于x＝﹣3时，y＝0，则可对C选项错误；根据二次函数的最值问题可对D选项进行判断．
【解答】解：∵抛物线开口向下，
∴a＜0，
∵抛物线与y轴的交点在y轴的正半轴上，
∴c＞0，
∴ac＜0，所以A选项错误；
∵抛物线的对称轴为直线x＝﹣1，抛物线与x轴的一个交点坐标为（1，0），
∴抛物线与x轴的另一个交点坐标为（﹣3，0），
∴Δ＝b2﹣4ac＞0，所以B选项错误；
∵x＝﹣3时，y＝0，
∴9a﹣3b+c＝0，所以C选项错误；
∵x＝﹣1时，y有最大值，
∴am2+bm+c＜a﹣b+c，
即am2+bm＜a﹣b，所以D选项正确．
故选：D．
【点评】本题考查了二次函数图象与系数的关系：对于二次函数y＝ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小．当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置．当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右．常数项c决定抛物线与y轴交点位置：抛物线与y轴交于（0，c）．抛物线与x轴交点个数由△决定：Δ＝b2﹣4ac＞0时，抛物线与x轴有2个交点；Δ＝b2﹣4ac＝0时，抛物线与x轴有1个交点；Δ＝b2﹣4ac＜0时，抛物线与x轴没有交点．
8．（2分）使用家用燃气灶烧开同一壶水所需的燃气量y（单位：m3）与旋钮的旋转角度x（单位：度）（0＜x≤90）近似满足函数关系y＝ax2+bx+c（a≠0）．如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为（ ）
A．37.5°B．40°C．42.5°D．45°
【分析】用待定系数法求出解析式，再用二次函数性质即可得到答案．
【解答】解：把（25，0.725），（50，0.06），（60，0.09）代入y＝ax2+bx+c得：
，
解得，
∴y＝0.0001x2﹣0.008x+0.21＝0.0001（x﹣40）2+0.05，
∵0.0001＞0，
∴x＝40时，y最小为0.05，
∴燃气灶烧开一壶水最节省燃气的旋钮角度约为40°，
故选：B．
【点评】本题考查二次函数的应用，解题的关键是掌握待定系数法，求出二次函数解析式．
二、填空题（本题共16分，每小题2分）
9．（2分）请你写出一个二次函数，其图象满足条件：①开口向上；②与y轴的交点坐标为（0，1）．此二次函数的解析式可以是 y＝x2+1 ．
【分析】二次函数的解析式是y＝ax2+bx+c（a、b、c为常数，a≠0），根据开口向上得出a为正数，根据与y轴的交点坐标为（0，1）得出c＝1，写出一个符合的二次函数即可．
【解答】解：答案不唯一，如：y＝x2+1，
故答案为：y＝x2+1．
【点评】本题考查了二次函数的性质，能熟记二次函数的性质内容是解此题的关键．
10．（2分）如图，直线l1∥l2∥l3，直线l4，l5被直线l1、l2、l3所截，截得的线段分别为AB，BC，DE，EF．若AB＝5，BC＝6，EF＝3，则DE的长是 2.5 ．
【分析】根据平行线分线段成比例定理解答即可．
【解答】解：∵直线l1∥l2∥l3，
∴＝，
∵AB＝5，BC＝6，EF＝3，
∴＝，
∴DF＝2.5，
故答案为：2.5．
【点评】本题主要考查了平行线分线段成比例的性质，能够熟练运用其性质是解题的关键．
11．（2分）将二次函数y＝x2+2x﹣1化为y＝（x﹣h）2+k的形式，结果为y＝ y＝（x+1）2﹣2 ．
【分析】利用配方法先提出二次项系数，再加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式．
【解答】解：y＝x2+2x﹣1
＝x2+2x+1﹣1﹣1
＝（x+1）2﹣2．
故答案为：y＝（x+1）2﹣2．
【点评】本题主要考查二次函数的三种形式的知识点，二次函数的解析式有三种形式：
（1）一般式：y＝ax2+bx+c（a≠0，a、b、c为常数）；
（2）顶点式：y＝a（x﹣h）2+k；
（3）交点式（与x轴）：y＝a（x﹣x1）（x﹣x2）．
12．（2分）如图，△AEC中，AE∥BD，CD＝8，DE＝4，那么＝ ．
【分析】由线段的和差关系可得CE的长，再根据相似三角形的判定与性质可得答案．
【解答】解：∵CD＝8，DE＝4，
∴CE＝12，
∵AE∥BD，
∴△CBD∽△CAE，
∴，
故答案为：．
【点评】此题考查的是相似三角形的判定与性质，掌握其性质定理是解决此题的关键．
13．（2分）已知二次函数y＝（x﹣2）2+3，若点A（0，y1）和B（3，y2）在此函数图象上，则y1与y2的大小关系是y1 ＞ y2．（填“＞”，“＜”或“＝”）
【分析】利用二次函数图象上点的坐标特征可求出y1，y2的值，比较后即可得出结论．
【解答】解：∵点A（0，y1）、B（3，y2）是二次函数y＝（x﹣2）2+3图象上的两点，
∴y1＝7，y2＝4．
∴y1＞y2．
故答案为：＞．
【点评】本题考查了二次函数图象上点的坐标特征，利用二次函数图象上点的坐标特征求出y1，y2的值是解题的关键．
14．（2分）已知二次函数y＝ax2+bx+c（a≠0）的部分图象如图所示，则关于x的一元二次方程ax2+bx+c＝0（a≠0）的解为 x1＝6，x2＝﹣2 ．
【分析】抛物线的对称轴为x＝2，抛物线和x轴的一个交点为（6，0），则根据函数的对称性，抛物线和x轴的另外一个交点坐标为（﹣2，0），即可求解．
【解答】解：∵抛物线的对称轴为x＝2，抛物线和x轴的一个交点坐标为（6，0），
则根据函数的对称性，抛物线和x轴的另外一个交点坐标为（﹣2，0），
则关于x的一元二次方程ax2+bx+c＝0（a≠0）的解为x＝6或﹣2，
故答案为：x1＝6，x2＝﹣2．
【点评】本题考查抛物线与x轴的交点坐标，解题的关键是学会利用图象法解决问题，属于中考常考题型．
15．（2分）《九章算术》中记载了一种测量井深的方法．如图所示，在井口B处立一根垂直于井口的木杆BD，从木杆的顶端D观察井水水岸C，视线DC与井口的直径AB交于点E，如果测得AB＝1.8米，BD＝1米，BE＝0.2米，那么AC为 8 米．
【分析】根据平行线的判定定理得到BD∥AC，于是得到△ACE∽△BDE，相似三角形的性质定理即可得到结论．
【解答】解：∵BD⊥AB，AC⊥AB，
∴BD∥AC，
∴△ACE∽△BDE，
∴＝，
∵AB＝1.8米，BD＝1米，BE＝0.2米，
∴AE＝AB﹣BE＝1.6米，
∴＝，
∴AC＝8（米），
故答案为8．
【点评】本题考查了相似三角形的应用，正确的识别图形是解题的关键．
16．（2分）如图，抛物线y＝﹣x2+2．将该抛物线在x轴和x轴上方的部分记作C1，将x轴下方的部分沿x轴翻折后记作C2，C1和C2构成的图形记作C3．
关于图形C3，给出如下四个结论：①图形C3关于y轴成轴对称；②图形C3有最小值，且最小值为0；③当x＞0时，图形C3的函数值都是随着x的增大而增大的；④当﹣2≤x≤2时，图形C3恰好经过5个整点（即横、纵坐标均为整数的点）．以上四个结论中，所有正确结论的序号是 ①②④ ．
【分析】画出翻折后的C2，然后根据图形即可判断．
【解答】解：①由图形可知，图形C3关于y轴成轴对称，故正确；
②图形C3有最小值，且最小值为0，故正确；
③当x＞0时，图形C3的函数值先随着x的增大而减小，当函数值为0后，再随x的增大而增大，故③错误；
④当﹣2≤x≤2时，图形C3恰好经过（﹣2，2），（﹣1，1），（0，2），（1，1），（2，2）共5个整点（即横、纵坐标均为整数的点），故④正确，
所以，①②④是正确的结论．
故答案为：①②④．
【点评】本题考查了二次函数的图象与几何变换，数形结合是解题的关键．
三、解答题（本题共12道小题，第17-22题，每小题5分，第23-26题，每小题5分，第27，28题，每小题5分，共68分）
17．（5分）已知二次函数y＝x2﹣4．
（1）求该二次函数图象的对称轴与顶点坐标；
（2）求该二次函数图象与x轴、y轴的交点．
【分析】（1）由二次函数顶点式求解．
（2）分别将x＝0，y＝0代入解析式求解．
【解答】解：（1）∵y＝x2﹣4，
∴抛物线开口向上，对称轴为y轴，顶点坐标为（0，﹣4）．
（2）将y＝0代入y＝x2﹣4得0＝x2﹣4，
解得x1＝﹣2，x2＝2，
抛物线与x轴交点坐标为（﹣2，0），（2，0），
将x＝0代入y＝x2﹣4得y＝﹣4，
∴抛物线与y轴交点坐标为（0，﹣4）．
【点评】本题考查二次函数的性质，解题关键是掌握二次函数图象与系数的关系．
18．（5分）如图，在△ABC中，∠C＝90°，点D是AC上一点，DE⊥AB于点E．求证：△ABC∽△ADE．
【分析】根据相似三角形的判定即可求出答案．
【解答】证明：∵DE⊥AB于点E，
∴∠AED＝∠C＝90°．
∵∠A＝∠A，
∴△ABC∽△ADE．
【点评】本题考查相似三角形，解题的关键是熟练运用相似三角形判定，本题属于中等题型．
19．（5分）如图，函数y＝﹣x2+bx+c的图象经过点A，B，C．求此函数表达式．
【分析】把A、B的坐标代入y＝﹣x2+bx+c，求得b、c的值，利用待定系数法即可求得函数的表达式．
【解答】解：∵函数y＝﹣x2+bx+c的图象经过点A，B，C，A（﹣1，0），B（0，3），
∴，解得，
∴此函数表达式为y＝﹣x2+2x+3．
【点评】本题考查了待定系数法求二次函数的解析式，熟练掌握待定系数法是解题的关键．
20．（5分）如图是边长为1的正方形网格，△A1B1C1的顶点均在格点上．
（1）在该网格中画出△A2B2C2（△A2B2C2的顶点均在格点上），使△A2B2C2∽△A1B1C1；
（2）说明△A2B2C2和△A1B1C1相似的依据．
【分析】（1）利用相似三角形的判定画出图形即可；
（2）根据三边成比例两三角形相似判断即可．
【解答】解：（1）如图，△A2B2C2即为所求；
（2）相似的理由是三边成比例两三角形相似．
【点评】本题考查作图﹣相似变换，解题的关键是掌握相似变换的性质，属于中考常考题型．
21．（5分）一个二次函数图象上部分点的横坐标x，纵坐标y的对应值如下表：
（1）求这个二次函数的表达式；
（2）求m的值；
（3）在给定的直角坐标系中，画出这个函数的图象；
（4）根据图象，写出当y＜0时，x的取值范围．
【分析】（1）先确定出顶点坐标，再设顶点式解析式为y＝a（x+1）2+2，然后将点（1，0）代入求出a的值，从而得解；
（2）将x＝2代入函数解析式计算即可得解；
（3）根据二次函数图象的画法作出图象即可；
（4）根据函数图象，写出x轴上方部分的x的取值范围即可．
【解答】解：（1）由图表可知抛物线的顶点坐标为（﹣1，2），
所以，设这个二次函数的表达式为y＝a（x+1）2+2，
∵图象过点（1，0），
∴a（1+1）2+2＝0，
∴a＝﹣，
∴这个二次函数的表达式为y＝﹣（x+1）2+2；
（2）x＝2时，m＝﹣（2+1）2+2＝﹣；
（3）函数图象如图所示；
（4）y＜0时，x＜﹣3或x＞1．
【点评】本题考查了抛物线与x轴的交点问题，二次函数的性质，待定系数法求二次函数解析式，读懂题目信息，从表格中判断出顶点坐标是解题的关键．
22．（5分）已知：如图，在Rt△ABC中，∠ACB＝90°，CD是AB边上的高．
（1）求证：△ABC∽△CBD；
（2）如果AD＝4，BD＝3，求BC的长．
【分析】（1）由于∠ACB＝∠CDB＝90°，∠B＝∠B，从而可证明△ABC∽△CBD；
（2）根据已知可求出AB＝7，根据相似三角形的性质，从而可求出BD的长度．
【解答】（1）证明：∵∠ACB＝90°，CD 是AB 边上的高，
∴∠ACB＝∠CDB＝90°，
又∵∠B＝∠B，
∴△ABC∽△CBD；
（2）解：∵AD＝4，BD＝3，
∴AB＝7，
∵△ABC∽△CBD，
∴，
∴BC＝．
【点评】本题考查相似三角形的综合问题，解题的关键是熟练运用相似三角形的性质与判定，本题属于中等题型．
23．（6分）如图，在平行四边形ABCD中，点E在BC边上，点F在DC的延长线上，且∠AEB＝∠F．
（1）求证：△ABE∽△ECF；
（2）若AB＝5，CE＝6，BE＝2，求FD的长．
【分析】（1）根据平行四边形的性质得出AB∥CD 故∠ABE＝∠ECF，再由∠AEB＝∠F即可得出结论；
（2）根据相似三角形的对应边成比例即可得出结论．
【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠ABE＝∠ECF．
∵∠AEB＝∠F，
∴△ABE∽△ECF．
（2）解：∵△ABE∽△ECF，
∴，
∴，
∴CF＝，
∴DF＝DC+CF＝AB+CF＝5+＝．
【点评】本题考查的是相似三角形的判定与性质，熟知相似三角形的对应边成比例是解答此题的关键．
24．（6分）2022年北京冬奥会即将召开，激起了人们对冰雪运动的极大热情．如图是某跳台滑雪训练场的横截面示意图，取某一位置的水平线为x轴，过跳台终点A作水平线的垂线为y轴，建立平面直角坐标系．图中的抛物线C1：y＝﹣x+1近似表示滑雪场地上的一座小山坡，某运动员从点O正上方4米处的A点滑出，滑出后沿一段抛物线C2：y＝﹣+bx+c运动．
（1）当运动员运动到离A处的水平距离为4米时，离水平线的高度为8米，求抛物线C2的函数解析式（不要求写出自变量x的取值范围）；
（2）在（1）的条件下，当运动员运动水平线的水平距离为多少米时，运动员与小山坡的竖直距离为1米？
【分析】（1）根据题意将点（0，4）和（4，8）代入C2：y＝﹣x2+bx+c求出b、c的值即可写出C2的函数解析式；
（2）设运动员运动的水平距离为m米时，运动员与小山坡的竖直距离为1米，依题意得：﹣m2+m+4﹣（﹣m2+m+1）＝1，解出m即可．
【解答】解：（1）由题意可知抛物线C2：y＝﹣x2+bx+c过点（0，4）和（4，8），将其代入得：
，
解得：，
∴抛物线C2的函数解析式为：y＝﹣x2+x+4；
（2）设运动员运动的水平距离为m米时，运动员与小山坡的竖直距离为1米，依题意得：
﹣m2+m+4﹣（﹣m2+m+1）＝1，
整理得：（m﹣12）（m+4）＝0，
解得：m1＝12，m2＝﹣4（舍去），
故运动员运动的水平距离为12米时，运动员与小山坡的竖直距离为1米．
【点评】本题考查二次函数的基本性质及其应用，熟练掌握二次函数的基本性质，并能将实际问题与二次函数模型相结合是解决本题的关键．
25．（6分）学习完《相似形》一章之后，数学兴趣小组利用相似三角形的有关知识测量校园内一棵树高，他们的方法如下：
如图，为了测量操场上一棵大树的高度，小英拿来一面镜子，平放在离树根部5m的地面上，然后她沿着树根和镜子所在的直线后退，当她后退1m时，正好在镜中看见树的顶端．小英估计自己的眼睛到地面的距离为1.6m，则可测得大树的高度．
（1）请你根据上述方法求出树高；
（2）请你设计一个其他的测量方案，并简述方案．
【分析】（1）入射角等于反射角，两个直角相等，那么图中的两个三角形相似，利用对应边成比例可求得树高；
（2）在距离树AB的a米的C处，用测角仪测得仰角α，测角仪为CD．再根据仰角的定义，构造直角三角形ADE，利用三角函数计算可得答案．
【解答】解：（1）∵∠ABC＝∠DBE，∠ACB＝∠DEB＝90°，
∴△ABC∽△DBE，
∴BC：BE＝AC：DE，
即1：5＝1.6：DE，
∴DE＝8m，
∴大树的高度为8m；
（2）在距离树AB的a米的C处，用测角仪测得仰角α，测角仪为CD．
再根据仰角的定义，构造直角三角形ADE，求得树高出测角仪的高度AE，则树高为AE+BE．
【点评】本题考查相似三角形性质的应用．解题时关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题．
26．（6分）在平面直角坐标系xOy中，已知抛物线y＝ax2﹣2ax+4（a＞0）．
（1）求该抛物线的对称轴和顶点坐标（用含a的代数式表示）；
（2）如果该抛物线的顶点恰好在x轴上，求它的表达式；
（3）如果A（m﹣1，y1），B（m，y2），C（m+2，y3）三点均在抛物线y＝ax2﹣2ax+4上，且总有y1＞y3＞y2，结合图象，直接写出m的取值范围．
【分析】（1）解析式化成顶点式即可求得对称轴和顶点坐标；
（2）根据题意Δ＝（﹣2a）2﹣4a×4＝0，解得a＝4，即可得到抛物线的表达式为y＝4x2﹣8x+4；
（3）根据题意得到，解不等式组即可．
【解答】解：（1）∵y＝ax2﹣2ax+4＝a（x﹣1）2﹣a+4，
∴该抛物线的对称轴为直线x＝1，顶点坐标为（1，4﹣a）；
（2）∵抛物线的顶点恰好在x轴上，
∴方程ax2﹣2ax+4＝0有两个相等的根，
∴Δ＝（﹣2a）2﹣4a×4＝0，
解得a＝4或a＝0（不符合题意，舍去），
∴抛物线的表达式为y＝4x2﹣8x+4；
（3）∵a＞0，
∴抛物线开口向上，
∵A（m﹣1，y1）、B（m，y2）、C（m+2，y3）为该抛物线上三点，且总有y1＞y3＞y2，抛物线的对称轴为直线x＝1，
∴，
解得0＜m＜．
∴m的取值范围是0＜m＜．
【点评】本题考查了待定系数法求二次函数的解析式，二次函数图象上点的坐标特征，二次函数的性质，熟练掌握二次函数的性质是解题的关键．
27．（7分）如图，O为四边形ABCD内一点，E为AB的中点，OA＝OD，OB＝OC，∠AOB+∠COD＝180°．
（1）若∠BOE＝∠BAO，AB＝，求OB的长；
（2）用等式表示线段OE和CD之间的关系，并证明．
【分析】（1）通过证明△OBE∽△ABO，可得，即可求解；
（2）如图，延长OE到点F，使得EF＝OF，连接AF，FB，可证四边形AFBO是平行四边形，可得AF∥OB，AF＝OB，由“SAS”可证△AOF≌△DOC，可得OF＝CD，可得结论．
【解答】（1）解：∵∠BOE＝∠BAO，∠OBE＝∠ABO，
∴△OBE∽△ABO，
∴，
∵AB＝2，E为AB的中点，
∴BE＝，
∴，
∴OB＝2，OB＝﹣2（不合题意舍去），
∴OB＝2；
（2）解：线段OE和CD的数量关系是OE＝CD，理由如下：
如图，延长OE到点F，使得EF＝EO，连接AF，FB，
∵AE＝BE，OE＝EF，
∴四边形AFBO是平行四边形，
∴AF∥OB，AF＝OB，
∴∠FAO+∠AOB＝180°，
∵∠AOB+∠COD＝180°，
∴∠FAO＝∠COD，
∵OB＝OC，
∴AF＝OC，
在△AOF和△ODC中，
，
∴△AOF≌△ODC（SAS），
∴OF＝CD，
∴OE＝CD．
【点评】本题考查了全等三角形的判定和性质，相似三角形的判定和性质，平行四边形的判定和性质等知识，灵活运用这些性质解决问题是解题的关键．
28．（7分）对某一个函数给出如下定义：如果存在实数M，对于任意的函数值y，都满足y≤M，那么称这个函数是有上界函数．在所有满足条件的M中，其最小值称为这个函数的上确界．例如，图中的函数y＝﹣（x﹣3）2+2是有上界函数，其上确界是2．
（1）函数①y＝x2+2x+1和②y＝2x﹣3（x≤2）中是有上界函数的为 ② （只填序号即可），其上确界为 1 ；
（2）如果函数y＝﹣x+2（a≤x≤b，b＞a）的上确界是b，且这个函数的最小值不超过2a+1，求a的取值范围；
（3）如果函数y＝x2﹣2ax+2（1≤x≤5）是以3为上确界的有上界函数，求实数a的值．
【分析】（1）分别求出两个函数的最大值即可求解；
（2）由题意可知：﹣b+2≤y≤﹣a+2，再由﹣a+2＝b，﹣b+2≤2a+1，b＞a，即可求a的取值范围；
（3）当a≤1时，27﹣10a＝3，可得a＝2.4（舍）；当a≥5时，3﹣2a＝3，可得a＝0（舍）；当1＜a≤3时，27﹣10a＝3，可得a＝2.4；当3＜a＜5时，3﹣2a＝3，可得a＝0．
【解答】解：（1）①y＝x2+2x+1＝（x+1）2≥0，
∴①无上确界；
②y＝2x﹣3（x≤2），
∴y≤1，
∴②有上确界，且上确界为1，
故答案为：②，1；
（2）∵y＝﹣x+2，y随x值的增大而减小，
∴当a≤x≤b时，﹣b+2≤y≤﹣a+2，
∵上确界是b，
∴﹣a+2＝b，
∵函数的最小值不超过2a+1，
∴﹣b+2≤2a+1，
∴a≥﹣1，
∵b＞a，
∴﹣a+2＞a，
∴a＜1，
∴a的取值范围为：﹣1≤a＜1；
（3）y＝x2﹣2ax+2的对称轴为直线x＝a，
当a≤1时，y的最大值为25﹣10a+2＝27﹣10a，
∵3为上确界，
∴27﹣10a＝3，
∴a＝2.4（舍）；
当a≥5时，y的最大值为1﹣2a+2＝3﹣2a，
∵3为上确界，
∴3﹣2a＝3，
∴a＝0（舍）；
当1＜a≤3时，y的最大值为25﹣10a+2＝27﹣10a，
∵3为上确界，
∴27﹣10a＝3，
∴a＝2.4；
当3＜a＜5时，y的最大值为1﹣2a+2＝3﹣2a，
∵3为上确界，
∴3﹣2a＝3，
∴a＝0，
综上所述：a的值为2.4．
【点评】本题是二次函数的综合题，熟练掌握二次函数的图象及性质，根据所给范围分类讨论求二次函数的最大值是解题的关键．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2023/7/11 11:48:19；用户：笑涵数学；邮箱：15699920825；学号：36906111x
…
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
…
y
…
﹣
0
2
0
m
﹣6
﹣
…
x
…
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
…
y
…
﹣
0
2
0
m
﹣6
﹣
…