2022-2023学年北京市大兴区八年级（上）期中数学试卷【含解析】

这是一份2022-2023学年北京市大兴区八年级（上）期中数学试卷【含解析】，共30页。试卷主要包含了填空题，解答题解答应写出文字说明等内容，欢迎下载使用。
1．（2分）在美术字中，有些汉字是轴对称的．下列美术字是轴对称的是（ ）
A．爱B．我C．中D．国
2．（2分）下列长度的三条线段，能组成三角形的是（ ）
A．8，6，5B．3，4，8C．4，6，10D．3，3，6
3．（2分）五边形的内角和为（ ）
A．360°B．540°C．720°D．900°
4．（2分）如图图形中，作△ABC的边BC上的高，正确的是（ ）
A．B．
C．D．
5．（2分）如图，AB∥DE，点B，C，D在同一直线上，若∠BCE＝55°，∠E＝25°，则∠B的度数是（ ）
A．55°B．30°C．25°D．20°
6．（2分）如图，△ABC≌△A'B′C'，若∠A＝36°，∠C＝24°，则∠B′的度数是（ ）
A．60°B．90°C．100°D．120°
7．（2分）若从n边形的一个顶点出发，可以画出4条对角线，则n的值是（ ）
A．4B．5C．6D．7
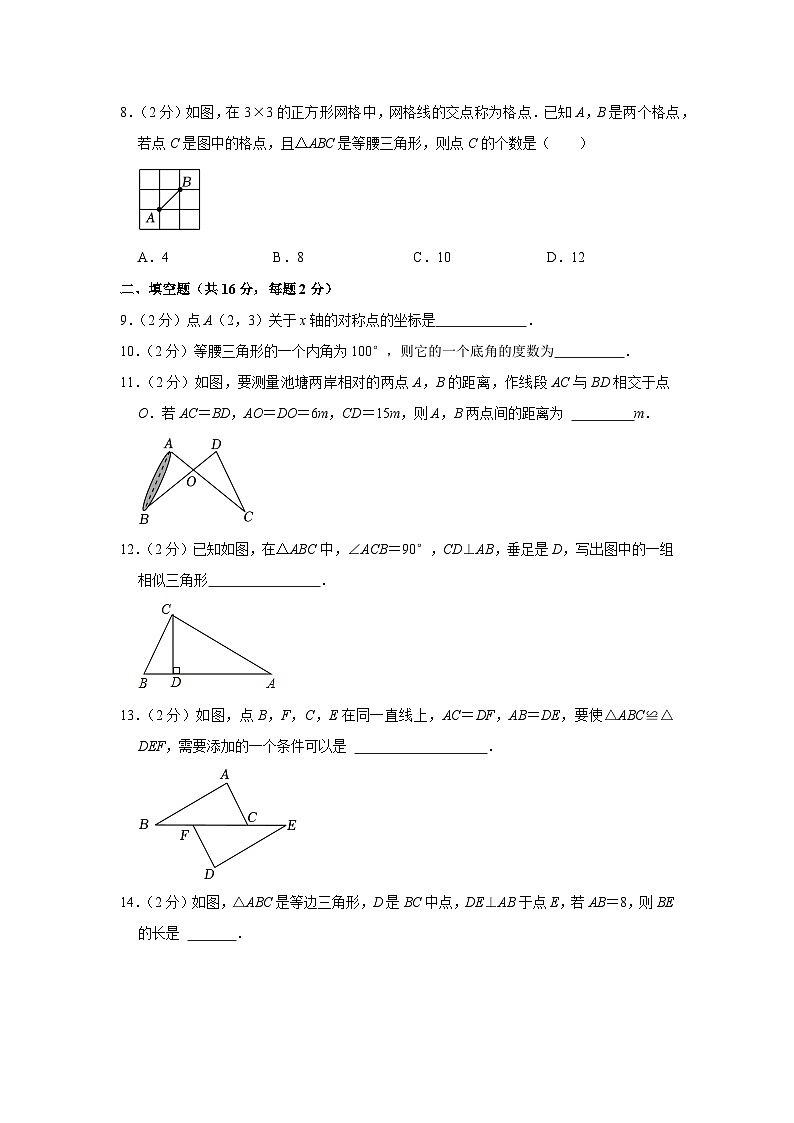
8．（2分）如图，在3×3的正方形网格中，网格线的交点称为格点．已知A，B是两个格点，若点C是图中的格点，且△ABC是等腰三角形，则点C的个数是（ ）
A．4B．8C．10D．12
二、填空题（共16分，每题2分）
9．（2分）点A（2，3）关于x轴的对称点的坐标是 ．
10．（2分）等腰三角形的一个内角为100°，则它的一个底角的度数为 ．
11．（2分）如图，要测量池塘两岸相对的两点A，B的距离，作线段AC与BD相交于点O．若AC＝BD，AO＝DO＝6m，CD＝15m，则A，B两点间的距离为 m．
12．（2分）已知如图，在△ABC中，∠ACB＝90°，CD⊥AB，垂足是D，写出图中的一组相似三角形 ．
13．（2分）如图，点B，F，C，E在同一直线上，AC＝DF，AB＝DE，要使△ABC≌△DEF，需要添加的一个条件可以是 ．
14．（2分）如图，△ABC是等边三角形，D是BC中点，DE⊥AB于点E，若AB＝8，则BE的长是 ．
15．（2分）将图1中的△ABC折叠，使点A与点C重合，折痕为ED，点E，D分别在AB，AC上，得到图形2．若BC＝4，AB＝5，则△EBC的周长是 ．
16．（2分）如图，△ABC与△ADE都是等边三角形，BD和CE相交于点P，连接AP．下面结论中，①BD＝CE；②∠EPD＝60°；③PA不是∠BPE的平分线；④PE＝PA+PD．所有正确结论的序号是 ．
三、解答题（共68分，第17-24题，每题5分，第25题6分，第26，27题，每题7分，第28题8分）解答应写出文字说明、演算步骤或证明过程.
17．（5分）用一条长20cm的细绳围成一个等腰三角形，若一腰长是底边长的2倍，求各边的长．
18．（5分）一个多边形的内角和是它外角和的2倍，求这个多边形的边数．
19．（5分）如图，点A，B，C，D在同一直线上，AE＝BF，EC＝FD，AB＝CD．
求证：△EAC≌△FBD．
20．（5分）如图，线段AC与线段BD相交于点O，若∠A＝70°，∠B＝30°，∠C＝60°，求∠D的度数．
21．（5分）如图，线段AC与线段BD相交于点E，∠A＝∠D，AE＝DE．
求证：BD＝AC．
22．（5分）如图，AB，CD相交于点O，DE∥AB．
（1）作∠BOD的角平分线OM，交DE于点F（要求：尺规作图，保留作图痕迹，不写作法）；
（2）若∠D＝60°，则△ODF的形状是 ．
23．（5分）如图，为了满足A，B，C三个小区居民的体育锻炼需求，需要建立一个居民健身广场D，要使健身广场到三个小区的距离相等，请你在图中作出健身广场D的位置（要求：尺规作图，保留作图痕迹，不写作法）．
24．（5分）如图1，AD是△ABC的中线．
求证：AB+AC＞2AD．
请将下面的推理过程补充完整：
证明：如图2，延长AD到点E，使DE＝AD，连接BE．
∵AD是△ABC的中线，
∴BD＝CD．
在△ADC和△EDB中，
∴△ADC≌△EDB （ ）．
∴ （全等三角形的对应边相等）．
∴在△ABE中，AB+BE＞AE （ ），
∴AB+AC＞AD+DE．
即AB+AC＞2AD．
25．（6分）如图，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E，F，BE＝CF．求证：AD是△ABC的角平分线．
26．（7分）在四边形ABCD中，∠A+∠C＝180°，BD平分∠ABC．
（1）如图1，若∠A＝90°．
①直接写出AD与CD的数量关系： ；
②请你写出图中一个与①不同的正确结论： ；
（2）如图2，若∠A＞90°，猜想AD与CD的数量关系，并证明．
27．（7分）如图，在等边△ABC中，点D是BC边上一点，作射线AD，点B关于射线AD的对称点为E，连接CE并延长交射线AD于点F．
（1）依题意补全图形；
（2）若∠BAF＝10°，则∠EFA的度数是 ；
（3）用等式表示线段AF，CF，EF之间的数量关系，并证明．
28．（8分）在平面直角坐标系xOy中，点A，B，P不在同一直线上，对于点P和线段AB给出如下定义：过点P向线段AB所在直线作垂线，若垂足Q在线段AB上，则称点P为线段AB的内垂点，当垂足Q满足|AQ﹣BQ|最小时，称点P为线段AB的最佳内垂点．
已知点S（﹣3，1），T（1，1）．
（1）在点P1（2，4），P2（﹣4，0），P3（﹣2，），P4（1，3）中，线段ST的内垂点为 ；
（2）若点M是线段ST的最佳内垂点，则点M的坐标可以是 （写出两个满足条件的点M即可）；
（3）已知点C（m﹣2，3），D（m，3），若线段CD上的每一个点都是线段ST的内垂点，直接写出m的取值范围；
（4）已知点E（n+2，0），F（n+4，﹣1），若线段EF上存在线段ST的最佳内垂点，直接写出n的取值范围．
2022-2023学年北京市大兴区八年级（上）期中数学试卷
参考答案与试题解析
一、选择题（共16分，每题2分）第1-8题均有四个选项，符合题意的选项只有一个.
1．（2分）在美术字中，有些汉字是轴对称的．下列美术字是轴对称的是（ ）
A．爱B．我C．中D．国
【分析】根据轴对称的概念得出结论即可．
【解答】解：由题意知，“中”字是轴对称的，
故选：C．
【点评】本题主要考查轴对称的知识，熟练掌握轴对称的知识是解题的关键．
2．（2分）下列长度的三条线段，能组成三角形的是（ ）
A．8，6，5B．3，4，8C．4，6，10D．3，3，6
【分析】根据三角形的三条边必须满足任意两边之和大于第三边，任意两边之差小于第三边即可判断．
【解答】解：A、6+5＞8，能组成三角形，符合题意；
B、3+4＜8，不能组成三角形，不符合题意．
C、4+6＝10，不能组成三角形，不符合题意；
D、3+3＝6，不能组成三角形，不符合题意；
故选：A．
【点评】本题主要考查对三角形三边关系的理解应用．判断是否可以构成三角形，只要判断两个较小的数的和大于最大的数即可．
3．（2分）五边形的内角和为（ ）
A．360°B．540°C．720°D．900°
【分析】n边形的内角和是（n﹣2）180°，由此即可求出答案．
【解答】解：五边形的内角和是（5﹣2）×180°＝540°．故选：B．
【点评】本题主要考查了多边形的内角和公式，是需要熟记的内容．
4．（2分）如图图形中，作△ABC的边BC上的高，正确的是（ ）
A．B．
C．D．
【分析】根据三角形的高的概念判断即可．
【解答】解：A、图形中，AD是△ABC的BC边上的高，本选项符合题意；
B、图形中，不能表示△ABC的BC边上的高，本选项不符合题意；
C、图形中，不能表示△ABC的BC边上的高，本选项不符合题意；
D、图形中，不能表示△ABC的BC边上的高，本选项不符合题意；
故选：A．
【点评】本题考查的是三角形的高的概念，从三角形的一个顶点向对边作垂线，垂足与顶点之间的线段叫做三角形的高．
5．（2分）如图，AB∥DE，点B，C，D在同一直线上，若∠BCE＝55°，∠E＝25°，则∠B的度数是（ ）
A．55°B．30°C．25°D．20°
【分析】根据三角形外角和内角的关系，可以得到∠D的度数，再根据平行线的性质，可以得到∠D＝∠B，从而可以得到∠B的度数．
【解答】解：∵∠BCE＝55°，∠E＝25°，∠BCE＝∠E+∠D，
∴∠D＝∠BCE﹣∠E＝55°﹣25°＝30°，
∵AB∥DE，
∴∠B＝∠D，
∴∠B＝30°，
故选：B．
【点评】本题考查平行线的性质、三角形外角和内角的关系，解答本题的关键是求出∠D的度数．
6．（2分）如图，△ABC≌△A'B′C'，若∠A＝36°，∠C＝24°，则∠B′的度数是（ ）
A．60°B．90°C．100°D．120°
【分析】根据全等三角形的性质求出∠A′＝36°，∠C′＝24°，，再根据三角形内角和定理计算，得到答案．
【解答】解：∵△ABC≌△A'B'C'，∠A＝36°，∠C＝24°，
∴∠A′＝∠A＝36°，∠C′＝∠C＝24°，
∴∠B′＝180°﹣∠A′﹣∠C′＝180°﹣36°﹣24°＝120°，
故选：D．
【点评】本题考查的是全等三角形的性质、三角形内角和定理，掌握全等三角形的对应角相等是解题的关键．
7．（2分）若从n边形的一个顶点出发，可以画出4条对角线，则n的值是（ ）
A．4B．5C．6D．7
【分析】根据n边形从一个顶点出发可引出（n﹣3）条对角线，可得n﹣3＝5，求出n的值．
【解答】解：设多边形有n条边，
则n﹣3＝4，
解得n＝7，
故选：D．
【点评】本题考查了多边形的对角线，熟记n边形从一个顶点出发可引出（n﹣3）条对角线是解答此题的关键．
8．（2分）如图，在3×3的正方形网格中，网格线的交点称为格点．已知A，B是两个格点，若点C是图中的格点，且△ABC是等腰三角形，则点C的个数是（ ）
A．4B．8C．10D．12
【分析】根据题意，结合图形，分两种情况讨论：①AB为等腰△ABC底边；②AB为等腰△ABC其中的一条腰．
【解答】解：如图：分情况讨论．
①AB为等腰△ABC底边时，符合条件的C点有4个；
②AB为等腰△ABC其中的一条腰时，符合条件的C点有4个．
故选：B．
【点评】此题主要考查了等腰三角形的判定，解答本题关键是根据题意，画出符合实际条件的图形，再利用分类讨论思想解答．
二、填空题（共16分，每题2分）
9．（2分）点A（2，3）关于x轴的对称点的坐标是 （2，﹣3） ．
【分析】根据“关于x轴对称的点，横坐标相同，纵坐标互为相反数”解答．
【解答】解：点A（2，3）关于x轴的对称点的坐标是（2，﹣3）．
故答案为：（2，﹣3）．
【点评】本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：
（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；
（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数；
（3）关于原点对称的点，横坐标与纵坐标都互为相反数．
10．（2分）等腰三角形的一个内角为100°，则它的一个底角的度数为 40° ．
【分析】由于等腰三角形的一个内角为100°，这个角是顶角或底角不能确定，故应分两种情况进行讨论．
【解答】解：①当这个角是顶角时，底角＝（180°﹣100°）÷2＝40°；
②当这个角是底角时，另一个底角为100°，因为100°+100°＝200°，不符合三角形内角和定理，所以舍去．
故答案为：40°．
【点评】本题考查的是等腰三角形的性质，解答此类问题时往往用到三角形的内角和是180°这一隐藏条件．
11．（2分）如图，要测量池塘两岸相对的两点A，B的距离，作线段AC与BD相交于点O．若AC＝BD，AO＝DO＝6m，CD＝15m，则A，B两点间的距离为 15 m．
【分析】结合AC＝BD，AO＝DO，可得BO＝CO，再利用∠AOB＝∠DOC，即可证出△ABO≌△DCO（SAS），利用全等三角形的性质可得出AB＝CD．
【解答】解：∵AC＝BD，AO＝DO＝6m，
∴BO＝CO，
在△ABO和△DCO中，
，
∴ABO≌△DCO（SAS），
∴AB＝DC＝15m．
故答案为：15．
【点评】本题考查了全等三角形的应用，利用全等三角形的判定定理SAS证出△ABO≌△DCO是解题的关键．
12．（2分）已知如图，在△ABC中，∠ACB＝90°，CD⊥AB，垂足是D，写出图中的一组相似三角形 △ABC∽△ACD ．
【分析】由题意及图形可知：此图中共有3个直角三角形，根据相似三角形的判定和性质判断即可．
【解答】解：①在Rt△ABC中，∠ACB＝90°，CD⊥AB，
∴∠BDC＝90°，∠ADC＝90°，
在Rt△ADC和Rt△ACB中，∠A＝∠A，∠C＝∠ADC，
∴Rt△ADC∽Rt△ACB；
②在Rt△ADC和Rt△BCD中，∵∠BDC＝∠ADC＝90°，
又∵∠ACD+∠BCD＝90°，∠BCD+∠B＝90°，
∴∠ACD＝∠B，
∴Rt△ADC∽Rt△BCD；
③在Rt△ABC和Rt△BCD中，∠C＝∠BDC＝90°，∠B＝∠B，
∴Rt△ABC∽Rt△BCD．
故答案是：△ABC∽△ACD．
【点评】本题考查了相似三角形的判定定理，此题只要运用了：“如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似，”（简叙为两角对应相等两三角形相似）这一定理．
13．（2分）如图，点B，F，C，E在同一直线上，AC＝DF，AB＝DE，要使△ABC≌△DEF，需要添加的一个条件可以是 ∠A＝∠D（答案不唯一） ．
【分析】根据题意可知，两个三角形满足两边对应相等，根据“SAS”可添加∠A＝∠D或根据“SSS”可添加BC＝EF或BF＝CE，能够使△ABC≌△DEF．
【解答】解：∠A＝∠D．
理由是：在△ABC和△DEF中，
，
∴△ABC≌△DEF（SAS），
故答案为：∠A＝∠D（答案不唯一）．
【点评】本题考查了全等三角形的判定：全等三角形的5种判定方法中，选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组边对应相等，这条边可以是两角的夹边，也可以是其中一个角的对边；若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．
14．（2分）如图，△ABC是等边三角形，D是BC中点，DE⊥AB于点E，若AB＝8，则BE的长是 2 ．
【分析】连接AD，利用等边三角形的性质可得∠B＝∠BAC＝60°，AB＝AC，从而利用等腰三角形的三线合一性质可得∠BAD＝30°，∠ADB＝90°，然后在Rt△ADB中，利用含30度角的直角三角形的性质可得BD＝AB＝4，再根据垂直定义可得∠DEB＝90°，从而利用直角三角形的两个锐角互余可得∠BDE＝30°，最后在Rt△BDE中，利用含30度角的直角三角形的性质可得BE＝BD＝2，即可解答．
【解答】解：连接AD，
∵△ABC是等边三角形，
∴∠B＝∠BAC＝60°，AB＝AC，
∵AB＝AC，D是BC中点，
∴∠BAD＝∠BAC＝30°，∠ADB＝90°，
∴BD＝AB＝4，
∵DE⊥AB，
∴∠DEB＝90°，
∴∠BDE＝90°﹣∠B＝30°，
∴BE＝BD＝2，
故答案为：2．
【点评】本题考查了等边三角形的性质，含30度角的直角三角形的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
15．（2分）将图1中的△ABC折叠，使点A与点C重合，折痕为ED，点E，D分别在AB，AC上，得到图形2．若BC＝4，AB＝5，则△EBC的周长是 9 ．
【分析】由折叠的性质可得出AE＝CE，则可得出△EBC的周长＝AB+CB，可求出答案．
【解答】解：∵将图1中的△ABC折叠，使点A与点C重合，
∴AE＝CE，
∴△EBC的周长＝BE+CE+BC
＝BE+AE+BC
＝AB+BC
＝5+4
＝9．
故答案为：9．
【点评】本题考查了折叠的性质，三角形的周长，熟练掌握折叠的性质是解题的关键．
16．（2分）如图，△ABC与△ADE都是等边三角形，BD和CE相交于点P，连接AP．下面结论中，①BD＝CE；②∠EPD＝60°；③PA不是∠BPE的平分线；④PE＝PA+PD．所有正确结论的序号是 ①②④ ．
【分析】由“SAS”可证△BAD≌△CAE，可得BD＝CE；由全等三角形的性质可得∠ABD＝∠ACE，由外角的性质和三角形内角和定理可得∠EPD＝60°；由全等三角形的性质可得S△BAD＝S△CAE，由三角形面积公式可得AH＝AF，由角平分线的性质可得AP平分∠BPE；由全等三角形的性质可得∠BDA＝∠CEA，由“SAS”可证△AOE≌△APD，由全等三角形的性质得出AO＝AP，证明△APO是等边三角形，可得AP＝PO，可得PE＝AP+PD，即可求解．
【解答】解：∵△ABC与△ADE都是等边三角形，
∴∠BAC＝∠DAE＝60°，
∴∠BAD＝∠CAE，AB＝AC，AD＝AE，
∴△BAD≌△CAE（SAS），
∴BD＝CE，故①正确，
∵△BAD≌△CAE，
∴∠AEC＝∠ADB，
∵∠ANE＝∠DNP，
∴∠DPE＝∠DAE＝60°，故②正确；
如图，过点A作AH⊥BD，AF⊥CE，
∵△BAD≌△CAE，
∴S△BAD＝S△CAE，
∴BD•AH＝CE•AF，
∵BD＝CE，
∴AH＝AF，
∵AH⊥BD，AF⊥CE，
∴AP平分∠BPE，故③错误；
如图，在线段PE上截取OE＝PD，连接AO，
∵△BAD≌△CAE，
∴∠BDA＝∠CEA，
∵OE＝PD，AE＝AD，
∴△AOE≌△APD（SAS），
∴AP＝AO，∠PAD＝∠OAE，
∴∠PAO＝∠DAE＝60°，
∴△APO是等边三角形，
∴AP＝PO，
∵PE＝PO+OE，
∴PE＝AP+PD，故④正确．
故答案为：①②④．
【点评】本题主要考查了全等三角形的判定和性质，直角三角形的性质，等边三角形的判定和性质以及角之间的关系，证明△BAD≌△CAE是解本题的关键．
三、解答题（共68分，第17-24题，每题5分，第25题6分，第26，27题，每题7分，第28题8分）解答应写出文字说明、演算步骤或证明过程.
17．（5分）用一条长20cm的细绳围成一个等腰三角形，若一腰长是底边长的2倍，求各边的长．
【分析】设底长为xcm，则腰边长为 2xcm，根据周长列方程得到x+2x+2x＝20，然后解方程求出x，从而得到三角形的底边与腰长．
【解答】解：设底长为xcm，则腰边长为 2xcm，
根据题意得x+2x+2x＝20，
解得x＝4，
当x＝4时，2x＝8，
所以三角形的腰长为8cm、8cm，底边长为4cm；
【点评】本题考查了等腰三角形的判定：如果一个三角形有两个角相等，那么这两个角所对的边也相等．也考查了三角形三边的关系．
18．（5分）一个多边形的内角和是它外角和的2倍，求这个多边形的边数．
【分析】根据多边形的内角和公式（n﹣2）•180°以及外角和定理列出方程，然后求解即可．
【解答】解：设这个多边形的边数是n，
根据题意得，（n﹣2）•180°＝2×360°，
解得n＝6．
答：这个多边形的边数是6．
【点评】本题考查了多边形的内角和公式与外角和定理，需要注意，多边形的外角和与边数无关，任何多边形的外角和都是360°．
19．（5分）如图，点A，B，C，D在同一直线上，AE＝BF，EC＝FD，AB＝CD．
求证：△EAC≌△FBD．
【分析】根据线段的和差求出AC＝BD，利用SSS即可证明△EAC≌△FBD．
【解答】证明：∵AB＝CD，
∴AB+BC＝CD+BC，
即AC＝BD，
在△EAC和△FBD中，
，
∴△EAC≌△FBD（SSS）．
【点评】此题考查了全等三角形的判定，熟记全等三角形的判定定理是解题的关键．
20．（5分）如图，线段AC与线段BD相交于点O，若∠A＝70°，∠B＝30°，∠C＝60°，求∠D的度数．
【分析】先根据8字形和三角形内角和定理可解答．
【解答】解：∵∠AOB＝∠COD，
∴∠A+∠B＝∠C+∠D，
∵∠A＝70°，∠B＝30°，∠C＝60°，
∴70°+30°＝60°+∠D，
∴∠D＝40°．
【点评】本题考查了三角形的内角和定理，掌握8字形内角的关系是解题的关键．
21．（5分）如图，线段AC与线段BD相交于点E，∠A＝∠D，AE＝DE．
求证：BD＝AC．
【分析】先由∠A＝∠D，AE＝DE，∠AEB＝∠DEC，根据全等三角形的判定定理“ASA”证明△ABE≌△DCE，得BE＝CE，再根据等式的性质得DE+BE＝AE+CE，所以BD＝AC．
【解答】证明：∵线段AC与线段BD相交于点E，
∴∠AEB＝∠DEC，
在△ABE和△DCE中，
，
∴△ABE≌△DCE（ASA），
∴BE＝CE，
∴DE+BE＝AE+CE，
∴BD＝AC．
【点评】此题重点考查全等三角形的判定与性质、等式的性质等知识，正确地找到全等三角形的对应边和对应角并且证明△ABE≌△DCE是解题的关键．
22．（5分）如图，AB，CD相交于点O，DE∥AB．
（1）作∠BOD的角平分线OM，交DE于点F（要求：尺规作图，保留作图痕迹，不写作法）；
（2）若∠D＝60°，则△ODF的形状是 等边三角形 ．
【分析】（1）利用基本作图作∠BOD的平分线即可；
（2）先根据平行线的性质得到∠BOD＝120°，再根据角平分线的定义得到∠DOF＝60°，然后根据等边三角形的判定方法可判断△ODF的形状．
【解答】解：（1）如图，OF为所作；
（2）∵DE∥AB，
∴∠BOD+∠D＝180°，
∴∠BOD＝180°﹣60°＝120°，
∵OF平分∠BOD，
∴∠DOF＝60°，
∴△ODF为等边三角形．
故答案为：等边三角形．
【点评】本题考查了作图﹣基本作图：熟练掌握5种基本作图是解决问题的关键．也考查了平行线的性质和等边三角形的判定．
23．（5分）如图，为了满足A，B，C三个小区居民的体育锻炼需求，需要建立一个居民健身广场D，要使健身广场到三个小区的距离相等，请你在图中作出健身广场D的位置（要求：尺规作图，保留作图痕迹，不写作法）．
【分析】作线段BC，AC的垂直平分线交于点D，点D即为所求．
【解答】解：如图，点D即为所求．
【点评】本题考查作图﹣应用与设计作图，解题的关键是理解题意，灵活运用所学知识解决问题．
24．（5分）如图1，AD是△ABC的中线．
求证：AB+AC＞2AD．
请将下面的推理过程补充完整：
证明：如图2，延长AD到点E，使DE＝AD，连接BE．
∵AD是△ABC的中线，
∴BD＝CD．
在△ADC和△EDB中，
∴△ADC≌△EDB （ SAS ）．
∴ AC＝BE （全等三角形的对应边相等）．
∴在△ABE中，AB+BE＞AE （ 三角形两边之和大于第三边 ），
∴AB+AC＞AD+DE．
即AB+AC＞2AD．
【分析】由“SAS”可证△ADC≌△EDB，可得AC＝BE，由三角形的三边关系可求解．
【解答】证明：如图2，延长AD到点E，使DE＝AD，连接BE．
∵AD是△ABC的中线，
∴BD＝CD．
在△ADC和△EDB中，
，
∴△ADC≌△EDB （SAS）．
∴AC＝BE（全等三角形的对应边相等）．
∴在△ABE中，AB+BE＞AE （三角形两边之和大于第三边），
∴AB+AC＞AD+DE．
即AB+AC＞2AD．
故答案为：SAS，AC＝BE，三角形两边之和大于第三边．
【点评】本题考查了全等三角形的判定和性质，三角形的三边关系，证明三角形全等是解题的关键．
25．（6分）如图，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E，F，BE＝CF．求证：AD是△ABC的角平分线．
【分析】首先可证明Rt△BDE≌Rt△DCF（HL）再根据三角形角平分线的逆定理求得AD是角平分线即可．
【解答】证明：∵DE⊥AB，DF⊥AC，
∴Rt△BDE和Rt△CDF是直角三角形．
，
∴Rt△BDE≌Rt△CDF（HL），
∴DE＝DF，
∵DE⊥AB，DF⊥AC，AD＝AD，
∴Rt△ADE≌Rt△ADF（HL），
∴∠DAE＝∠DAF，
∴AD是△ABC的角平分线．
【点评】此题主要考查了角平分线的逆定理，综合运用了直角三角形全等的判定．由三角形全等得到DE＝DF是正确解答本题的关键．
26．（7分）在四边形ABCD中，∠A+∠C＝180°，BD平分∠ABC．
（1）如图1，若∠A＝90°．
①直接写出AD与CD的数量关系： AD＝CD ；
②请你写出图中一个与①不同的正确结论： AB＝CB ；
（2）如图2，若∠A＞90°，猜想AD与CD的数量关系，并证明．
【分析】（1）①由∠A+∠C＝180°，∠A＝90°，得∠A＝∠C＝90°，由BD平分∠ABC，∠ABD＝∠CBD，即可根据全等三角形的判定定理“AAS”证明△ABD≌△CBD，得AD＝CD；
②由△ABD≌△CBD，得AB＝CB，∠ADB＝∠CDB，则答案是AB＝CB，也可以是∠ADB＝∠CDB；
（2）作DF⊥BA交BA的延长线于点F，DE⊥BC于点E，则∠F＝∠CED＝90°，由∠BAD+∠DAF＝180°，∠BAD+∠C＝180°，得∠DAF＝∠C，根据角平分线的性质得DF＝DE，即可证明△ADF≌△CDE，得AD＝CD．
【解答】解：（1）①AD＝CD，
理由：如图1，∵∠A+∠C＝180°，∠A＝90°，
∴∠C＝90°，
∴∠A＝∠C，
∵BD平分∠ABC，
∴∠ABD＝∠CBD，
在△ABD和△CBD中，
，
∴△ABD≌△CBD（AAS），
∴AD＝CD，
故答案为：AD＝CD．
②AB＝CB，
理由：由①得△ABD≌△CBD，
∴AB＝CB，
故答案为：AB＝CB．
（2）AD＝CD，
证明：如图2，作DF⊥BA交BA的延长线于点F，DE⊥BC于点E，
∴∠F＝∠CED＝90°，
∵∠BAD+∠DAF＝180°，∠BAD+∠C＝180°，
∴∠DAF＝∠C，
∵BD平分∠ABC，DF⊥BA，DE⊥BC，
∴DF＝DE，
在△ADF和△CDE中，
，
∴△ADF≌△CDE（AAS），
∴AD＝CD．
注：（1）②答案不唯一，
可以是：∠ADB＝∠CDB，
理由：如图1，∵∠A+∠C＝180°，∠A＝90°，
∴∠C＝90°，
∴∠A＝∠C，
∵BD平分∠ABC，
∴∠ABD＝∠CBD，
在△ABD和△CBD中，
，
∴△ABD≌△CBD（AAS），
∴∠ADB＝∠CDB，
故答案为：∠ADB＝∠CDB．
【点评】此题重点考查角平分线上的点到角的两边的距离相等、同角的补角相等、全等三角形的判定与性质等知识，正确地作出辅助线得到△ABD和△CBD，并且证明△ABD≌△CBD是解题的关键．
27．（7分）如图，在等边△ABC中，点D是BC边上一点，作射线AD，点B关于射线AD的对称点为E，连接CE并延长交射线AD于点F．
（1）依题意补全图形；
（2）若∠BAF＝10°，则∠EFA的度数是 60° ；
（3）用等式表示线段AF，CF，EF之间的数量关系，并证明．
【分析】（1）根据题意画图即可；
（2）由轴对称可得∠BAF＝∠EAF，AB＝AE＝AC，根据等腰三角形的性质以及三角形内角和定理，可求出∠EFA的值；
（3）AF＝EF+CF；证明∠GAE＝∠FCB，进而可得∠CFA＝60°，用截长补短方法，在线段AF上作FG＝EF，连接GE，易得△EFG是等边三角形，再证明△CFB≌△AGE，即可证明AF＝EF+CF．
【解答】解：（1）如下图所示，
（2）∵△ABC是等边三角形，
∴AB＝AC，∠BAC＝∠ABC＝∠ACB＝60°，
∵∠BAF＝10°，∠ABC＝60°，
∴∠ADB＝180°﹣（∠BAF+∠ABC）＝180°﹣（10°+60°）＝110°，
∵点B关于射线AD的对称点为E，
∴AB＝AE＝AC，∠BAF＝∠EAF＝10°，
∴∠EAC＝∠BAC﹣（∠BAF+∠EAF）＝60°﹣（10°+10°）＝40°，
∵AE＝AC，
∴∠ACE＝（180°﹣∠EAC）＝（180°﹣40°）＝70°，
∵∠ACE＝∠ACB+∠DCF，∠ACB＝60°，
∴∠DCF＝∠ACE﹣∠ABC＝70°﹣60°＝10°，
∵∠ADB＝∠CDF＝110°，
∴∠EFA＝180°﹣（∠CDF+∠DCF）＝180°﹣（110°+10°）＝60°，
故答案为：60°；
（3）AF＝CF+EF，证明如下：
如下图所示，在线段AF上作FG＝EF，连接GE，
∵△ABC是等边三角形，
∴AB＝BC＝AC，∠BAC＝∠ABC＝∠ACB＝60°，
∵点B关于射线AD的对称点为E，
∴AB＝BC＝AE＝AC，∠BAF＝∠EAF，
∴△ABF≌△AEF，
∴BF＝EF，∠BFA＝∠EFA，
设∠BAF＝∠EAF＝α，则∠EAC＝∠BAC﹣（BAF+∠EAF）＝60°﹣2α，
∵AE＝AC，
∴∠ACF＝（180°﹣∠EAC）＝[180°﹣（60°﹣2α）＝60°+α，
∵∠ACF＝∠ACB+∠FCB，∠ACB＝60°，
∴∠FCB＝∠ACF﹣∠ACB＝60°+α﹣60°＝α，
∴∠FCB＝∠GAE＝∠BAF＝α，
∵∠CFA＝180°﹣（∠FAC+∠ACF），∠ACF＝60°+α，∠FAC＝∠BAC﹣∠BAF＝60°﹣α，
∴∠CFA＝180°﹣（60°+α+60°﹣α）＝60°，
∵∠BFA＝∠EFA，
∴∠CFB＝120°，
∵FG＝EF，∠CFA＝60°，
∴△EFG是等边三角形，
∴FG＝EF，∠FGE＝60°，
∴∠AGE＝180°﹣∠FGE＝180°﹣60°＝120°，
∴∠CFB＝∠AGE，
在△CFB和△AGE中，
，
∴△CFB≌△AGE（AAS），
∴CF＝AG，
∵AF＝FG+AG，CF＝AG，EF＝FG，
∴AF＝EF+CF．
【点评】本题考查了三角形的几何变换、等腰三角形和等边三角形的性质等，采用截长补短方法构造全等三角形是解本题的关键，综合性较强，难度较大．
28．（8分）在平面直角坐标系xOy中，点A，B，P不在同一直线上，对于点P和线段AB给出如下定义：过点P向线段AB所在直线作垂线，若垂足Q在线段AB上，则称点P为线段AB的内垂点，当垂足Q满足|AQ﹣BQ|最小时，称点P为线段AB的最佳内垂点．
已知点S（﹣3，1），T（1，1）．
（1）在点P1（2，4），P2（﹣4，0），P3（﹣2，），P4（1，3）中，线段ST的内垂点为 P3，P4 ；
（2）若点M是线段ST的最佳内垂点，则点M的坐标可以是 （﹣1，4），（﹣1，2） （写出两个满足条件的点M即可）；
（3）已知点C（m﹣2，3），D（m，3），若线段CD上的每一个点都是线段ST的内垂点，直接写出m的取值范围；
（4）已知点E（n+2，0），F（n+4，﹣1），若线段EF上存在线段ST的最佳内垂点，直接写出n的取值范围．
【分析】（1）利用图象法画出图形解决问题即可；
（2）满足条件的点在线段ST的中垂线上；
（3）构建不等式组解决问题即可；
（4）构建不等式组解决问题即可．
【解答】解：（1）如图1中，观察图象可知，线段ST的内垂点为P3，P4．
故答案为：P3，P4；
（2）如图，点M（﹣1，4），M′（﹣1，2）是线段ST的最佳内垂点，
故答案为：（﹣1，4），（﹣1，2）（答案不唯一）；
（3）由题意，，
解得﹣1≤m≤1．
故答案为：﹣1≤m≤1．
（4）如图2中，观察图象可知，m满足，
解得﹣5≤n≤﹣3．
【点评】本题考查坐标与图形的性质，垂线，线段的垂直平分线，不等式组等知识，解题的关键是理解题意，学会构建不等式组解决问题，属于中考常考题型．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2023/7/10 12:22:22；用户：笑涵数学；邮箱：15699920825；学号：36906111