2022-2023学年北京市石景山学校九年级（上）期中数学试卷【含解析】

这是一份2022-2023学年北京市石景山学校九年级（上）期中数学试卷【含解析】，共7页。试卷主要包含了填空题，解答题解答应写出文字说明等内容，欢迎下载使用。
1．如果3x＝4y（y≠0），那么下列比例式中正确的是（ ）
A．＝B．＝C．＝D．＝
2．如图，已知AB∥CD∥EF，BD：DF＝1：2，那么AC：AE的值是（ ）
A．B．C．D．2
3．抛物线y＝（x﹣2）2+1的顶点坐标是（ ）
A．（2，1）B．（﹣2，1）C．（﹣2，﹣1）D．（1，2）
4．若二次函数y＝kx2﹣4x﹣2与x轴有两个交点，则k的取值范围是（ ）
A．k＞﹣2B．k＞﹣2且k≠0C．k＜2D．k≥﹣2且k≠0
5．如图，点D在△ABC的边AC上，要判定△ADB与△ABC相似，添加一个条件，不正确的是（ ）
A．∠ABD＝∠CB．∠ADB＝∠ABCC．＝D．＝
6．正方形的面积y与它的周长x满足的函数关系是（ ）
A．正比例函数B．一次函数C．二次函数D．反比例函数
7．网球单打比赛场地宽度为8米，长度在球网的两侧各为12米，球网高度为0.9米（如图AB的高度）．中网比赛中，某运动员退出场地在距球网14米的D点处接球，设计打出直线穿越球，使球落在对方底线上C处，用刁钻的落点牵制对方．在这次进攻过程中，为保证战术成功，该运动员击球点高度至少为（ ）
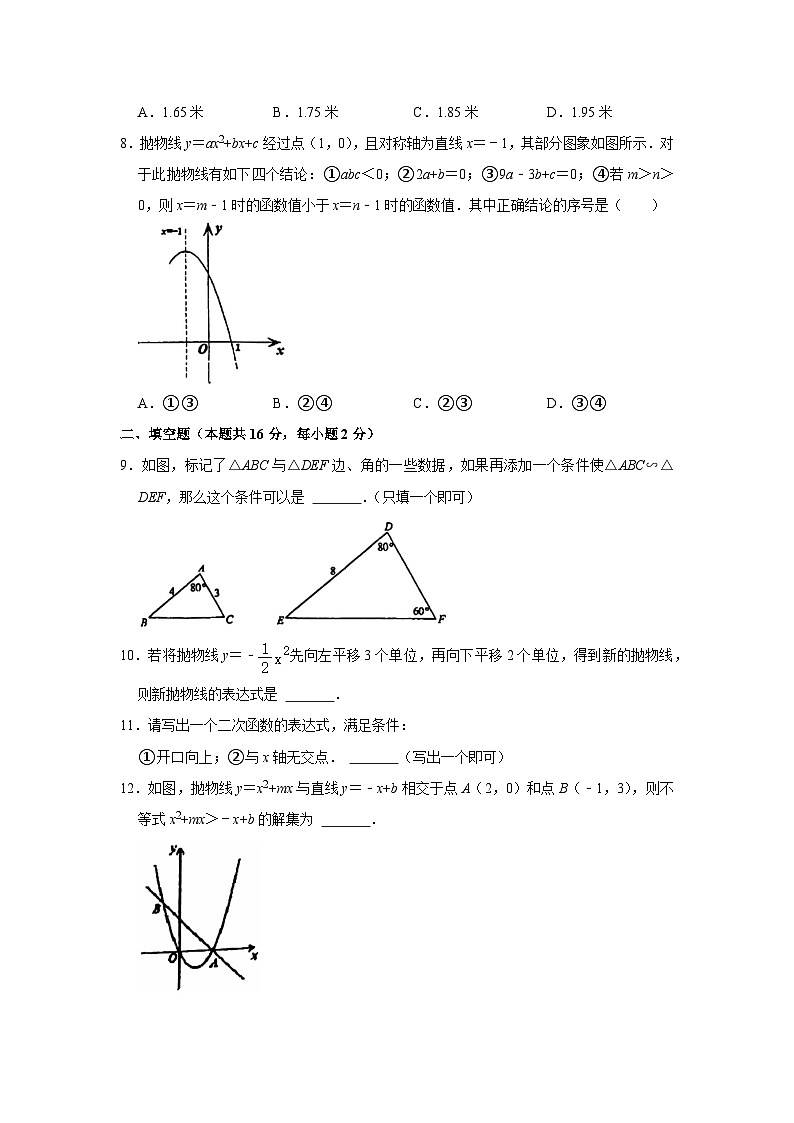
A．1.65米B．1.75米C．1.85米D．1.95米
8．抛物线y＝ax2+bx+c经过点（1，0），且对称轴为直线x＝﹣1，其部分图象如图所示．对于此抛物线有如下四个结论：①abc＜0；②2a+b＝0；③9a﹣3b+c＝0；④若m＞n＞0，则x＝m﹣1时的函数值小于x＝n﹣1时的函数值．其中正确结论的序号是（ ）
A．①③B．②④C．②③D．③④
二、填空题（本题共16分，每小题2分）
9．如图，标记了△ABC与△DEF边、角的一些数据，如果再添加一个条件使△ABC∽△DEF，那么这个条件可以是 ．（只填一个即可）
10．若将抛物线y＝﹣先向左平移3个单位，再向下平移2个单位，得到新的抛物线，则新抛物线的表达式是 ．
11．请写出一个二次函数的表达式，满足条件：
①开口向上；②与x轴无交点． （写出一个即可）
12．如图，抛物线y＝x2+mx与直线y＝﹣x+b相交于点A（2，0）和点B（﹣1，3），则不等式x2+mx＞﹣x+b的解集为 ．
13．A（﹣，y1），B（1，y2），C（4，y3）三点都在二次函数y＝﹣（x﹣2）2+k的图象上，则y1，y2，y3的大小关系为 ．（用“＜”号连接）
14．已知△ABC，DE∥BC，AD＝2，DB＝3，△ADE面积是4，则四边形DBCE的面积是 ．
15．如图，抛物线y＝ax2+bx+c的对称轴为x＝1，点P，点Q是抛物线与x轴的两个交点，若点P的坐标为（5，0），则点Q的坐标为 ．
16．对于二次函数y＝ax2和y＝bx2．其自变量与函数值的两组对应值如表所示：
根据二次函数图象的相关性质可知：m＝ ，d﹣c＝ ．
三、解答题（本题共68分，第17-25题，每小题6分，第26-27题，每小题6分）解答应写出文字说明、演算步骤或证明过程.
17．2tan60°﹣++|1﹣|．
18．解方程：x2﹣2x﹣8＝0．
19．如图，在△ABC中，D为AC边上一点，∠DBC＝∠A．
（1）求证：△BDC∽△ABC；
（2）若BC＝4，AC＝8，求CD的长．
20．如图，△ABO三个顶点的坐标分别为A（﹣2，4），B（﹣4，0），O（0，0），以原点O为位似中心，画出一个三角形，使它与△ABO的相似比为．
21．已知二次函数y＝x2+2x﹣3
（1）用配方法将其化为y＝a（x﹣h）2+k的形式；
（2）结合函数图象直接写出当y＞﹣3时，x的取值范围．
22．在平面直角坐标系xOy中，抛物线y＝﹣x2+2mx﹣m2+1的对称轴是直线x＝1．
（1）求抛物线的表达式：
（2）点D（n，y1），E（3，y2）．在抛物线上，若y1＜y2，请直接写出n的取值范围．
23．已知一个二次函数图象上部分点的横坐标x与纵坐标y的对应值如表所示：
（1）求这个二次函数的表达式；
（2）在给定的平面直角坐标系中画出这个二次函数的图象；
（3）结合图象，直接写出当﹣2＜x＜3时，y的取值范围．
24．某公园内人工湖上有一座拱桥（横截面如图所示），跨度AB为4米，在距点A水平距离为d米的地点，拱桥距离水面的高度为h米．小红根据学习函数的经验，对d和h之间的关系进行了探究．
下面是小红的探究过程，请补充完整：
（1）经过测量，得出了d和h的几组对应值，如表．
在d和h这两个变量中， 是自变量， 是这个变量的函数；
（2）在下面的平面直角坐标系xOy中，画出（1）中所确定的函数的图象；
（3）结合表格数据和函数图象，解决问题：
①桥墩露出水面的高度AE为 米；
②现公园欲开设游船项目，现有长为3.5米；宽为1.5米，露出水面高度为2米的游船．为安全起见，公园要在水面上的C、D两处设置警戒线，并且CE＝DF，要求游船能从C，D两点之间安全通过，则C距桥墩的距离CE至少为 米．（精确到0.1米）
25．已知关于x的二次函数y＝x2﹣2tx+2．
（1）求该抛物线的对称轴（用含t的式子表示）；
（2）若点M（t﹣3，m），N（t+5，n）在抛物线上，则m n；（用“＜”，“＝”或“＞”填空）
（3）P（x1，y1），Q（x2，y2）是抛线上的任意两个点，若对于﹣1≤x1＜3且x2＝3，都有y1≤y2，求t的取值范围．
26．在等腰直角△ABC中，AB＝AC，∠BAC＝90°，过点B作BC的垂线l．点P为直线AB上的一个动点（不与点A，B重合），将射线PC绕点P顺时针旋转90°交直线l于点D．
（1）如图1，点P在线段AB上，依题意补全图形；
①求证：若∠BDP＝∠PCB；
②用等式表示线段BC，BD，BP之间的数量关系，并证明．
（2）点P在线段AB的延长线上，直接写出线段BC，BD，BP之间的数量关系．
27．对于平面直角坐标系xOy中第一象限内的点P（x，y）和图形W，给出如下定义：过点P作x轴和y轴的垂线，垂足分别为M，N，若图形W中的任意一点Q（a，b）满足a≤x且b≤y，则称四边形PMON是图形W的一个覆盖，点P为这个覆盖的一个特征点．例：已知A（1，2），B（3，1），则点P（5，4）为线段AB的一个覆盖的特征点．
（1）已知点C（2，3），
①在P1（1，3），P2（3，3），P3（4，4）中，是△ABC的覆盖特征点的为 ；
②若在一次函数y＝mx+5（m≠0）的图象上存在△ABC的覆盖的特征点，求m的取值范围．
（2）以点D（2，4）为圆心，半径为1作圆，在抛物线y＝ax2﹣5ax+4（a≠0）上存在⊙D的覆盖的特征点，直接写出a的取值范围 ．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2023/7/11 11:34:44；用户：笑涵数学；邮箱：15699920825；学号：36906111x
﹣1
m（m≠﹣1）
y＝ax2
c
c
y＝bx2
c+3
d
x
…
﹣1
0
1
2
3
…
y
…
0
3
4
3
0
…
d（米）
0
0.6
1
1.8
2.4
3
3.6
4
h（米）
0.88
1.90
2.38
2.86
2.80
2.38
1.60
0.88