
所属成套资源:新高考数学三轮冲刺卷 (含解析)
新高考数学三轮冲刺卷:一次函数与二次函数(含解析)
展开这是一份新高考数学三轮冲刺卷:一次函数与二次函数(含解析),共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题(共20小题;)
1. 函数 , 的值域是
A. B. C. D.
2. 函数 在 上有最大值 ,则实数
A. 或 B. C. 或 D.
3. 函数 在区间 上是增函数,则实数 的取值范围是
A. B. C. D.
4. 如果函数 在区间 上单调递减,则实数 满足的条件是
A. B. C. D.
5. 若函数 的定义域为 ,值域为 ,则 的取值范围是
A. B. C. D.
6. 函数 的单调减区间是
A. B. C. D.
7. 若二次函数 满足:① 是偶函数;②在 轴上截得的弦长为 ;与函数 的图象有两个不同的交点,则实数 的取值范围是
A. B. C. D.
8. 已知二次函数 ,满足 ,且在区间 上的最大值为 ,若函数 有唯一零点,则实数 的取值范围是
A. B.
C. D.
9. 对于实数 和 ,定义运算“”:,设 ,且关于 的方程 有三个互不相等的实根 ,,,则 的取值范围是
A. B. C. D.
10. 给出以下命题:①函数 在 时是增函数, 时也是增函数,所以 是增函数;②若函数 与 轴没有交点,则 且 ;③ 的递增区间为 ;④ 和 表示相等函数.
其中正确命题的个数是
A. 个B. 个C. 个D. 个
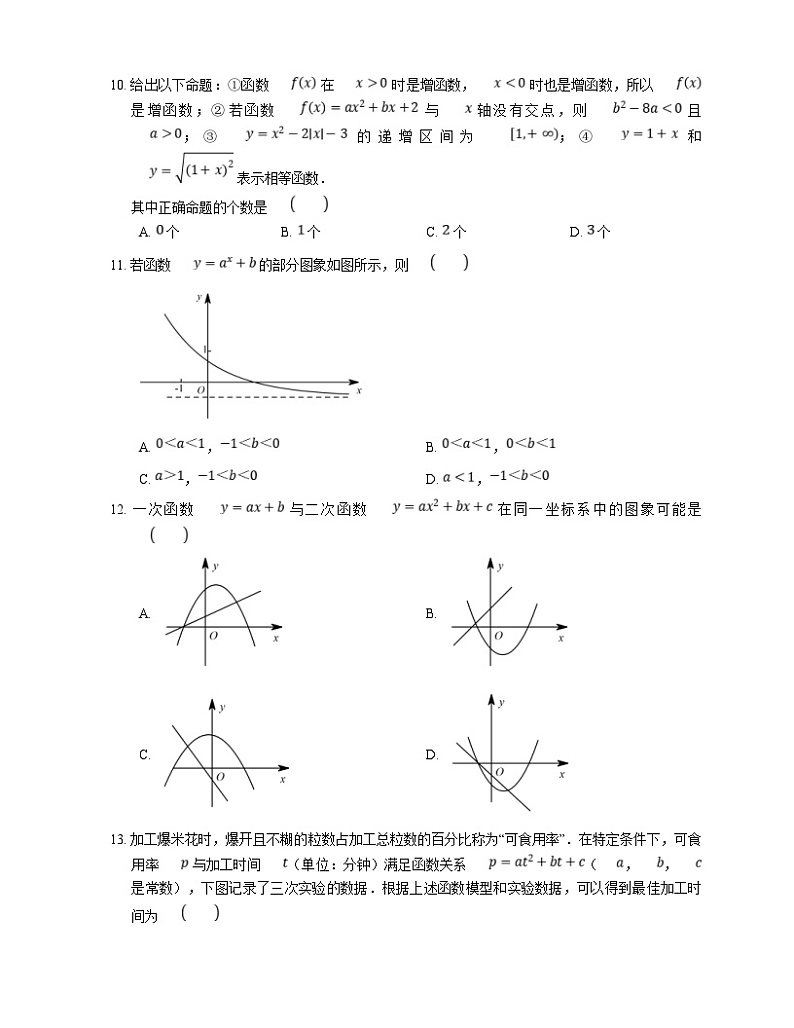
11. 若函数 的部分图象如图所示,则
A. ,B. ,
C. ,D. ,
12. 一次函数 与二次函数 在同一坐标系中的图象可能是
A. B.
C. D.
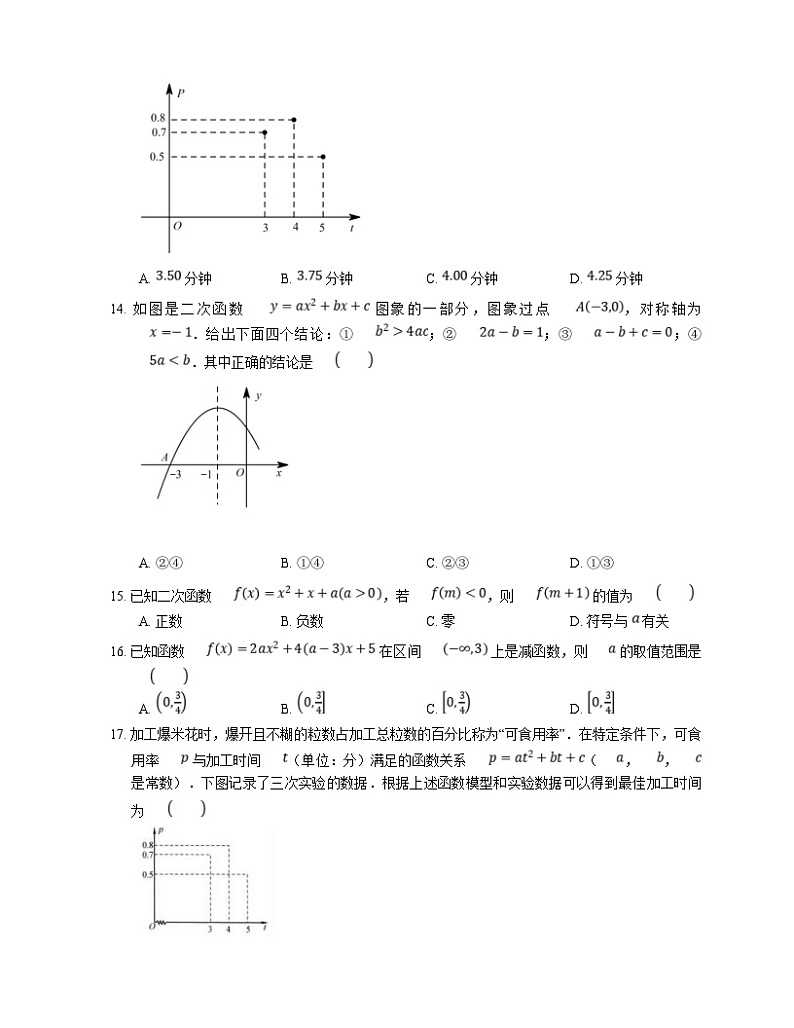
13. 加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率 与加工时间 (单位:分钟)满足函数关系 (,, 是常数),下图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为
A. 分钟B. 分钟C. 分钟D. 分钟
14. 如图是二次函数 图象的一部分,图象过点 ,对称轴为 .给出下面四个结论:① ;② ;③ ;④ .其中正确的结论是
A. ②④B. ①④C. ②③D. ①③
15. 已知二次函数 ,若 ,则 的值为
A. 正数B. 负数C. 零D. 符号与 有关
16. 已知函数 在区间 上是减函数,则 的取值范围是
A. B. C. D.
17. 加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率 与加工时间 (单位:分)满足的函数关系 (,, 是常数).下图记录了三次实验的数据.根据上述函数模型和实验数据可以得到最佳加工时间为
A. 分B. 分C. 分D. 分
18. 设 ,,,,, 都是非零实数,不等式 的解集为 ,不等式 的解集为 ,则“”是“”的
A. 充分非必要条件B. 必要非充分条件
C. 充分必要条件D. 既非充分又非必要条件
19. 函数 ,,若存在 ,使得 ,则 的最大值为
A. B. C. D.
20. 已知函数 ,若 ,则 的取值范围是
A. B. C. D.
二、填空题(共5小题;)
21. 定义:如果在函数 定义域内的给定区间 上存在 ,满足 ,则称函数 是 上的“平均值函数”, 是它的一个均值点,如 是 上的平均值函数, 就是它的均值点.现有函数 是 上的平均值函数,则实数 的取值范围是 .
22. 已知函数 ,.若对任意 ,总存在 ,使得 成立,则实数 的值为 .
23. 已知函数 ,,且函数 的最小值为 ,则 的取值范围是 .
24. 已知函数 .若存在 ,使得关于 的方程 有三个不相等的实数根,则实数 的取值范围是 .
25. 已知函数 ,,若 ,则 的最小值为 ;若函数 的最小值为 ,则 的取值范围是 .
三、解答题(共5小题;)
26. 已知二次函数 满足 和 .
(1)求函数 的解析式;
(2)求函数 在区间 上的最大值和最小值.
27. 已知函数 .
(1)若 ,求函数的值域.
(2)若 ,求函数的最小值.
28. 函数 在区间 上有最小值 ,求 的值.
29. 已知函数 .
(1)若对任意的实数 都有 成立,求实数 的值;
(2)若 在区间 上为单调递增函数,求实数 的取值范围;
(3)当 时,求函数 的最大值.
30. 学校食堂改建一个开水房,计划用电炉或煤炭烧水,但用煤时也要用电鼓风及时排气,用煤烧开水每吨开水费为 元,用电炉烧开水每吨开水费为 元,,.其中 为毎吨煤的价格, 为每百度电的价格,如果烧煤时的费用不超过用电炉时的费用,则仍用原备的锅炉使用煤炭烧水,否则就用电炉烧水.
(1)如果两种方法烧水费用相同,试将每吨煤的价格表示为每百度电价的函数;
(2)如果每百度电价不低于 元,则用煤烧水时每吨煤的最高价是多少?
答案
1. B
2. D
3. D
4. A【解析】函数图象的对称轴为 ,由题意得 ,解得 .
5. C
【解析】函数 的图象是开口向上,且以直线 为对称轴的抛物线,
所以 ,,
因为函数 的定义域为 ,值域为 ,
所以 ,即 的取值范围是 .
故选:C.
6. A【解析】,当 时, 为增函数,当 时, 是函数 的增区间; 是函数 的减区间.
7. D【解析】根据题意得 的对称轴为 ,且过 和 两点,
所以
所以
所以 ,
因为 与 的图象有两个不同的交点,
所以 有两个解,
则有
由①得:,
由②得:,
所以 或
解得 ,
又因为 与 不同时为 时也成立,
所以当 时,解得 ,
此时,,成立,
当 时,解得 ,
此时 ,不成立.
综上所述, 的取值范围为 .
8. C【解析】二次函数 ,满足 ,
可得直线 为函数 的对称轴,
即有
由 在区间 上的最大值为 ,
当 时, 在 上单调递减,在 时取得最大值
当 时, 在 上单调递增,在 时取得最大值 ,所以此情况不成立.
由①②解得 ,.
则 ,
若函数 有唯一零点,
即为方程 有唯一实根,
作出 的图象和直线 的图象,
当 ,有 与 有两个交点,舍;
当 时,由 ,
即有 ,
由判别式 ,
解得 .
由图象可得 时, 的图象和直线 的图象有两个交点,舍;
当 时, 的图象和直线 的图象有三个交点,舍;
当 时,且 为曲线 的切线时,只有一个交点,即为原点,
,
可得 即 只有相等的两实根,
可得判别式 ,
解得 ,
由图象可得 时, 的图象和直线 的图象只有一个交点,即为原点.
综上可得,所求 的范围为 .
9. A
10. A
11. A
12. C【解析】若 ,则一次函数 为增函数,二次函数 的开口向上,故可排除 A;
若 ,一次函数 为减函数,二次函数 开口向下,故可排除 D;
对于选项B,看直线可知 ,,从而 ,而二次函数的对称轴在 轴的右侧,故应排除B.
13. B【解析】由已知得 解得
所以 ,
所以当 时, 最大,
即最佳加工时间为 分钟.
14. B【解析】因为二次函数的图象与 轴交于两点,所以 ,即 ,①正确;
对称轴为 ,即 ,,②错误;
结合图象,当 时,,即 ,③错误;
由对称轴为 知,,又函数图象开口向下,所以 ,所以 ,即 ,④正确.
15. A
【解析】因为 ,所以 ,
又因为函数的对称轴为 ,所以 ,
又因为 ,所以 ,所以 ,
所以 .
16. D【解析】当 时,,在 上是减函数;当 时,由 得 ,综上 的取值范围是 .
17. B
18. B
19. C【解析】记 ,
最小值为 ,最大值为 ,
由 ,
得 ,
要求 的值最大, 取最大值, 取最小值,
得 ,所以 .
20. D
【解析】由题意作出函数 和 的图象.
由图象得,函数 在图象为经过原点的直线,当直线 介于直线 和 轴之间时与题意相符,直线 为曲线的切线,且此时 在第二象限的解析式为 ,导数为 ,因为 ,所以 ,故直线 的斜率为 ,所以只需直线 的斜率 介于 与 之间即可,即 .
21.
【解析】因为函数 是 上的平均值函数,
设 为均值点,
所以 ,
即关于 的方程 在 内有实数根,
解方程得 或 ,
所以必有 ,即 ,
所以实数 的取值范围是 .
22.
【解析】因为 在 上单调递减,
所以 ,
解法 :由题意得,,即 在 上恒成立,
即 ,在 上恒成立,
所以 即 在 上恒成立,
所以 ,.
解法 :,
因为 ,
所以 即
解得 .
23.
【解析】函数 的对称轴为 ,
若当 时,函数 的最小值为 ,则 .
故答案为: 的取值范围是 .
24.
【解析】由题意得 ,且关于 的方程 有三个不相等的实数根.
()当 时,,且 ,
可知 在 上是增函数,此时关于 的方程 不可能有三个不相等的实数解;
()当 时,,
可知 在区间 , 上分别是增函数,而在区间 上是减函数(如图所示).
当且仅当 时,方程 有三个不相等的实数解.
即 .
令 ,则 在 时是增函数,则得 .
所以,所求实数 的取值范围是 .
25. ,
【解析】若 ,函数 ,
当 时, 的最小值为 ,
若函数 在 上的最小值为 ,
则 在 上单调递减,
所以 ,即此时 的取值范围为 .
26. (1) 设 ,
因为 ,
所以 .
又因为 ,
所以 ,而 .
所以 ,这是一 个恒等式,
所以
解得
所以 .
(2) 解法一:由 .
因为 ,
所以 ,
所以 ,
所以函数 在区间 上 的最大值和最小值分别为 ,.
解法二:画出函数 的示意图(如图).
由图可知函数 在 时取得最小值 ,
在 时 取是最大值 ,
所以函数 在区间 上的最大值和最小值 分别为 和 .
27. (1) 若 ,则 ,,
所以 的值域为 .
(2) ,,
对称轴 ,函数 开口向上,
①当 时,即 时,;
②当 时,即 时,;
③当 时,即 时,.
综上,当 时,;
当 时,;
当 时,.
28. ,
①当 ,即 时,函数 在 上单调递增.
所以 ,
由 ,得 ,
因为 ,
所以 .
②当 ,即 时,,
由 ,得 ,舍去.
③当 ,即 时,函数 在 上单调递减,
,
由 ,得 ,
因为 ,
所以 .
综上所述, 或 .
29. (1) 由对任意的实数 都有 成立,
知函数 的对称轴 ,即 .
(2) 函数 的图象的对称轴为直线 ,
由 在 上为单调递增函数,
在区间 上为单调递增函数,得 ,
即 的取值范围是 .
(3) 函数图象开口向上,对称轴 ,可得最大值只能在端点处取得.
当 时, 时,函数取得最大值为 ;
当 时, 时,函数取得最大值为 ;
当 时, 时,函数取得最大值为 .
30. (1) 依题意,得 ,
即 .
(2) 由 ,得 .
不妨令 ,则 ,则 .
因为 ,所以 ,即 .
所以当 时,,此时 .
答:每吨煤的最高价为 元.
相关试卷
这是一份新高考数学三轮冲刺卷:空间的垂直关系(含解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份新高考数学三轮冲刺卷:空间几何量(含解析),共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份新高考数学三轮冲刺卷:直线综合(含解析),共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












