新高考数学三轮冲刺卷：空间向量（含解析）

这是一份新高考数学三轮冲刺卷：空间向量（含解析），共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共20小题；）
1. 若向量 ，，且 与 的夹角余弦为 ，则 等于
A. B. C. D.

2. 设点 是 轴上一点，且点 到 与点 的距离相等，则点 的坐标是
A. B.
C. D.

3. 平面 的法向量为 ，平面 的法向量为 ，若 ，则 等于
A. B. C. D.

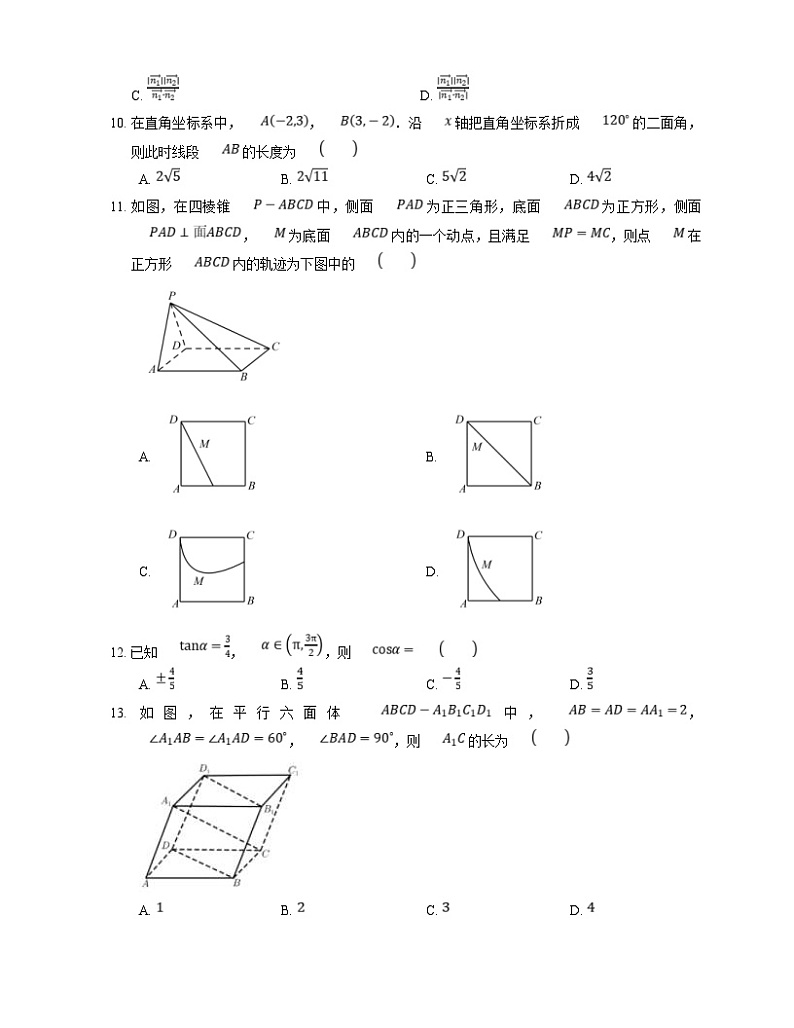
4. 已知平面 内有一个点 ，平面 的一个法向量是 ，则下列点 中在平面 内的是
A. B. C. D.

5. 已知向量 ， 则下列向量中与 成 夹角的是
A. B. C. D.

6. 正方形 的边长为 ， 平面 ，， 、 分别是 、 的中点，那么直线 与 所成角的余弦值是
A. B. C. D.

7. 已知 ，，，若 ，则
A. B. C. D.

8. 下列说法中正确的是
A. 任何三个不共线的向量可构成空间向量的一个基底
B. 空间的基底有且仅有一个
C. 两两垂直的三个非零向量可构成空间的一个基底
D. 基底 ，， 中基向量与基底 ，， 中基向量对应相等

9. 设平面 与平面 的夹角为 ，若平面 ， 的法向量分别为 和 ，则
A. B.
C. D.

10. 在直角坐标系中，，．沿 轴把直角坐标系折成 的二面角，则此时线段 的长度为
A. B. C. D.

11. 如图，在四棱锥 中，侧面 为正三角形，底面 为正方形，侧面 ， 为底面 内的一个动点，且满足 ，则点 在正方形 内的轨迹为下图中的

A. B.
C. D.

12. 已知 ，，则
A. B. C. D.

13. 如图，在平行六面体 中，，，，则 的长为
A. B. C. D.

14. 已知两非零向量 ，，且 与 不共线，设 （，且 ），则
A. B.
C. 与 ， 共面D. 以上三种情况均有可能

15. 如图，在空间四边形 中，，，，点 为 的中点，点 为 的中点，则 等于
A. B.
C. D.

16. 如图，在平行六面体 中， 为 与 的交点，若 ，，，则下列向量中与 相等的向量是
A. B. C. D.

17. 已知空间向量 ， 满足 ，且 ， 的夹角为 ， 为空间直角坐标系的原点，点 ， 满足 ，，则 的面积为
A. B. C. D.

18. 在空间坐标系 中，已知 ，，，，若 ，， 分别表示三棱锥 在 ，， 在坐标平面上的正投影图形的面积，则
A. B. 且
C. 且 D. 且

19. 已知三点 ， ， ，则
A. 三点构成等腰三角形B. 三点构成直角三角形
C. 三点构成等腰直角三角形D. 三点构不成三角形

20. 已知 ，，，若 ，， 三向量共面，则实数 等于
A. B. C. D.

二、填空题（共5小题；）
21. 已知向量 ， ，若 与 成 角，则 ．

22. 已知向量 ，，，且 ，则 ．

23. 设空间向量 ， 均为单位向量，且与向量 的夹角都等于 ，则 ．

24. 若 ， 与 、 与 的夹角均为 ，，，，则 ．

25. 设向量 与向量 互相垂直，向量 与它们构成的角均为 且 ，，，则 ．

三、解答题（共5小题；）
26. 设 ，，，且 ，，，求向量 的模．

27. 已知 、 、 是空间中不共面的三个向量，，，，求证：向量 ，， 共面．

28. 如图，在正四棱柱 中，，，，，， 分别是 ，，， 的中点．求证：．

29. 如图所示，正方体 的棱长为 ，在三棱锥 中，求 到平面 的距离 ．

30. 如图，在长方体 中，，，，证明直线 平行于平面 ，并求直线 到平面 的距离．
答案
1. C【解析】因为
所以 ．
2. B
3. C【解析】因为 ，所以两平面法向量平行，所以 ，所以 ．
4. A
5. B
6. A
7. B
8. C【解析】A 项中应是不共面的三个向量构成空间向量的基底；
B 项，空间基底有无数个；
D 项中因为基底不惟一，所以 D 错．
9. B
10. B
【解析】如图，作 垂直 轴， 垂直 轴，过 作 平行于 轴，与 交于 ，则 就是二面角的平面角．
，连接 ，则 ，，，在 中，， ．
11. A
12. C【解析】因为 ，，
所以 ．
又因为 ，
所以 ，
整理得 ，
解得 ．
因为 ，
所以 ，故 ．
13. B【解析】因为 ，
所以 ，
所以 ，
所以 ，
，
．
14. C【解析】假设 与 共线，则设 ，
所以 可变为 ，
所以 与 共线，这与 与 不共线相矛盾，故假设不成立，
即 A 项不正确，同理 B 项不正确，则 D 项也错误，故选 C．
15. B
【解析】
16. A【解析】提示：．
17. B【解析】，同理 ，
则 ，
从而有 ，
所以 的面积 ．
18. D【解析】 在平面上的投影为 ，故 ．
设 在 和 平面上的投影分别为 和 ，则 在 和 平面上的投影分别为 和 ，
因为 ，，
故 ．
综上，选项D正确．
19. D
20. D
【解析】因为 ，， 三向量共面，所以有 ，即 解得 所以 ．
21.
22.
23.
24.
25.
【解析】提示：．
26.
所以 ．
27. 设 ，则 ，
所以 解得
所以 ，
所以向量 ，， 共面．
28.
如图，建立空间直角坐标系 ，可得 ，，，，，，，，，．
平面 的一个法向量为 ，，，
所以
令 ，得 ，，．
设平面 的一个法向量为 ．
，，
所以
令 ，得 ，，．
因为 ，
所以平面 ．
29. 在三棱锥 中， 是三棱锥 的高，，，
因为 ，
所以 ．
30. 因为 为长方体，故 ，，
故 为平行四边形，故 ，显然 不在平面 上，
于是直线 平行于平面 ；
直线 到平面 的距离即为点 到平面 的距离，设为 ．
考虑三棱锥 的体积，以 为底面，可得
而 中，，，故
所以，
即直线 到平面 的距离为 ．