初中数学人教版（2024）七年级上册（2024）6.3 角教学课件ppt

这是一份初中数学人教版（2024）七年级上册（2024）6.3 角教学课件ppt，共25页。PPT课件主要包含了学习目标，知识导入，探究新知，归纳总结，应用新知，余角的性质，补角的性质，同角或等角的补角相等，同角或等角的余角相等，例题练习等内容，欢迎下载使用。

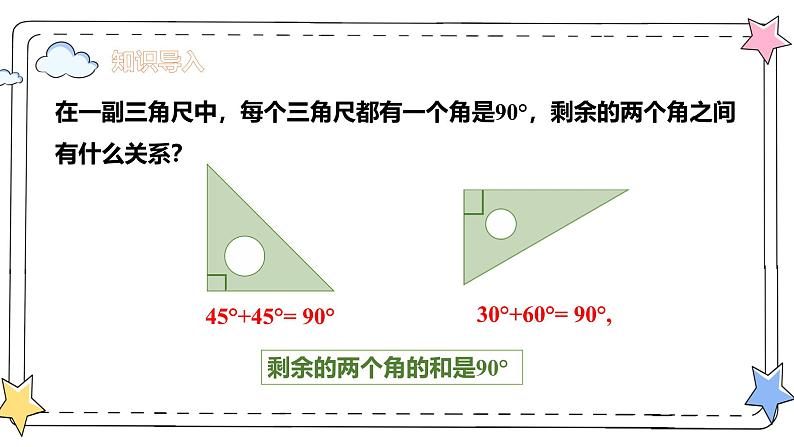
在一副三角尺中，每个三角尺都有一个角是90°，剩余的两个角之间有什么关系？
剩余的两个角的和是90°
30°+60°= 90°,
45°+45°= 90°
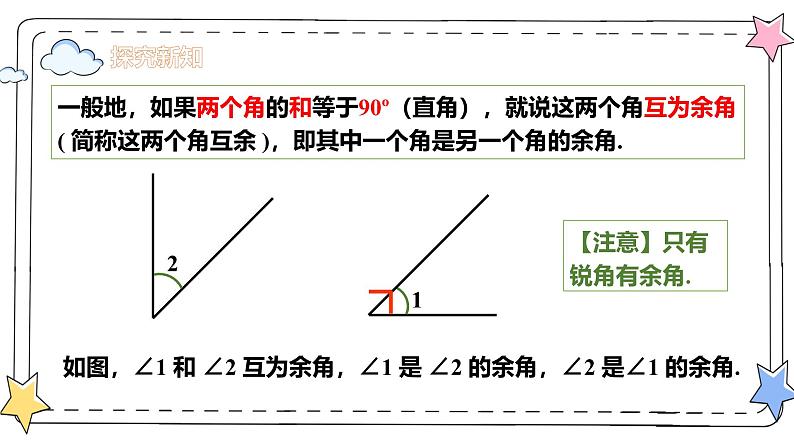
一般地，如果两个角的和等于90º（直角），就说这两个角互为余角( 简称这两个角互余 )，即其中一个角是另一个角的余角.
如图，∠1 和 ∠2 互为余角，∠1 是 ∠2 的余角，∠2 是∠1 的余角.
【注意】只有锐角有余角.
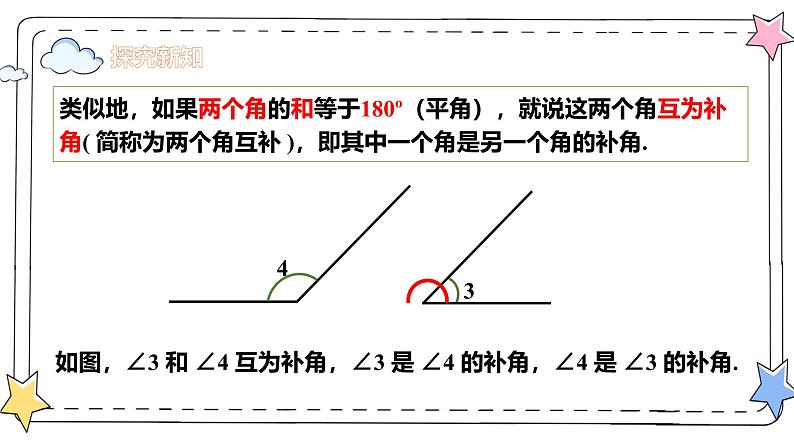
类似地，如果两个角的和等于180º（平角），就说这两个角互为补角( 简称为两个角互补 )，即其中一个角是另一个角的补角.
如图，∠3 和 ∠4 互为补角，∠3 是 ∠4 的补角，∠4 是 ∠3 的补角.
如果两个角的和等于180º（平角），就说这两个角互为补角( 简称为两个角互补 )，即其中一个角是另一个角的补角.
【注意】1.余角（补角）是成对出现的；2.两个角互余（互补）是两个角之间的数量关系，只与它们的度数有关，与它们的位置无关.
【思考】∠1 与∠2，∠3都互为余角，∠2 与∠3 的大小有什么关系？
因为∠1 与∠2，∠3 都互为余角，
即∠2 = 90° - ∠1，∠3 = 90° - ∠1.
所以∠2 = ∠3 .
所以∠1+∠2 = 90°，∠1+∠3 = 90°
同角 (等角) 的余角相等．
【思考】∠1 与∠2，∠3 都互为补角，∠2 与∠3 的大小有什么关系？
因为∠1 与∠2，∠3 都互为补角，
即∠2 = 180° - ∠1，∠3 = 180° - ∠1.
所以∠1+∠2 = 180°，∠1+∠3 = 180°
同角 (等角) 的补角相等．
∠1 +∠2 = 90°
或∠1 = 90° -∠2
∠1 +∠2 = 180°
或∠1 = 180° -∠2
【分析】互为余角的两个角的和是90°，而已知条件中隐含互为补角的条件，再利用角平分线的条件，便可以发现互为余角的角.
如图，点 A，O，B 在同一条直线上，射线 OD 和射线 OE 分别平分∠AOC 和∠BOC，图中哪些角互为余角？
解：因为点 A，O，B 在同一条直线上，所以∠AOC 和∠BOC 互为补角．
又因为射线 OD 和射线 OE 分别平分∠AOC 和∠BOC，
所以∠COD 和 ∠COE 互为余角，同理，∠AOD 和∠BOE，∠AOD 和∠COE，∠COD 和∠BOE 互为余角．
∠EOC, ∠BOD, ∠BOC
有，分别是∠BOF, ∠COE.