人教版八(上) 第11章 三角形 章末复习 课件

这是一份人教版八(上) 第11章 三角形 章末复习 课件，共36页。

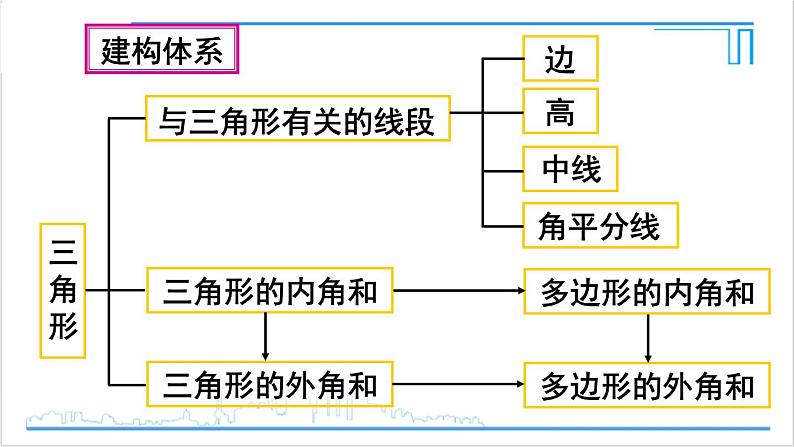
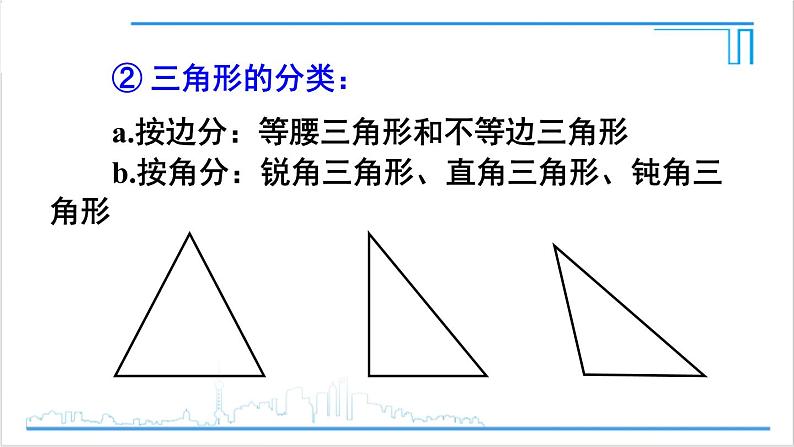
章末复习R·八年级上册虽说我们从小学开始，就零零散散地学习了一些三角形的知识，但系统地学习三角形的知识，是从本章开始的，下面我们再一起回顾一下本章的知识要点和几何研究方法.复习目标： 1．梳理三角形和多边形有关的知识点. 2．了解三角形与多边形的内在联系. 问题1 　请同学们回答下列问题：（1）三角形的三边之间有怎样的关系？得出这个结论的依据是什么？（2）三角形的三个内角之间有怎样的关系？如何证明这个结论？梳理知识问题1 　请同学们回答下列问题：（3）直角三角形的两个锐角之间有怎样的关系？三角形的一个外角和它不相邻的两个内角之间有怎样的关系？这些结论能由三角形内角和定理得出吗？（4）n 边形的n 个内角有怎样的关系？如何推出这个结论？（5）n 边形的外角大小和与n 有关吗？为什么？建构体系① 三角形的定义a.边：组成三角形的线段b.顶点：相邻两边的交点c.角：相邻两边组成的角d.表示法：△ABC② 三角形的分类：a.按边分：等腰三角形和不等边三角形b.按角分：锐角三角形、直角三角形、钝角三角形③ 三角形的主要线段：a.三角形的中线：连接三角形的一个顶点和它对边中点的线段叫做三角形的中线.b.三角形的角平分线：三角形一个内角的平分线与它的对边相交，这个角的顶点与对边上的交点之间的线段，叫做三角形的角平分线.c.三角形的高：从三角形的一个顶点向它的对边作垂线，所得线段叫做三角形的高.④三角形三边间的关系：三角形两边的和大于第三边.⑤三角形的稳定性及应用：三角形具有稳定性.⑥多边形的对角线、内角和、外角和：n 边形的对角线条数等于 ，内角和等于（n-2）·180°，外角和等于360°.课堂练习　　A 组　复习与三角形有关的线段：1．若三角形的两边分别为 3 和 5 ，则第三边长m 的取值范围是__________． 2 < m < 8　　A 组　复习与三角形有关的线段：2．如图： （1）若AD ⊥BC，垂足 为D，则： ∠_____ =∠_____ = 90°；ADBADC　　A 组　复习与三角形有关的线段：2．如图： （2）若∠BAE =∠CAE， AE 与BC 相交于点 E，则： 线段AE 是△ABC 的_________；角平分线BF　　A 组　复习与三角形有关的线段：2．如图： （3）若AF =CF，BF 与 AC 相交于点F， 则：△ABC 的中 线是 ．　　B 组　巩固与三角形有关的角：　　如图，在△ABC 中，∠BAC =80°，∠ABC =60°. （1）∠C =　　　　；（2）若AE 是△ABC 的　　 角平分线，则： ∠AEC = ；（3）若BF 是△ABC 的 高，与角平分线 AE 相交于点O，则∠EOF =　　 ．40°100°130°　　例1 已知等腰三角形的两边长分别为10 和6 ，则三角形的周长是　　　　　．　　变式1 若等腰三角形的周长为20，一边长为4，则其他两边长为　　　　　．22或268和8典型例题　　变式2　小明用一条长20 cm的细绳围成了一个等腰三角形，他想使这个三角形的一边长是另一边长的2倍，那么这个三角形的各边的长分别是多少？解：设较短的边长为 x cm，则较长的边长为2x cm． 若较短的边为腰，则 x + x + 2x =20. 解得　x =5．　　即　2x =10． 因为 5 + 5 =10，不符合三角形两边的和大于第　三边，所以不能围成腰长5 cm的等腰三角形．解：若较长的边为腰，则 x + 2x + 2x =20. 解得　x = 4．　　所以，这个三角形的三边分别为：　　4 cm， 8 cm， 8 cm．　　变式2　小明用一条长20 cm的细绳围成了一个等腰三角形，他想使这个三角形的一边长是另一边长的2倍，那么这个三角形的各边的长分别是多少？　　例2　如图，在△ABC 中，∠ ABC ，∠ ACB 的平分线BD，CE 交于点O．　　若∠ABC =40°，∠ACB =60°，则：∠BOC = 　　 ．130°　　例2　如图，在△ABC 中，∠ ABC ，∠ ACB 的平分线BD，CE 交于点O． 变式1　若∠A =80°，则∠BOC = ．　 变式2　你能猜想出∠BOC 与∠A 之间的数量关系吗？ 130°　　变式3　如图，若换成两外角平分线相交于O，则∠BOC 与∠A 又有怎样的数量关系？　　变式4　如图，若换成一内角与一外角平分线相交于点O，则∠BOC与∠A 又有怎样的数量关系？　　变式5　如图，若换成两条高相交于点O， ∠A 与∠BOC 又有怎样的数量关系？ 　　∠BOC = 180°-∠A　　练习1（1）三角形的两边分别为 3 和 5，则三角形周长 y 的范围是（ ）A.2＜y＜8 B.10＜y＜18C.10＜y＜16 D.无法确定C　　练习1（2）在下列条件中：① ∠A + ∠B =∠C，②∠A：∠B：∠C =1：2：3，③∠A = 90°－∠B，④∠A =∠B =∠C中，能确定△ABC是直角三角形的条件有（ ）A.1个 B.2个 C.3个 D.4个C　　练习1（3）已知一个多边形的内角和是外角和的2倍，则这个多边形的边数为______.6练习2 已知三角形的两个外角分别为a°，b°，且满足（a－50）2 =－|a+b－200|，求此三角形各角的度数.解:∵（a-50）2+|a+b-200|=0，∴其中两内角为130°，30°，另一个内角为20°.练习3 三角形的最长边为10，另两边的长分别为 x 和 4，周长为 c，求 x 和 c 的取值范围.解：根据三角形两边之和大于第三边、两边之差小于第三边.又最长边为10，得x 的取值范围.10-4＜x＜10 ∴6＜x＜10.又c = 10+4+x = x+14，∴20＜c＜24.1.已知a、b、c是三角形的三边长，化简：|a－b＋c|－|a－b－c|=_________.2a－2b基础巩固2.如图，在直角三角形ABC中，∠ACB =90°，CD是AB边上的高，AB = 13cm，BC = 12cm，AC = 5cm.综合应用（1）求出△ABC的面积及 CD的长；（2）已知BE是 △ABC的边AC上的中线，求出△ABE的面积.解：3.一轮船由B 处向C处航行，在B 处测得C处在B 的北偏东75°方向上，在海岛上的观察所A 测得B 在A 的南偏西30°方向，C 在A的南偏东25°方向；若轮船行使到C 处，那么从C 处看A、B 两处的视角∠ACB是多少度？拓展延伸解：根据题意，画出示意图如图所示：另求出∠ABC =75°- 30°= 45°，∠BAC = 30°+25°= 55°，所以∠ACB =180°- 45°- 55°= 80°.1.从课后习题中选取；2.完成练习册本课时的习题。