初中人教版（2024）12.2 三角形全等的判定精品课件ppt

这是一份初中人教版（2024）12.2 三角形全等的判定精品课件ppt，共27页。PPT课件主要包含了知识点1，解决实际问题，知识点2，∴CECD，基础巩固，BCEF，综合应用，∠A∠D，∠ACB∠F，拓展延伸等内容，欢迎下载使用。

一张教学用的三角形硬纸板不小心被撕坏了，如图，你能制作一张与原来形状大小相同的三角形硬纸板吗？下面我们带着这个问题学习判定三角形全等的两个重要方法.
学习目标： 1．能叙述出“角边角”定理. 2．能运用“角边角”定理解决简单的推理证明 问题.
问题1　先任意画出一个△ABC，再画一个△A′B′C′，使A′B′ =AB，∠A′=∠A，∠B′=∠B（即两角和它们的夹边分别相等）．把画好的△A′B′C′剪下来，放到△ABC 上，它们全等吗？
探究“ASA”判定方法
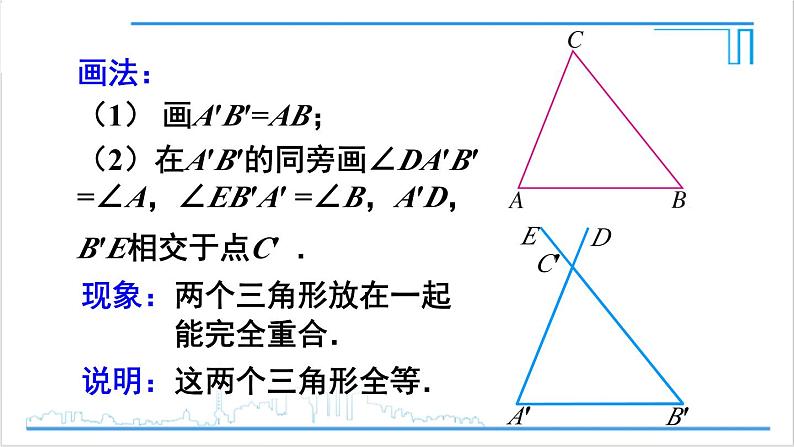
现象：两个三角形放在一起 能完全重合．说明：这两个三角形全等．
画法：（1） 画A′B′=AB；（2）在A′B′的同旁画∠DA′B′ =∠A，∠EB′A′ =∠B，A′D，B′E相交于点C′ ．
几何语言：在△ABC 和△ A′B′ C′ 中，
∴△ABC ≌△ A′B′ C′（ASA）．
　　归纳概括“ASA”判定方法:两角和它们的夹边分别相等的两个三角形全等（简写为“角边角”或“ASA”）．
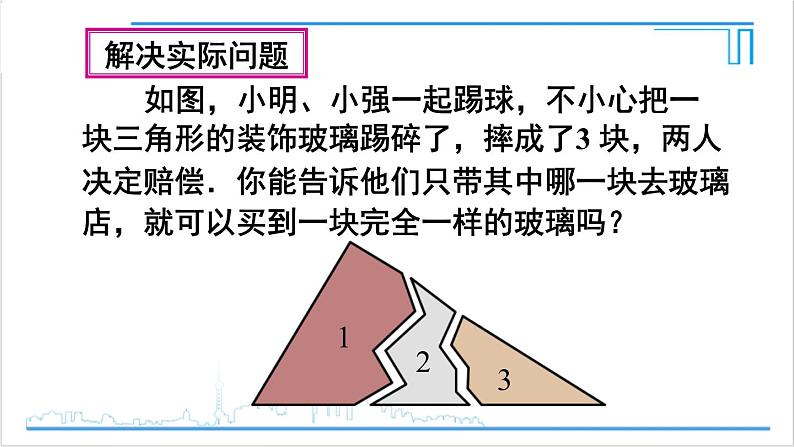
如图，小明、小强一起踢球，不小心把一 块三角形的装饰玻璃踢碎了，摔成了3 块，两人决定赔偿．你能告诉他们只带其中哪一块去玻璃店，就可以买到一块完全一样的玻璃吗？
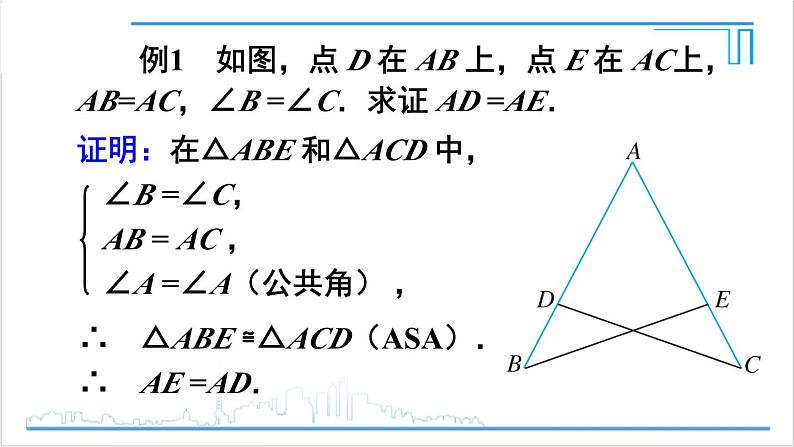
证明：在△ABE 和△ACD 中，
∴　△ABE ≌△ACD（ASA）．∴　AE =AD．
　　例1　如图，点 D 在 AB 上，点 E 在 AC上，AB=AC，∠B =∠C．求证 AD =AE．
　　例2　如图，在△ABC 和△DEF 中，∠A =∠D，∠B =∠E，BC =EF . 求证△ABC ≌△DEF.
探究“AAS”判定方法
证明：在△ABC 中， ∠A +∠B +∠C =180°，∴∠C = 180°-∠A-∠B.同理∠F =180°-∠D -∠E.又 ∠A =∠D， ∠B =∠E，∴∠C = ∠F .在△ABC 和△DEF 中，
∴△ABC ≌△DEF（ASA）．
　　归纳概括“AAS”判定方法:两角分别相等且其中一组等角的对边相等的两个三角形全等（简写为“角角边”或“AAS”）．
也就是说，三角形的两个角的大小和其中一个角的对边的长度确定了，这个三角形的形状、大小就确定了.
证明：∵　∠DAB =∠EAC， ∴　∠DAC =∠EAB. ∵　AE⊥BE，AD⊥DC， ∴　∠D =∠E =90°. 在△ADC 和△AEB 中，
问题2　如图，AE⊥BE，AD⊥DC，CD =BE，∠DAB =∠EAC．求证：AB =AC．
∴　△ADC ≌△AEB（AAS）．∴　AB =AC．
问题3　如图，E，F 在线段AC上，AD∥CB，AE = CF．若∠B =∠D，求证：DF =BE．
证明：∵　AD∥CB ， ∴　∠A =∠C. ∵　AE =CF ， ∴　AF =CE.在△ADF 和△CBE 中,
问题3 如图，E，F 在线段AC上，AD∥CB，AE = CF．若∠B =∠D，求证：DF =BE．
∴　△ADF ≌△CBE（AAS）．∴　DF =BE．
变式　若将条件 “∠B =∠D”变为“DF∥BE”，那么原结论还成立吗？若成立，请证明；若不成立，请说明理由．
练习1 如图，EA⊥AB，DB⊥AB，∠ACE =∠BDC，AE =BC，试判断CE与CD的关系.
∴△ACE ≌△BDC（AAS）．
解：∵EA⊥AB，DB⊥AB，∴∠A =∠B =90°，在△ACE和△BDC中，
练习2 判断.a.有两条边和一个角对应相等的两个三角形全等. （ ）b.有两个角和一条边对应相等的两个三角形全等. （ ）
1.如图，已知AB = DC，AD = BC，E、F是DB上的两点且BF = DE.若∠AEB = 120°，∠ADB = 30°，则∠BCF =（ ）A.150°B.40°C.80°D.90°
2. 如图，AB⊥BC，AD⊥DC，垂足分别为B，D，∠1=∠2. 求证AB=AD.
【课本P41 练习 第1题】
【课本P41 练习 第2题】
3.如图，要测量池塘两岸相对的两点A，B的距离，可以在池塘外取AB的垂线BF上的两点C，D，使BC=CD，再画出BF的垂线DE，使E与A， C在一条直线上，这时测得DE的长就是AB的长. 为什么？
4.已知：如图，∠ABC = ∠DEF，AB = DE，要证明△ABC≌△DEF，（1）若以“SAS”为依据，还须添加的一个条件为____________.（2）若以“ASA”为依据，还须添加的一个条件为_____________.（3）若以“AAS”为依据，还须添加的一个条件为_____________.
5.如图，点 E、F 在BD上，且 AB = CD，BF = DE，AE = CF，求证：AC 与 BD 互相平分.
证明：∵BF = DE，∴BF－EF = DE－EF，即BE = DF.在△ABE和△CDF中，
∴△ABE≌△CDF. ∴∠B =∠D.∴AB∥CD. ∴∠BAO =∠DCO.在△ABO和△CDO中，∴△ABO≌△CDO，∴BO = DO，AO = CO，即AC与BD互相平分.
两角和它们的夹边分别相等的两个三角形全等（简称为“角边角”或“ASA”）．
两角分别相等且其中一组等角的对边相等的两个三角形全等（简称为“角角边”或“AAS”）．