人教版（2024）八年级上册12.2 三角形全等的判定优质ppt课件

这是一份人教版（2024）八年级上册12.2 三角形全等的判定优质ppt课件，共27页。PPT课件主要包含了知识点1，知识点2，ADBC，ACBD，AAS，基础巩固，综合应用，拓展延伸等内容，欢迎下载使用。
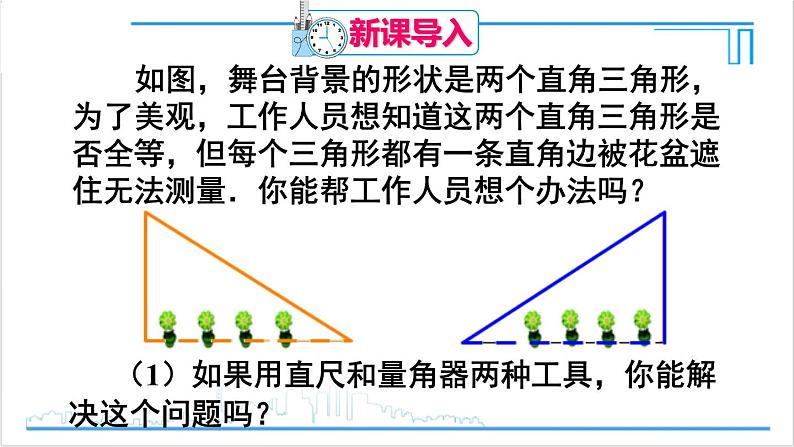
如图，舞台背景的形状是两个直角三角形， 为了美观，工作人员想知道这两个直角三角形是否全等，但每个三角形都有一条直角边被花盆遮住无法测量．你能帮工作人员想个办法吗？
　 （1）如果用直尺和量角器两种工具，你能解决这个问题吗？
　 （2）如果只用直尺，你能解决这个问题吗？
学习目标： 1．探究直角三角形全等的判定方法. 2．能运用三角形全等的判定方法判断两个直角 三角形全等.
任意画一个Rt△ABC，使∠C =90°. 再画一个Rt△A′B′C′，使∠C′=90°，B′C′=BC，A′B′=AB .然后把画好的Rt△A′B′C′剪下来放到Rt△ABC上，你发现了什么？
探索“HL”判定方法
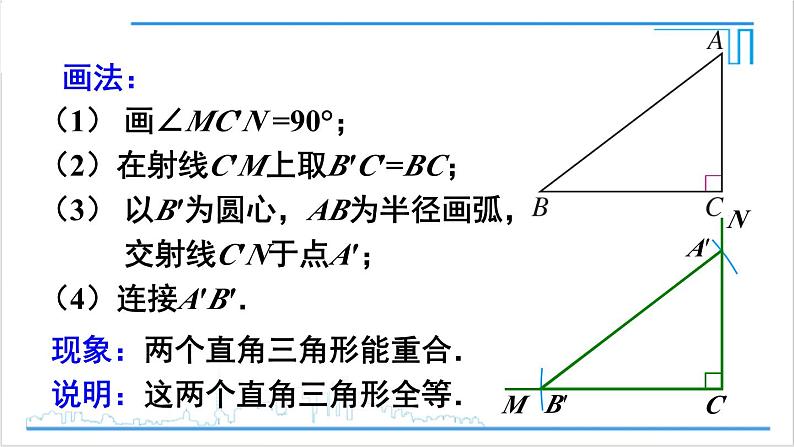
（1） 画∠MC′N =90°；（2）在射线C′M上取B′C′=BC；（3） 以B′为圆心，AB为半径画弧， 交射线C′N于点A′；（4）连接A′B′．
现象：两个直角三角形能重合．说明：这两个直角三角形全等．
归纳概括“HL”判定方法
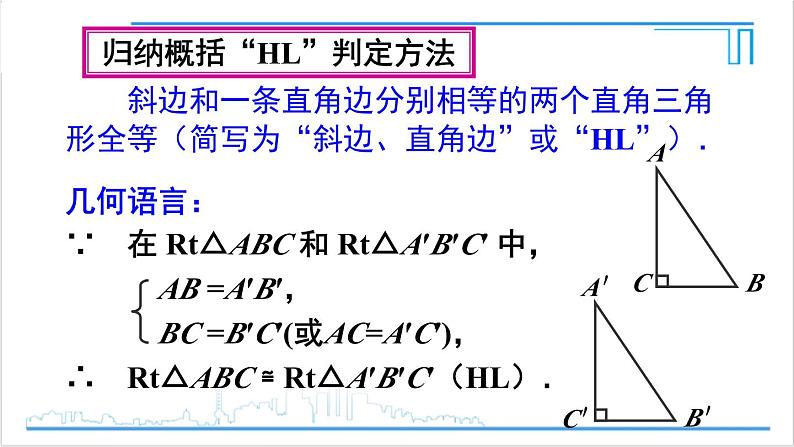
　　斜边和一条直角边分别相等的两个直角三角形全等（简写为“斜边、直角边”或“HL”）．
几何语言：∵　在 Rt△ABC 和 Rt△A′B′C′ 中， 　 AB =A′B′， BC =B′C′(或AC=A′C′)，∴　Rt△ABC ≌ Rt△A′B′C′（HL）．
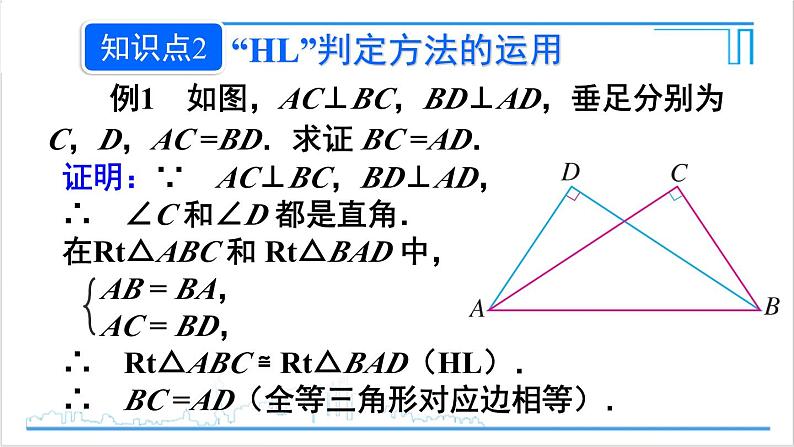
证明：∵　AC⊥BC，BD⊥AD，∴　∠C 和∠D 都是直角．在Rt△ABC 和 Rt△BAD 中， AB = BA， AC = BD，∴　Rt△ABC ≌ Rt△BAD（HL）．∴　BC =AD（全等三角形对应边相等）．
例1　如图，AC⊥BC，BD⊥AD，垂足分别为C，D，AC =BD．求证 BC =AD．
“HL”判定方法的运用
变式1　如图，AC⊥BC，BD⊥AD，要明证△ABC ≌△BAD，需要添加一个什么条件？请说明理由．（1） （ ）；（2） （ ）；（3） （ ）；（4） （ ）．
∠DAB = ∠CBA
∠DBA = ∠CAB
例2　如图，有两个长度相同的滑梯，左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等，两个滑梯的倾斜角∠ABC 和∠DFE 的大小有什么关系？为什么？
∠ABC +∠DFE = 90°
证明：∵AC⊥AB，DE⊥DF，∴∠CAB =∠FDE =90°．在Rt△ABC 和 Rt△DEF 中，
∴Rt△ABC ≌ Rt△DEF（HL）．　　　
证明：∴∠ABC =∠DEF （全等三角形对应角相等）．∵ ∠DEF +∠DFE =90°， ∴ ∠ABC +∠DFE =90°．
　　练习1　如图，C 是路段AB 的中点，两人从C 同时出发，以相同的速度分别沿两条直线行走，并同时到达D，E 两地．DA⊥AB，EB⊥AB．D，E 与路段AB的距离相等吗？为什么？
【课本P43 练习 第1题】
解：D、E与路段AB的距离相等.理由：∵C是路段AB的中点，∴AC = BC，又∵两人同时同速度出发，并同时到达D，E两地.∴CD = CE，
又DA⊥AB，EB⊥AB，∴∠A=∠B =90°，在Rt△ACD与Rt△BCE中，∴Rt△ACD≌Rt△BCE（HL).∴DA = EB，即D、E与路段AB的距离相等.
练习2　如图，AB = CD，AE⊥BC，DF⊥BC，垂足分别为E，F，CE = BF．求证：AE = DF．
【课本P43 练习 第2题】
证明：∵CE = BF，∴CE - EF = BF–EF，即CF = BE.又∵AE⊥BC，DF⊥BC，∴∠DFC =∠AEB =90°.
在Rt△DFC与Rt△AEB中，∴Rt△DFC≌Rt△AEB（HL).∴AE = DF.
练习3　如图，B、E、F、C 在同一直线上，AF⊥BC 于F，DE⊥BC与E，AB = DC，BE = CF，你认为 AB 平行于 CD 吗？说说你的理由.
解：平行.理由：∵AF⊥BC，DE⊥BC，∴∠AFB 和∠DEC 都是直角，又 BE = CF，∴BE+EF=CF+EF，即 BF = CE.
在 Rt△ABF 和 Rt△DCE 中，AB=CD，BF=CE，∴Rt△ABF≌Rt△DCE(HL)，∴∠B =∠C，AB∥CD.
1. 在 Rt△ABC 和 Rt△A′B′C′ 中，∠C′=∠C=90°，∠B′=∠A，AB = B′A′，则下列结论正确的是（ ）A.AC = A′C′B.BC = B′C′C.AC = B′C′D.∠A′=∠A
2.如图，∠DCE = 90°，CD = CE，AD⊥AC，BE⊥AC，垂足分别为A、B，试说明AD + AB = BE.
解：∵AD⊥AC，BE⊥AC，∴∠A =∠CBE =90°，∴∠D +∠ACD =90°.又∵∠DCE = 90°，∴∠ACD +∠BCE = 90°，∴∠D =∠BCE.
在△ACD和△BEC中，∴△ACD≌△BEC(AAS).∴AD = BC，AC = BE，∴AD+AB = BC+AB = AC = BE.
3.如图，在△ABC中，∠BAC = 90°，AB=AC，EF是过点A的直线，BE⊥EF于E，CF⊥EF于F，试探求线段BE、CF、EF之间的关系，并加以证明.
解：BE + CF = EF，证明如下：∵BE⊥EF，CF⊥EF，∴∠BEA =∠AFC =90°.又∠BAC = 90°，∴∠EAB +∠CAF =180°-∠BAC = 90°，
∴∠EAB =∠FCA，在△ABE和△CAF中，∴△ABE≌△CAF(AAS).∴BE = AF，AE = CF，∴BE+CF = AF+AE = EF.