初中数学人教版（2024）八年级上册13.3.1 等腰三角形优秀课件ppt

这是一份初中数学人教版（2024）八年级上册13.3.1 等腰三角形优秀课件ppt，共23页。PPT课件主要包含了新课导入，导入课题，学习目标，推进新课，知识点1，巩固练习，知识点2，等腰三角形性质的运用，随堂演练，基础巩固等内容，欢迎下载使用。

在前面学习轴对称图形中，大家知道等腰三角形是轴对称图形，今天我们就运用轴对称图形的性质来探究等腰三角形的性质.
（1）知道等腰三角形的性质.
（2）能运用等腰三角形的性质进行证明和计算.
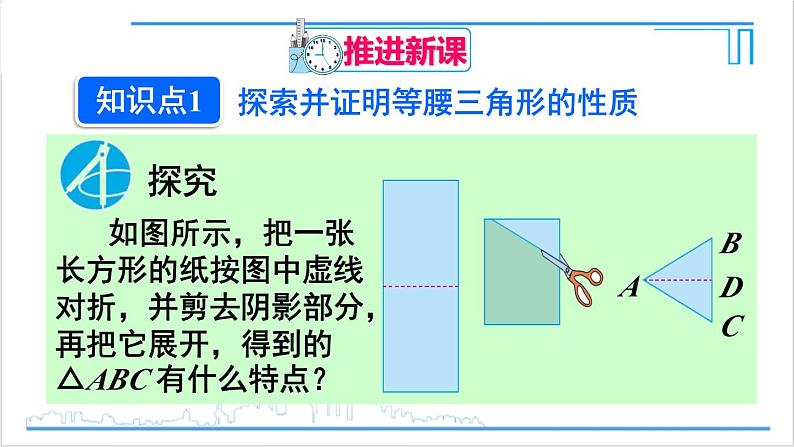
探索并证明等腰三角形的性质
　　如图所示，把一张长方形的纸按图中虚线对折，并剪去阴影部分，再把它展开，得到的△ABC 有什么特点？
　　仔细观察自己剪出的等腰三角形纸片，你能发现这个等腰三角形的特征吗？
　　同学们剪下的等腰三角形纸片大小不同，形状各异，是否都具有上述所概括的特征？
　　在练习本上任意画一个等腰三角形，把它剪下来，折一折，上面得出的结论仍然成立吗？由此你能概括出等腰三角形的性质吗？
　　 等腰三角形的性质:性质1：等腰三角形的两个底角相等；性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．
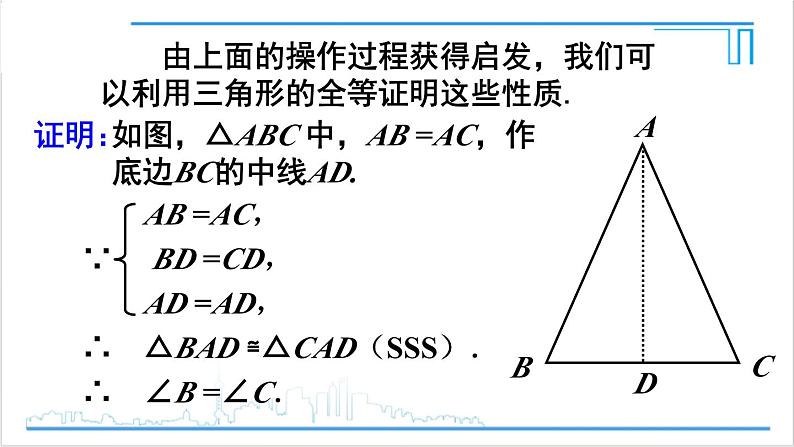
由上面的操作过程获得启发，我们可以利用三角形的全等证明这些性质.
如图，△ABC 中，AB =AC，作底边BC的中线AD.
　AB =AC，∵ 　BD =CD，　 AD =AD，∴　△BAD ≌△CAD（SSS）．∴　∠B =∠C．
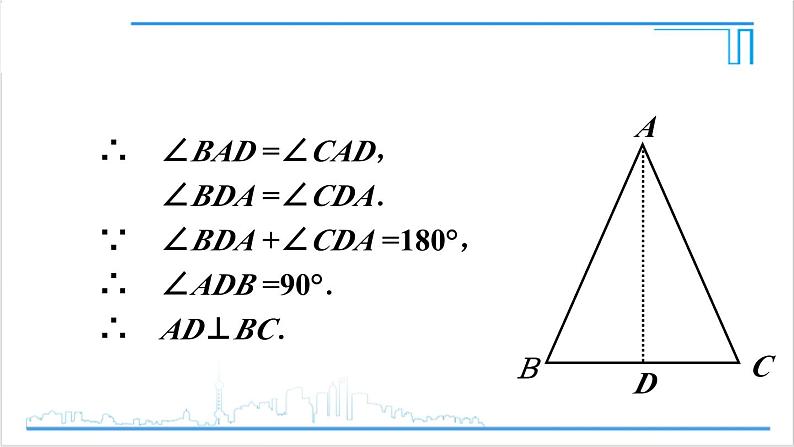
∴　∠BAD =∠CAD， ∠BDA =∠CDA．∵　∠BDA +∠CDA =180°，∴　∠ADB =90°．∴　AD⊥BC．
　　在等腰三角形性质的探索过程和证明过程中“折痕”“辅助线”发挥了非常重要的作用，由此，你能发现等腰三角形具有什么特征？ 等腰三角形是轴对称图形，底边上的中线（顶角平分线、底边上的高）所在直线就是它的对称轴．
　　练习1　填空：（1）如图，△ABC 中，AB =AC， ∠A =36°, 则∠B = °；
　　（2）如图，△ABC 中， AB =AC，∠B = 36°， 则∠A = °；
例1 如图，在△ABC 中，AB =AC，点D 在AC 上，且BD =BC =AD．求△ABC 各角的度数．
解： ∵ AB =AC，BD=BC=AD，∠ABC=∠C=∠BDC，∠A= ∠ABD设∠A=x，则∠BDC= ∠A+∠ABD=2x，从而∠ABC= ∠C= ∠BDC=2x，
于是在△ABC 中，有∠A +∠ABC+ ∠C = x+2x+2x = 180°解得x = 36°.所以，在△ABC 中，∠A = 36°，∠ABC =∠C =72°.
练习2 在下列等腰三角形中，分别求出它们的底角的度数.
【课本P77 练习 第1题】
1.等腰△ABC中，AB=AC，∠A=30°，则∠B=（ ）
A．30° B．60° C．75° D．85°
2.等腰三角形的一个外角是100°，它的顶角的度数是（ ）
A．80°B．20°C．20°或80°D．50°或80°
【课本P77 练习 第2题】
3. 如图，△ABC是等腰直角三角形（AB=AC，∠BAC=90°）， AD是底边BC上的高. 标出∠B，∠C，∠BAD，∠DAC的度数，并写出图中所有相等的线段.
【课本P77 练习 第3题】
4.如图，在△ABC中，AB=AD=DC，∠BAD=26°.求∠B和∠C的度数.
3. 如图，在△ABC中，AD平分∠BAC，AD=AC=BD，求∠B的度数.
解：∵AD平分∠BAC，∴∠BAD=∠CAD.∵AD=AC，∴∠ADC=∠C.∵AD=BD，∴∠BAD=∠B.设∠B=x，则∠BAC=2∠BAD=2x，∠C=∠ADC=∠B+∠BAD=2x，∴∠B+∠BAC+∠C=x+2x+2x=180°，解得x=36°，∴∠B=36°.
4.如图，在△ABC中，AB＝AC，E在CA的延长线上，∠AEF＝∠AFE，求证：EF⊥ BC.
证明：作AD⊥BC，垂足为D.∵AB=AC，∴∠BAC=2∠CAD.∵∠AEF=∠AFE，∴∠BAC=∠AEF+∠AFE=2∠AEF.∴∠CAD=∠AEF，∴AD∥EF.∵AD⊥BC，∴EF⊥BC.
　　 等腰三角形的性质:性质1：等腰三角形的两个底角相等；性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合．