高教版（2021）拓展模块一 上册第1章 充要条件1.1 充分条件和必要条件公开课教学设计

这是一份高教版（2021）拓展模块一 上册第1章 充要条件1.1 充分条件和必要条件公开课教学设计，共6页。教案主要包含了设计意图等内容，欢迎下载使用。

学习重难点
教材分析
充分条件和必要条件的概念是中学数学中最重要的数学概念之一，为今后的数学学习特别是数学推理的学习打下基础，本节先学习充分条件和必要条件，下一节再学习充要条件，适当降低了难度.
学情分析
学生在学习有充分条件和必要条件这一概念时知识储备不够丰富，逻辑思维能力的训练不够充分，这为教师教学带来一定困难，这就要求教师不要一步到位，而要逐步深化知识．
教学工具
教学课件
课时安排
1课时
教学过程
（一）创设情境，生成问题
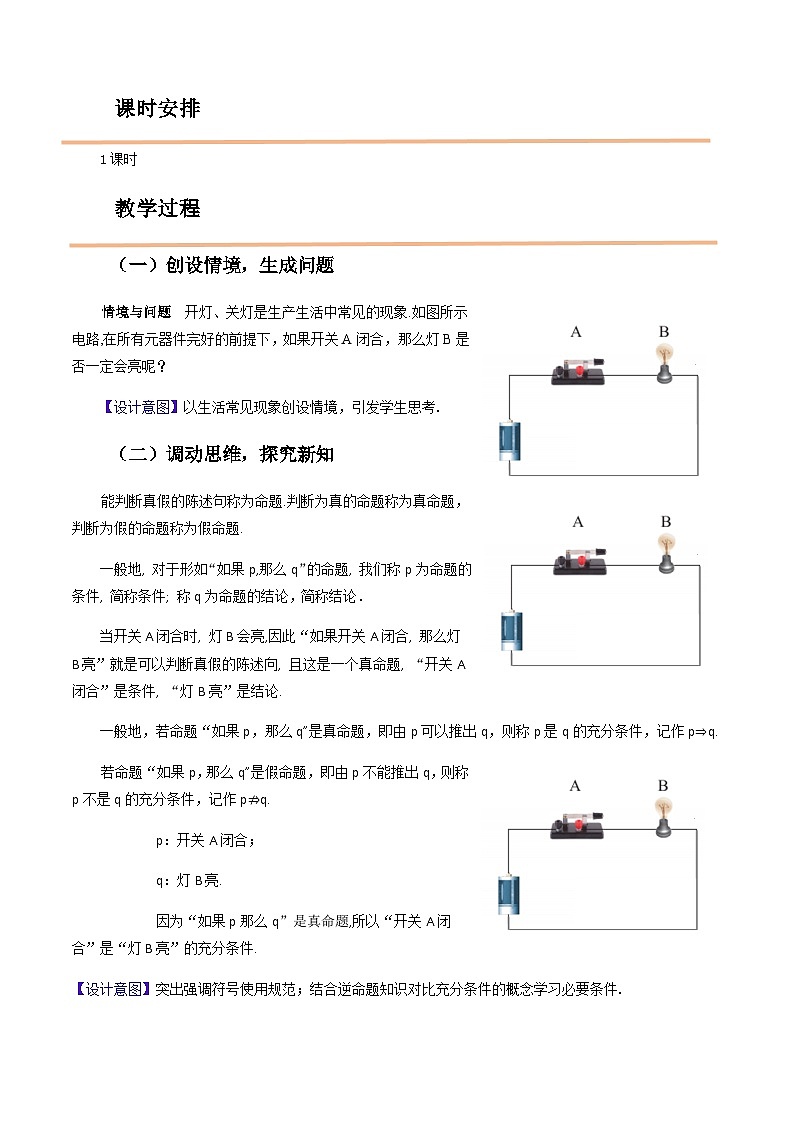
情境与问题 开灯、关灯是生产生活中常见的现象.如图所示电路,在所有元器件完好的前提下，如果开关A闭合，那么灯B是否一定会亮呢？
【设计意图】以生活常见现象创设情境，引发学生思考.
（二）调动思维，探究新知
能判断真假的陈述句称为命题.判断为真的命题称为真命题，判断为假的命题称为假命题.
一般地, 对于形如“如果p,那么q”的命题, 我们称p为命题的条件, 简称条件; 称q为命题的结论，简称结论．
当开关A 闭合时, 灯B 会亮,因此“如果开关A 闭合, 那么灯B 亮”就是可以判断真假的陈述向, 且这是一个真命题, “开关A闭合”是条件, “灯B亮”是结论.
一般地，若命题“如果p，那么q”是真命题，即由p可以推出q，则称p是q的充分条件，记作p⇒q.
若命题“如果p，那么q”是假命题，即由p不能推出q，则称p不是q的充分条件，记作p⇏q.
p：开关A 闭合；
q：灯B 亮.
因为“如果p那么q”是真命题,所以“开关A闭合”是“灯B亮”的充分条件.
【设计意图】突出强调符号使用规范；结合逆命题知识对比充分条件的概念学习必要条件.
（三）巩固知识，典例练习
【典例1】指出下列命题的条件p和结论q，并判断p是否为q的充分条件.
(1)如果x是整数，那么x是有理数；
(2)如果a=0，那么ab=0；
(3)第一象限角都是锐角.
解 (1)条件p:x是整数;结论q: 是有理数.因为当x 是整数时, x一定是有理数，所以此命题是真命题，p是q的充分条件；
（2）条件P: a=0，q: 那么ab=0.因为当a=0时，一定有ab=0，所以此命题是真命题，p是q的充分条件.
(3) 原命题可以表述为：“如果一个角是第一象限角,那么这个角是锐角”，条件p: 一个角是第一象限角, q: 这个角是锐角. 因为第一象限角构成的集合为, 其中的角不一定是锐角, 所以此命题是假命题，p不是q的充分条件
情境与问题：如果“灯B亮”，那么是否一定需要“开关A闭合”呢？
将命题“如果p，那么q”中的条件p和结论q互换，变成“如果q，那么p”，称这个命题为原命题的逆命题.
命题“如果开关A闭合，那么灯B亮”的逆命题为“如果灯B亮，那么开关A闭合”.
命题“如果开关A闭合，那么灯B亮”的逆命题为“如果灯B亮，那么开关A闭合”.
一般地，若命题“如果p，那么q”的逆命题“如果q，那么p”是真命题，则称p是q的必要条件，记作p⇐q.
若命题“如果p，那么q”的逆命题“如果q，那么p”是假命题，则称p不是q的必要条件，记作p⇍q.
命题“如果灯B亮，那么开关A闭合”是真命题,所以“开关A闭合”是“灯B亮”的必要条件，即如果“灯B亮”，一定需要“开关A闭合”.
【典例2】判断下列命题中的条件p是否为结论q的必要条件.
(1)如果x+y为偶数，那么x、y都是偶数；
（2）如果，那么；
（3）如果a=b，那么|a|=|b|
解 （1）因为“如果x+y为偶数，那么x、y都是偶数”的逆命题“如果x、y都是偶数，那么x+y为偶数”是真命题，所以如果x+y为偶数是x、y都是偶数必要条件.
（2）因为“如果，那么”的逆命题“如果，那么” 是假命题，所以如果不是必要条件.
（3）因为“a=b，那么|a|=|b|”的逆命题“如果|a|=|b|，那么a=b” 是假命题，所以如果a=b不是|a|=|b|必要条件.
【设计意图】直接利用必要条件概念通过判断逆命题真假判断原命题的条件与结论关系，
（四）巩固练习，提升素养
1．指出下列命题的条件p和结论q，并判断p是否为q的充分条件．
（1）如果x>2,那么|x|>2.
（2）如果,那么α是第一象限角.
（3）如果指数函数的底数a>1，那么这个指数函数在R上是增函数.
（4）两个三角形的面积相等.
2.指出下列命题的条件p和结论q，并判断p是否为q的必要条件.
(1)如果a+2>b+1，那么a>b.
(2)如果一次函数是R上的增函数，那么k>0.
(3)如果那么
（4）如果直线经过第二三四象限，那么k