高教版（2021）拓展模块一 上册2.2.3 向量的数乘运算精品ppt课件

这是一份高教版（2021）拓展模块一 上册2.2.3 向量的数乘运算精品ppt课件，共22页。PPT课件主要包含了调动思维探究新知，学习目标，创设情境生成问题，典例1计算，巩固知识典例练习，巩固练习提升素养，课堂小结，作业布置等内容，欢迎下载使用。

向量a−b称为向量a与b的差.求两个向量差的运算称为向量的减法，也称a−b为差向量．
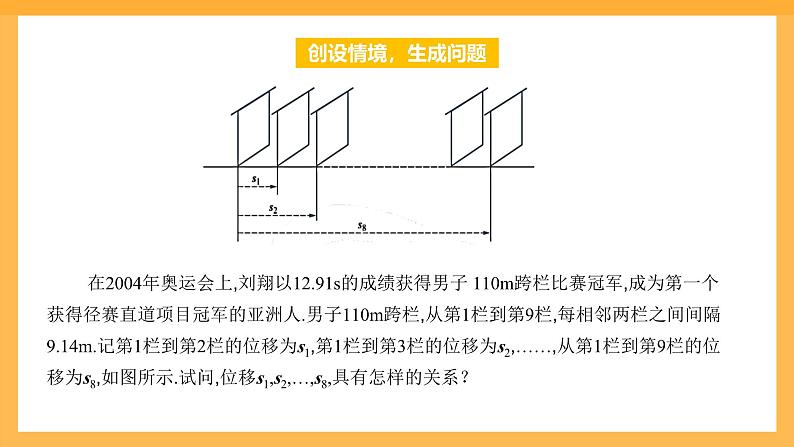
在2004年奥运会上,刘翔以12.91s的成绩获得男子 110m跨栏比赛冠军,成为第一个获得径赛直道项目冠军的亚洲人.男子110m跨栏,从第1栏到第9栏,每相邻两栏之间间隔9.14m.记第1栏到第2栏的位移为s1,第1栏到第3栏的位移为s2,……,从第1栏到第9栏的位移为s8,如图所示.试问,位移s1,s2,…,s8,具有怎样的关系？
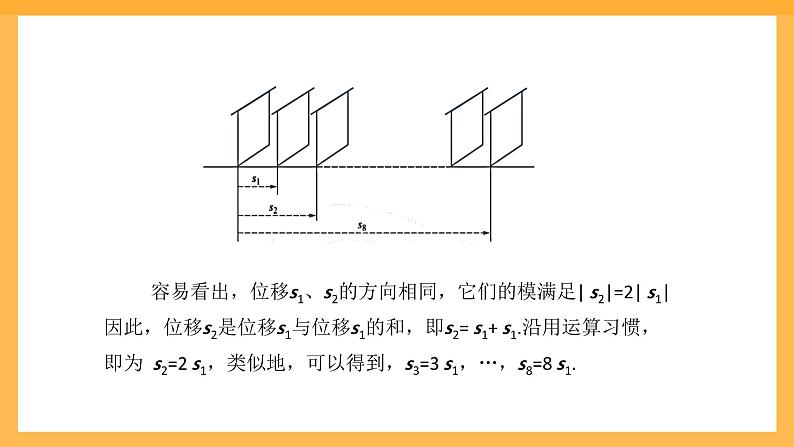
容易看出，位移s1、s2的方向相同，它们的模满足| s2|=2| s1|因此，位移s2是位移s1与位移s1的和，即s2= s1+ s1.沿用运算习惯，即为 s2=2 s1，类似地，可以得到，s3=3 s1，…，s8=8 s1.
一般地，实数λ与向量a的乘积仍是一个向量,记作λa. λa的模为|λa|= |λ||a|. 当λ>0时, λa的方向与a的方向相同； 当λ<0时, λa的方向与a的方向相反； 当λ=0时,因为 λa=0,所以其方向是任意的.
上述定义表明,当 λ>0时,向量λa可以看作由向量a伸长或缩短λ倍得到；当 λ<0时,向量 λa可以看作由向量−a 伸长或缩短|λ|倍得到. 这是向量数乘运算的几何意义．
求一个数λ与向量a的乘法运算称为数与向量的乘法运算,简称数乘运算.
容易验证,对于任意向量a、b及任意实数 λ、μ,向量的数乘运算满足以下法则:
(λμ) a=λ(μa)= μ (λa)(λ+μ) a=λa +μaλ(a+b)= λa+λb
可以看出,向量λa与向量a平行.反之,若有一个向量b与向量a(a≠0)平行,则向量b与a的关系如下：
一般地，若向量c=λa+μb(λ、μ均为实数),则称向量c可以由向量a、b线性表示.
6．已知向量i、j分别为轴上的单位向量，试判断下列向量a、b是否共线
(1) 读书部分： 教材章节2.2.3； (2) 书面作业： P32习题2.2的5,6,7.