中职数学高教版（2021）拓展模块一 上册4.4.2 二面角精品课件ppt

这是一份中职数学高教版（2021）拓展模块一 上册4.4.2 二面角精品课件ppt，共19页。PPT课件主要包含了学习目标，创设情境生成问题，调动思维探究新知，巩固知识典型练习，巩固知识典例练习，巩固练习提升素养，课堂小结，作业布置等内容，欢迎下载使用。
打开笔记本计算机时,显示屏的开合程度不同,键盘与屏幕所在平面的相对位置就不同,如图所示.怎样来描述这种不同呢？
观察可知,显示屏的开合程度可以用角度来描述.
  平面内的一条直线把这个平面分成两部分,其中的每一部分都称为半平面. 从一条直线出发的两个半平面所组成的图形称为二面角,这条直线称为二面角的棱,这两个半平面称为二面角的面.
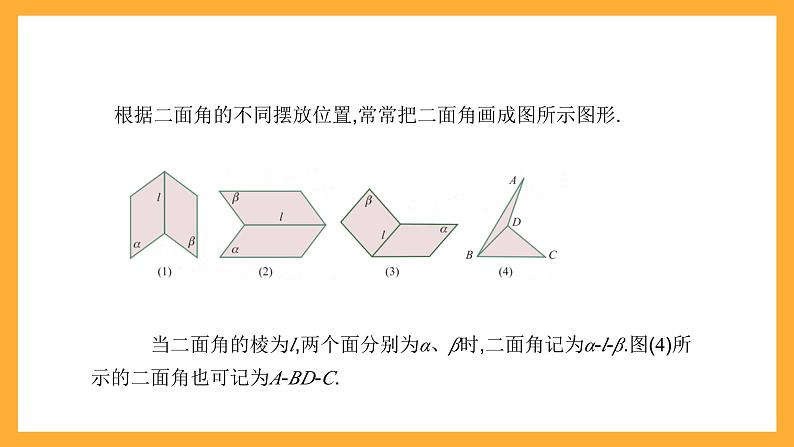
根据二面角的不同摆放位置,常常把二面角画成图所示图形.
当二面角的棱为l,两个面分别为α、β时,二面角记为α-l-β.图(4)所示的二面角也可记为A-BD-C. 
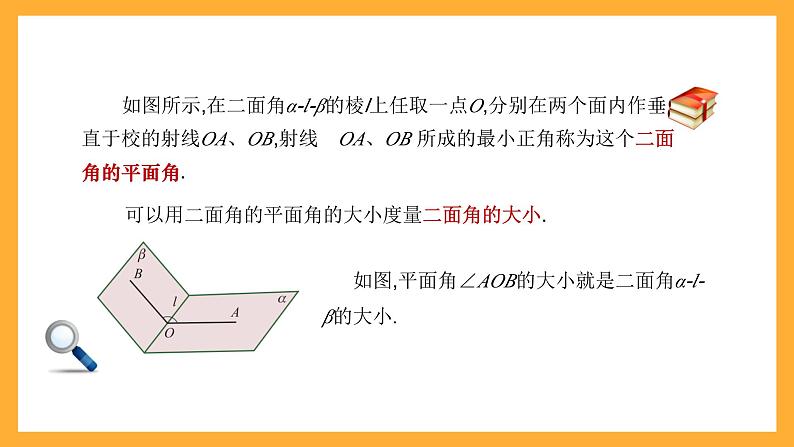
如图,平面角∠AOB的大小就是二面角α-l-β的大小.
  如图所示,在二面角α-l-β的棱l上任取一点O,分别在两个面内作垂直于校的射线OA、OB,射线 OA、OB 所成的最小正角称为这个二面角的平面角. 
可以用二面角的平面角的大小度量二面角的大小.
规定,当二面角的两个半平面重合时,二面角为零角;当二面角的两个半平面构成一个面时,二面角为平角.于是,二面角的取值范围是[0,π].当二面角的平面角为直角时,称为直二面角.
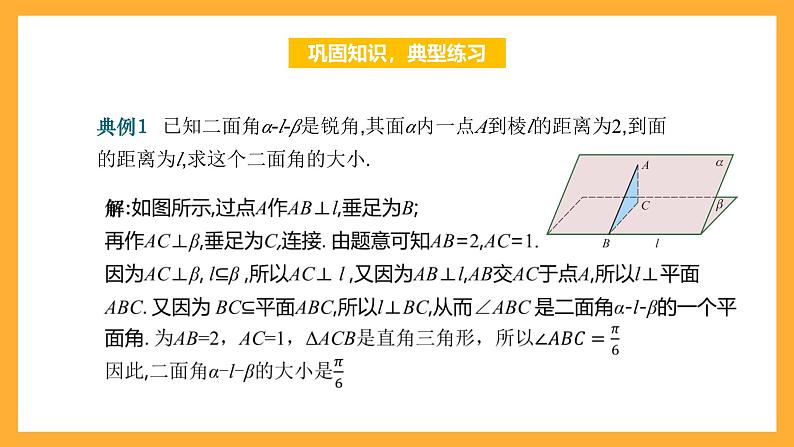
典例1  已知二面角α-l-β是锐角,其面α内一点A到棱l的距离为2,到面的距离为l,求这个二面角的大小.
典例2 求证:如果一个平面γ垂直于二面角α-l-β的棱l,O为垂 足,且与两半平面的交线分别为 OA、OB,如图所示.那么∠AOB 是二面角α-l-β的平面角 . 
证明:因为γ∩α=OA,γ∩α=OB,所以OA ⊆ γ,OB ⊆ γ.  又因为l⊥γ ,所以l⊥OA,l⊥OB. 因此,∠AOB 是二面角α-l-β的一个平面角.
例4中,垂直于棱l的平面,与二面角α-l-β的交线 OA、OB构成了二面角的平面角∠AOB,这又为我们提供了一种寻找二面角的平面角的方法.
我们己经知道了两条直线所成的角和直线与平面所成的角的定义,那么,两个平面所成的角怎样定义呢？
典例3 如图所示,在正方体ABCD-A1B1C1D1中,平面 AB1C1D与平面ABCD 所成的角的大小.  
1. 己知二面角α-l-β,C∈α ,D∈β,AC⊥AB,AD⊥AB,垂足均为A,则二面角α-AB-β的平面角是 . 2. 已知正方体 ABCD-A1B1C1D1,试找出二面角A1-BD-A 与二面角A1-BD-C 的一个平面角,并分析二者之间的大小关系. 
6. 我国水利建设具有悠久的历史,尤其中华人民共和国成立后,修建了许多水车,在防洪、用水、供电、灌溉等方面发挥了巨大作用.如图所示,某水库大坝高85m,斜坡面与水平面成45°角,则斜坡面有多长？
(1) 读书部分： 教材章节4.4.2； (2) 书面作业： P144习题4.4的3.
数学是一种别具匠心的艺术