高教版（2021）拓展模块一 上册5.1.1 复数的概念完整版ppt课件

这是一份高教版（2021）拓展模块一 上册5.1.1 复数的概念完整版ppt课件，共18页。PPT课件主要包含了学习目标，创设情境生成问题，调动思维探究新知，巩固知识典例练习，温馨提示，巩固练习提升素养，课堂小结，作业布置等内容，欢迎下载使用。

很久以前,人们认为一元二次方程x²+1=0 是无解的.但是,随着对数系的深人研究,人们逐渐意识到应该存在一个数,它就是该方程的解.
  依照引入负数,使方程x+1=0有解的方法,是否可以引入一个数使方程x²+1=0有解呢？
假设有一个数是方程x²+1=0的解,那么这个数的平方应该等于-1. 这个数不在实数集内. 为此,人们引人了一个新的数,记作i,称为虚数单位. 
既然i是一个数,那么它与实数就可以进行运算.实数b与i的乘积写成 bi,实数a与bi的和写成a+bi. 
把形如a+bi (a、b∈R)的数称为复数,其中a称为复数的实部, b称为复数的虚部. 
复数通常用小写英文字母z、w……表示,如z=a+bi.全体复数构成的集合称为复数集,用C表示,即C={z|z= a+bi,a,b∈R}. 
当b=0时,复数a+bi就是实数; 当b≠0时,复数a+bi称为虚数; 当a=0且b≠0时,复数称为纯虚数.
全体虚数构成的集合称为虚数集,全体纯虚数构成的集合称为纯虚数集,它们与实数集、复数集之间具有怎样的关系？
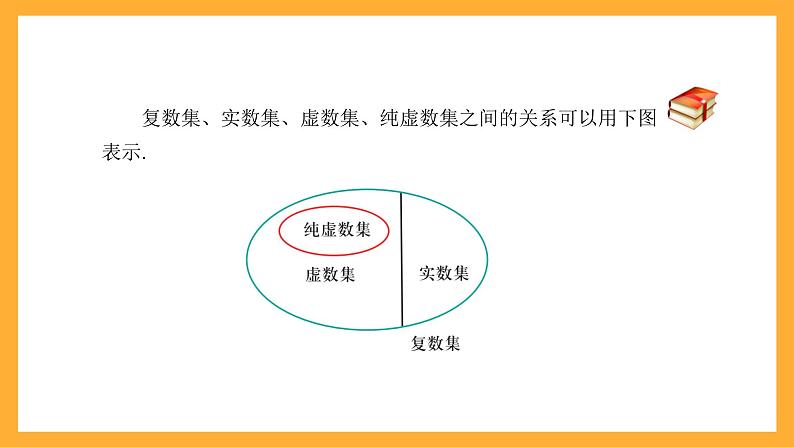
复数集、实数集、虚数集、纯虚数集之间的关系可以用下图表示.
典例1  指出下列复数的实部和虚部,并判断这些复数是实数还是虚数.若是虚数,判断其是否为纯虚数. （1）2；（2）3-i；（3）5i；
解：（1）复数2的实部是2,虚部是0,它是实数； （2）复数 3-i的实部是3,虚部是-1,它是虚数,不是纯虚数； （3）复数5i 的实部是 0,虚部是5,它是虚数,而且是纯虚数. 
如果两个复数a+bi与c+di的实部与虚部分别相等,就称这两个复数相等，记作 a+bi=c+di. 即,如果a、b、c、d都是实数,那么 a+bi=c+di⇔ a=c且b=d. 特别地, a+bi=0 ⇔ a=0且b=0.
从两个复数相等的定义可知,复数a+bi与有序实数对(a,b)之间是一一对应的.
典例2 求满足下列条件的实数a和b. （1）(a+2b)-i=6a+(a-b)i； （2）(a+b+1)+(a-b+2)i=0.
已知a是实数，i是虚数单位，若z＝a2－1＋(a＋1)i是纯虚数，则a＝__1__.
[解析]　∵z＝a2－1＋(a＋1)i是纯虚数，∴ ，解得a＝1.故答案为1．
(1) 读书部分： 教材章节5.1.1； (2) 书面作业： P162习题5.1的1,2,3.
没有大胆的猜测就做不出伟大的发现