高考数学科学创新复习方案提升版素能培优（三）利用导数研究函数的性质学案（Word版附解析）

这是一份高考数学科学创新复习方案提升版素能培优（三）利用导数研究函数的性质学案（Word版附解析），共7页。

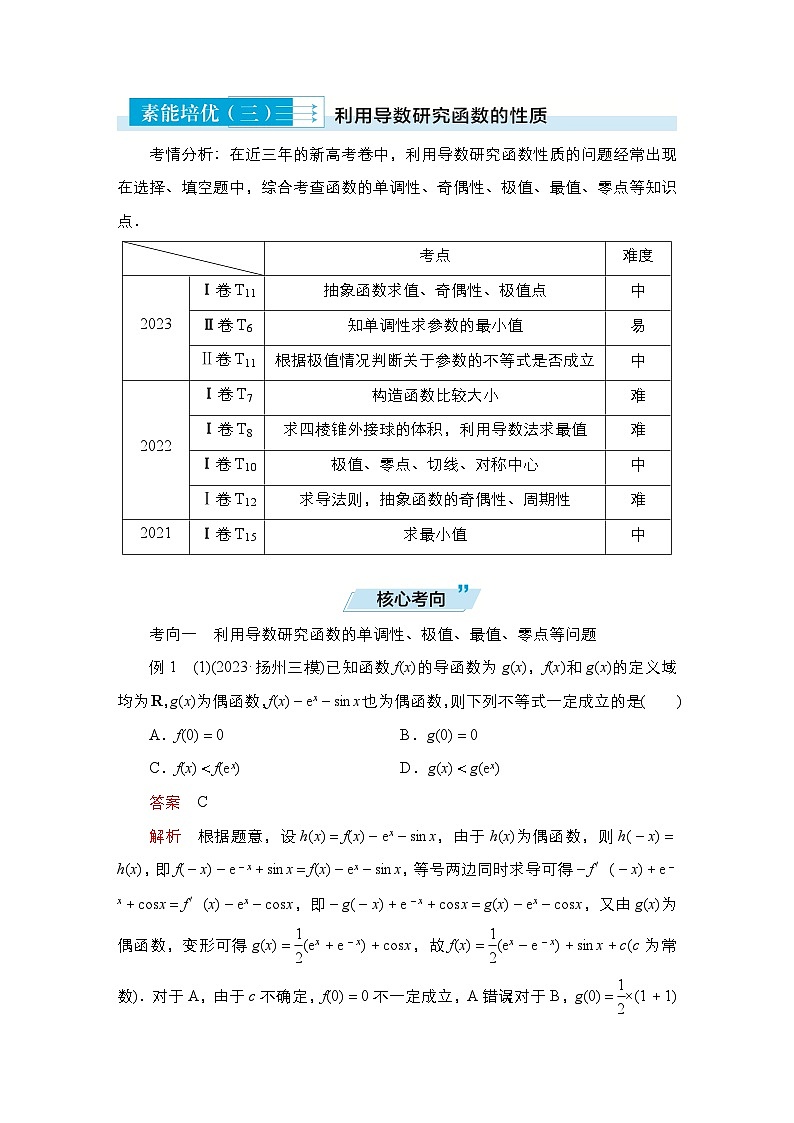
考向一 利用导数研究函数的单调性、极值、最值、零点等问题
例1 (1)(2023·扬州三模)已知函数f(x)的导函数为g(x)，f(x)和g(x)的定义域均为R，g(x)为偶函数，f(x)－ex－sinx也为偶函数，则下列不等式一定成立的是( )
A．f(0)＝0 B．g(0)＝0
C．f(x)＜f(ex) D．g(x)＜g(ex)
答案 C
解析 根据题意，设h(x)＝f(x)－ex－sinx，由于h(x)为偶函数，则h(－x)＝h(x)，即f(－x)－e－x＋sinx＝f(x)－ex－sinx，等号两边同时求导可得－f′(－x)＋e－x＋csx＝f′(x)－ex－csx，即－g(－x)＋e－x＋csx＝g(x)－ex－csx，又由g(x)为偶函数，变形可得g(x)＝eq \f(1,2)(ex＋e－x)＋csx，故f(x)＝eq \f(1,2)(ex－e－x)＋sinx＋c(c为常数)．对于A，由于c不确定，f(0)＝0不一定成立，A错误；对于B，g(0)＝eq \f(1,2)×(1＋1)＋1＝2，B错误；对于C，设F(x)＝ex－x，则F′(x)＝ex－1，当x∈(0，＋∞)时，F′(x)＝ex－1＞0，F(x)为增函数，当x∈(－∞，0)时，F′(x)＝ex－1＜0，F(x)为减函数，则F(x)≥F(0)＝1，故ex＞x在R上恒成立，又由g(x)＝eq \f(1,2)(ex＋e－x)＋csx≥1＋csx≥0，f(x)为R上的增函数，则f(x)＜f(ex)，C正确；对于D，g(x)为偶函数，其图象关于y轴对称，不能保证g(x)＜g(ex)成立，D错误．故选C.
(2)(多选)(2024·滁州模拟)对于函数f(x)＝eq \f(ln x,x2)，下列说法正确的是( )
A．f(x)在x＝eq \r(e)处取得极大值eq \f(1,2e)
B．若f(x)eq \f(e2,2)
C．f(eq \r(2))