

2021-2022学年辽宁省鞍山市千山区八年级上学期期中数学试题及答案
展开
这是一份2021-2022学年辽宁省鞍山市千山区八年级上学期期中数学试题及答案,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
下列各题的答案中只有一个是正确的,请把正确答案的序号填在题后的括号内.
1.如果一个多边形的内角和等于,则它的边数为()
A.6 B.5 C.4 D.3
2.下列四个图形中,线段是的高的是()
A.B.C.D.
3.如图,点B、F、C、E在一条直线上,,,那么添加下列一个条件后,仍无法判定的是()
A.B.C.D.
4.如图,,垂足分别为D、E,且,则直接判定与全等的理由是()
A.B.C.D.
5.一个多边形每一个外角都等于,则这个多边形的边数为().
A.10B.12C.16D.20
6.一个三角形的两边长分别为2和5,且第三边长为整数,这个三角形的周长最大值是()
A.11B.12C.13D.14
7.如图为6个边长相等的正方形的组合图形,则()
A.B.C.D.
8.中,、是角平分线,,则()
A. B. C. D.
9.如图,在等腰中,,D为的中点,过点D作,交于点F,交于点E.若,则的长为()
A.9B.8C.6D.4
10.如图,在中,,,是中线,过点B作于点F,过点C作交的延长线于点D.下列结论:①;②;③;④;⑤.正确的个数是()
A.5个B.4个C.3个D.2个
二、填空题(每小题2分,计16分)
11.点关于x轴的对称点的坐标为____________.
12.如图,在中,,平分,于D.如果,那么等于_____.
13.如图,在中,,,平分,,垂足为点D,那么______.
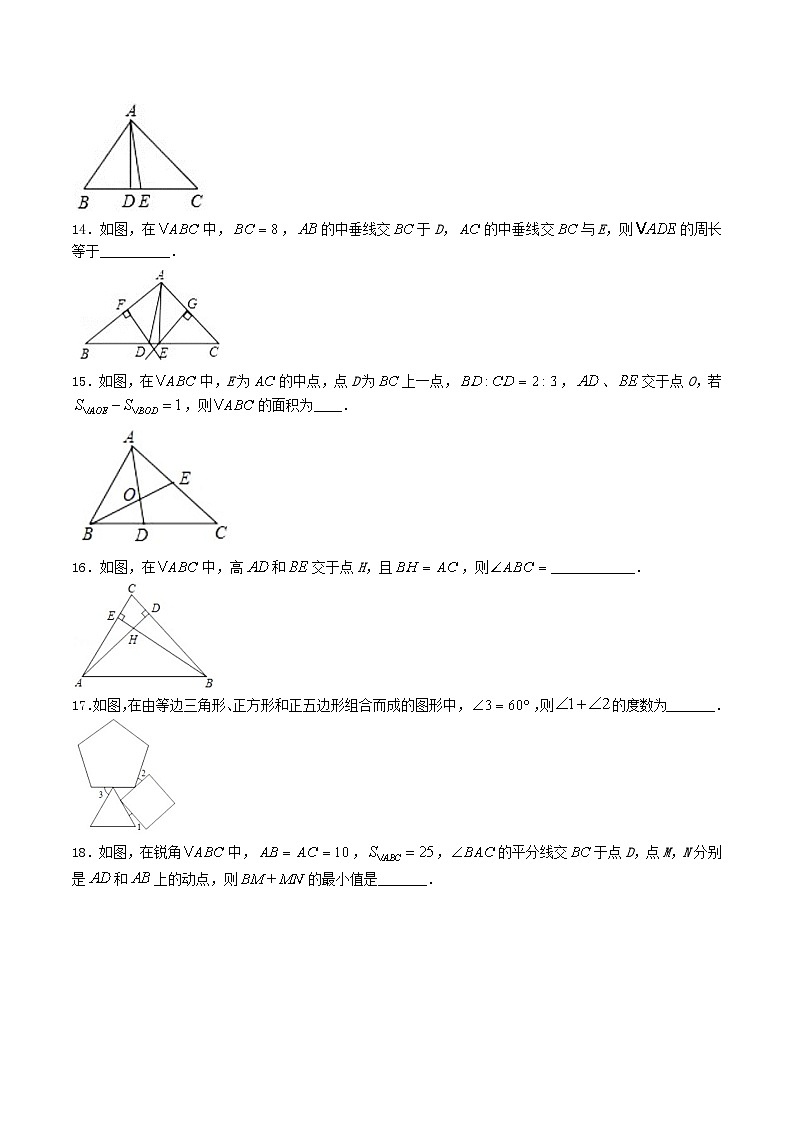
14.如图,在中,,的中垂线交于D,的中垂线交与E,则的周长等于__________.
15.如图,在中,E为的中点,点D为上一点,,、交于点O,若,则的面积为____.
16.如图,在中,高和交于点H,且,则____________.
17.如图,在由等边三角形、正方形和正五边形组合而成的图形中,,则的度数为_______.
18.如图,在锐角中,,,的平分线交于点D,点M,N分别是和上的动点,则的最小值是_______.
三、解答题(计64分)
19.(8分).如图,方格纸中每个小正方形的边长为1,四边形的顶点都在格点上.
(1)在方格纸上建立平面直角坐标系,使四边形的顶点A,C的坐标分别为,,并写出点D的坐标;
(2)在(1)中所建坐标系中,画出四边形关于x轴的对称图形,并写出点B的对应点的坐标.
20.(8分)如图,是的外角的平分线,且交的延长线于点E.
(1)若,,求的度数.
(2)求证:.
21.(8分)如图,中,,平分.若交于F,求证:.
22.(9分)如图,在四边形中,,E为的中点,连接并延长,交于点F.
(1)求证:;
(2)若,,求的长.
23.(9分)如图,在中,是角平分线,E,F分别为,上的点,且.
(1)求证:;
(2)与有何数量关系?请说明理由.
24.(10分)如图,是等边三角形,延长到E,使.点D是边的中点,连接并延长交于F求证:
(1);
(2).
25.(12分)如图,,,,,垂足为F.
(1)求证:;
(2)求的度数;
(3)求证:.
参考答案
一、选择题(每小题2分,计20分)
1.A2.C3.C 4.D 5.D 6.C7.B 8.A 9.B 10.B
二、填空题(每小题2分,计16分)
11.(﹣3,﹣2)12.10cm13.10°14.8 15.1016.45°
17.42°18.5
三、解答题(计64分)
19.(8分)解:(1)平面直角坐标系如图所示,D(﹣1,﹣2);……4分
(语言叙述1分,作图正确2分,坐标1分,)
(2)如图所示,四边形A1B1C1D1即为所求,B1(﹣4,5).……8分
(语言叙述1分,作图正确2分,坐标1分)
20.(8分)(1)∵CE是△ABC的外角∠ACD的平分线,
∴∠DCE=∠DCA=(180°-∠ACB)=70°,……2分
∴∠E=∠DCE-∠ABC=40°;……3分
(2)证:∵CE是△ABC的外角∠ACD的平分线,
∴∠ACE=∠DCE,……4分
∵∠DCE=∠B+∠E,……5分
∴∠ACE=∠B+∠E,……6分
∴∠BAC=∠ACE+∠E=∠B+∠E+∠E=∠B+2∠E.……8分
21.(8分)证明:∵∠BAC=180°-∠B-∠C,∠B=2∠C……1分
∴∠BAC=180°-3∠C……2分
∵AE平分∠BAC
∴……3分
∵AE⊥EF∴∠AEF=90°……4分
∴……6分
∴……7分
∴∠C=2∠FEC.……8分
22.(9分)证明:(1)证明:∵AD∥BC,
∴∠DAE=∠FCE,∠ADE=∠EFC.……1分
又∵E为AC的中点,
∴AE=CE.……2分
在△ADE和△CFE中,
,……4分
∴△ADE≌△CFE(AAS).……5分
∴DE=EF.……6分
(2)解:∵△ADE≌△CFE,
∴AD=CF=12,……7分
∵BF:CF=2:3,
∴BF=8,……8分
∴BC=BF+CF=8+12=20.……9分
23.(9分(1)证明:(1),……1分
……3分
(2),……4分
理由如下:
过点D分别作于点M,于点N,……5分
,……6分
是角平分线,
,……7分
,……8分
……9分
24.(10分)证明:(1)∵△ABC是等边三角形,
∴AC=BC,∠ACB=∠B=60°,……1分
∵D为AC的中点,
∴AD=CDAC,……2分
∵CEBC,∴CD=CE,……3分
∵∠E+∠CDE=∠ACB=60°,
∴∠E=∠CDE=30°,
∵∠B=60°,
∴∠EFB=180°﹣60°﹣30°=90°,……4分
即EF⊥AB;……5分
(2)连接BD,……6分
∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,……7分
∵D为AC的中点,
∴∠DBC=∠ABDABC=30°,……8分
∵∠E=30°,∴∠DBC=∠E,……9分
∴DE=BD,
∵∠BFE=90°,∠ABD=30°,∴BD=2DF,
即DE=2DF.……10分
25.(12分)证明:(1)∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,
∴∠BAC=∠DAE,
在△ABC和△ADE中,
,……2分
∴△BAC≌△DAE(SAS);……3分
(2)∵∠CAE=90°,AC=AE,
∴∠E=45°,……4分
由(1)知△ABC≌△ADE,
∴∠BCA=∠E=45°,……4分
∵AF⊥BC,∴∠CFA=90°,
∴∠CAF=45°,……5分
∴∠FAE=∠FAC+∠CAE=45°+90°=135°;……6分
(3)延长BF到G,使得FG=FB,……7分
∵AF⊥BG,
∴∠AFG=∠AFB=90°,
在△AFB和△AFG中,
,……8分
∴△AFB≌△AFG(SAS),
∴AB=AG,∠ABF=∠G,
∵△BAC≌△DAE,
∴AB=AD,∠CBA=∠EDA,CB=ED,
∴AG=AD,∠ABF=∠CDA,
∴∠G=∠CDA,……9分
在△CGA和△CDA中,
,……10分
∴△CGA≌△CDA,
∴CG=CD,……11分
∵CG=CB+BF+FG=CB+2BF=DE+2BF,
∴CD=2BF+DE.……12分
相关试卷
这是一份331,辽宁省鞍山市千山区2023-2024学年八年级上学期12月月考数学试题,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份辽宁省鞍山市千山区2023-2024学年七年级上学期期中考试数学试题,共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份辽宁省鞍山市千山区2022-2023学年九年级上学期期末数学试题(含答案),共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。








