辽宁省盘锦市兴隆台区盘锦市第一完全中学2023-2024学年七年级下学期开学数学试题（解析版）

这是一份辽宁省盘锦市兴隆台区盘锦市第一完全中学2023-2024学年七年级下学期开学数学试题（解析版），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

注意：所有试题必须在答题卡上作答，在本试卷上作答无效．
一、选择题（请将正确答案的序号涂在答题卡上．每小题3分，共30分）
1. 如图，下列条件中不能判定的是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】根据平行线的判定逐项判断即可．
【详解】解：A、∵，
∴，不能判定，则此项符合题意；
B、∵，
∴（内错角相等，两直线平行），则此项不符合题意；
C、∵，
∴（同旁内角互补，两直线平行），则此项不符合题意；
D、∵，
∴（同位角相等，两直线平行），则此项不符合题意；
故选：A．
【点睛】本题考查了平行线的判定，能灵活运用平行线的判定进行推理是解题关键．
2. 如图，把一块含有的直角三角形的两个顶点放在直尺的对边上，若，则的度数是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题主要考查了平行线的性质，三角板中角度的计算．先由平行线的性质得到，再根据，即可得到．
【详解】解：如图所示，∵，
∴，
∵三角板为含有角的直角三角板，
∴，
∴，
故选：C．
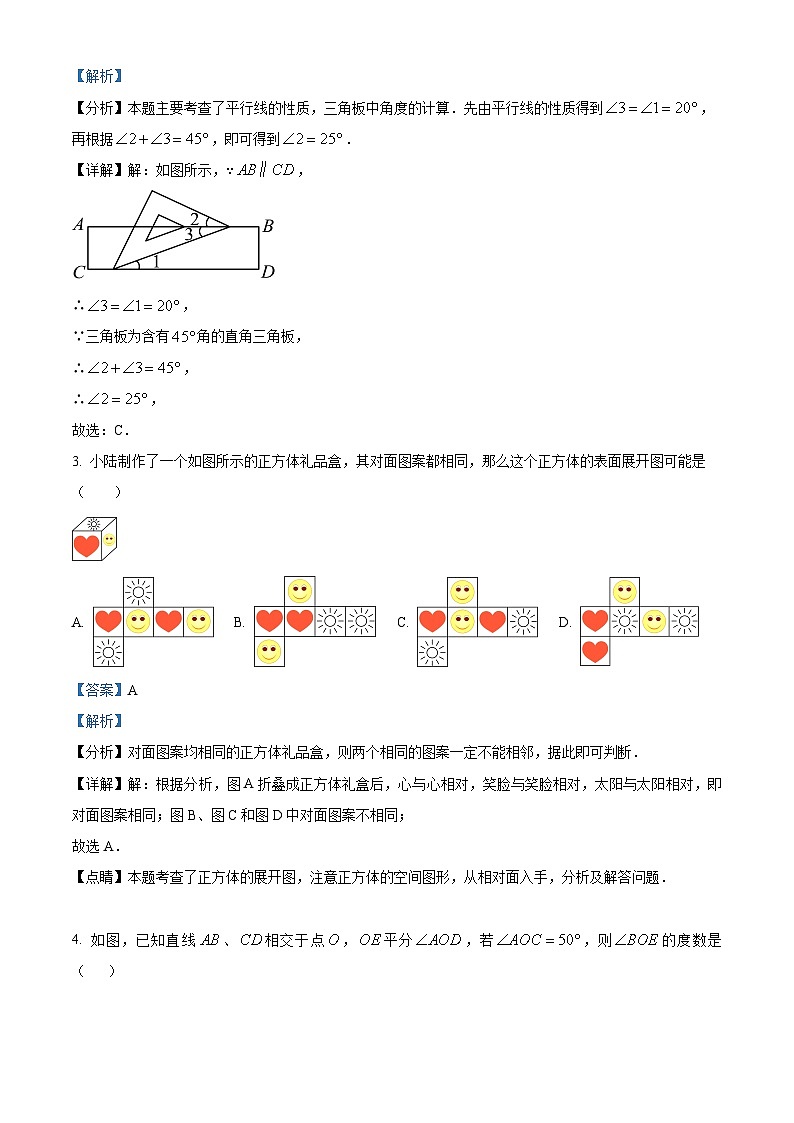
3. 小陆制作了一个如图所示的正方体礼品盒，其对面图案都相同，那么这个正方体的表面展开图可能是（ ）

A. B. C. D.
【答案】A
【解析】
【分析】对面图案均相同的正方体礼品盒，则两个相同的图案一定不能相邻，据此即可判断．
【详解】解：根据分析，图A折叠成正方体礼盒后，心与心相对，笑脸与笑脸相对，太阳与太阳相对，即对面图案相同；图B、图C和图D中对面图案不相同；
故选A．
【点睛】本题考查了正方体的展开图，注意正方体的空间图形，从相对面入手，分析及解答问题．
4. 如图，已知直线、相交于点，平分，若，则的度数是（ ）

A. B. C. D.
【答案】D
【解析】
【分析】首先根据邻补角求得，再根据角平分线的定义可得，进而得到的度数，然后根据邻补角求得的度数．
【详解】解：∵，，
∴，
平分，
，
，
．
故选：D．
【点睛】此题主要考查了邻补角的性质，角平分线的定义，关键是掌握邻补角性质．
5. 如图1，A、B两个村庄在一条河l（不计河的宽度）的两侧，现要建一座码头，使它到A、B两个村庄的距离之和最小．如图2，连接AB，与l交于点C，则C点即为所求的码头的位置，这样做的理由是（ ）
A. 垂线段最短B. 两点确定一条直线
C. 两点之间，线段最短D. 平行于同一条直线的两条直线平行
【答案】C
【解析】
【分析】利用线段的性质解答即可．
【详解】解：A，B两个村庄在一条河l（不计河的宽度）的两侧，现要建一座码头，使它到A、B两个村庄的距离之和最小，图2中所示的C点即为所求的码头的位置，那么这样做的理由是两点之间，线段最短.
故选：C．
【点睛】此题主要考查了线段的性质，关键是掌握两点之间，线段最短．
6. 如图，给出下列判断：①与是同位角；②与是同旁内角；③与是内错角；④与是同位角．其中正确的是（ ）
A. ①②B. ①②④C. ②③④D. ①③④
【答案】A
【解析】
【分析】根据同位角、同旁内角、内错角的定义进行判断即可．
【详解】解：由题意知，与是同位角，①正确，故符合要求；
与是同旁内角，②正确，故符合要求；
与不是内错角，③错误，故不符合要求；
与是内错角，④错误，故不符合要求；
∴正确的是①②，
故选：A．
【点睛】本题考查了同位角、同旁内角、内错角的定义．解题的关键在于对知识的熟练掌握．
7. 下列命题中，真命题的个数是（ ）
①对顶角相等；
②两直线平行，同旁内角相等；
③平行于同一条直线的两直线平行；
④若正数a，b满足，则
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
【分析】本题主要考查命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．根据对顶角相等，平行线的判定与性质及开方运算，对各小题分析判断即可得解．
【详解】解：①根据对顶角的性质，对顶角相等，所以①是真命题．
②两直线平行，同旁内角互补，所以②是假命题．
③平行于同一条直线的两直线平行，所以③是真命题．
④因为a，b是正数，且满足，两边开方，得到所以④是真命题．综上所述，真命题有①③④共3个．
故选C．
8. 如图所示的四种沿AB进行折叠的方法中，不一定能判断纸带两条边a，b互相平行的是（ ）
A. 如图1，展开后测得∠1=∠2B. 如图2，展开后测得∠1=∠2且∠3=∠4
C. 如图3，测得∠1=∠2D. 在图4中，展开后测得∠1+∠2=180°
【答案】C
【解析】
【分析】根据平行线的判定定理，进行分析，即可解答．
【详解】A、 当∠1=∠2时，内错角相等，两直线平行，所以；
B、由∠1=∠2且∠3=∠4可得∠1=∠2=∠3=∠4=90∘，所以；
C、∠1=∠2不能判定a，b互相平行；
D、∠1+∠2=180°时，同旁内角互补，两直线平行，所以．
故选：C．
【点睛】本题考查平行线判定，掌握平行线的判定定理是解题的关键．同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．
9. 如图，直线 ，，，则（ ）
A. 30°B. 35 °C. 36°D. 40°
【答案】D
【解析】
【分析】根据三角形的外角定理可得，，再根据平行线的性质可得，即可求解．
【详解】解：根据题意可得：
，，
∴，
∵，
∴，
∴，
故选：D．
【点睛】本题主要考查了三角形的外角定理以及平行线的性质，解题的关键是掌握“三角形的一个外角定于与它不相邻的两个内角之和”，“两直线平行，同旁内角互补”．
10. 如图，，F为上一点，，且平分，过点F作于点G，且，则下列结论：①；②；③平分；④平分．其中正确结论的个数是（ ）
A. 1个B. 2个C. 3个D. 4个
【答案】A
【解析】
【分析】此题考查了角平分线的定义和平行线的性质，解题的关键是熟练掌握平行线的性质；延长，交于I，根据角平分线的定义和平行线的性质即可解答；
【详解】解：延长，交于I．
，
，
，
，
平分，
，
，
，
，
，
∴①错误；②正确，
∵平分，
，
，
，
可见，的值未必为，未必为，只要和为即可，
∴③，④不一定正确．
故选：．
二、填空题
11. 如图是一种对顶角量角器，它所测量的角的度数是______，用它测量角的原理是______．

【答案】 ①. ②. 对顶角相等
【解析】
【分析】根据量角器的使用方法，对顶角的性质即可求解．
【详解】解：如图所示，

量角器上，
∵与是对顶角，
∴，
故答案为：，对顶角相等．
【点睛】本题主要考查对顶角相等，理解图示，掌握对顶角的性质是解题的关键．
12. 若，则的补角的度数为______.
【答案】
【解析】
【分析】本题主要考查了求一个角的补角，解题的关键是熟练掌握互为补角的两个角和为．
【详解】解：，
即的补角的度数为．
故答案为：．
13. 如图，直线 AB ，CD 相交于点O ，若∠EOC ：∠EOD=4 ：5 ，OA平分∠EOC ，则∠BOE=___________．

【答案】140°
【解析】
【分析】直接利用平角的定义得出：∠COE=80°，∠EOD=100°，进而结合角平分线的定义得出∠AOC=∠BOD，进而得出答案．
【详解】∵∠EOC：∠EOD=4：5，
∴设∠EOC=4x，∠EOD=5x，
故4x+5x=180°，
解得：x=20°，
可得：∠COE=80°，∠EOD=100°，
∵OA平分∠EOC，
∴∠COA=∠AOE=40°，
∴∠BOE=180°-∠AOE=140°．
故答案140°.
【点睛】此题主要考查了角平分线的定义以及邻补角，正确把握相关定义是解题关键.
14. 如图，直线m//n，以直线m上的点A为圆心，适当长为半径画弧，分别交直线m，n于点C，B，连接AB，BC．若∠1=40°，则∠ABC的度数为__________．
【答案】70°
【解析】
【分析】由直线，可得到∠BAC=∠1=30°，然后根据等腰三角形以及三角形内角和定理，可求出∠ABC的度数．
【详解】解：∵直线m∥n，
∴∠BAC=∠1=40°，
由题意可知AB=BC，
∴∠ABC=∠ACB，
∴∠ABC=（180°-∠BAC）=（180°-40°）=70°，
故答案为70°．
【点睛】本题主要考查了平行线的性质以及三角形的内角和定理，熟练掌握两直线平行，内错角相等是解题的关键．
15. 已知线段，是直线上的一点，且，那么、两点的距离是____．
【答案】8或16
【解析】
【分析】先根据线段的关系求出，再分点在线段上，点在线段的延长线上，两种情况利用线段的和差关系求解即可．
【详解】解：，，
，
①如图1，点在线段上，则；
②如图2，点在线段的延长线上，．
综上所述，两点的距离是8或16．
故答案为：8或16．
【点睛】本题主要考查了线段的和差计算，正确画出对应的图形利用分类讨论的思想求解是解题的关键．
16. 如图，中，，点为边上一点，将沿直线折叠后，点落到点处，若，则的度数为___．
【答案】110
【解析】
【分析】本题考查了折叠的性质，平行线的性质根据平行线的性质得到，根据折叠的性质得到，根据平角的定义可得，由此可以求出的度数即可得到答案．
【详解】解：，，
，
由折叠的性质得，
，，
，
，
．
故答案为：110．
17. 如图是一种躺椅及其简化结构示意图，扶手AB与底座都平行于地面，靠背与支架平行，前支架与后支架分别与交于点G和点D，与交于点N，当前支架与后支架正好垂直，时，人躺着最舒服，则此时扶手与靠背的夹角___________．

【答案】##122度
【解析】
【分析】由可求得的度数，再根据即可求出的度数．
【详解】解：∵，，
∴．
∵，
∴，
∴．
∵，
故答案为：．
【点睛】本题考查了平行线的性质，垂直的定义，熟练掌握平行线的性质是解答本题的关键．
18. 将一副直角三角板按如图1所示位置摆放，其中，，．若将三角板绕点A按每秒的速度顺时针旋转，如图2，在此过程中，设旋转时间为t秒，当线段与三角板的一条边平行时，________________．

【答案】秒或秒或秒
【解析】
【分析】由线段与三角板的一条边平行可知有三种情况：（1）当时，点E落在线段上，由此可求出旋转角，进而可求出t的值；（2）当时，则，由此可求出旋转角，进而可求出t的值；（3）当，则，由此可求出旋转角，进而可求出t的值．
【详解】解：设旋转角为α，则旋转的时间（秒），
在顺时针旋转的过程中，线段与三角板的一条边平行，
有以下三种情况：
（1）当时，
，
∴点E落在线段上时，

旋转角，
（秒）；
（2）当时，则，

，
，
旋转角，
（秒）；
（3）当时，则，

，
旋转角，
（秒）；
综上所述：秒或秒或秒．
故答案为：秒或秒或秒．
【点睛】此题主要考查了图形的旋转变换与性质，平行线的判定，解答此题的关键是熟练掌握平行线的判定和性质，难点是利用分类讨论的思想进行分类讨论．
三、解答题（共46分）
19. 如图，直线AB、CD相交于，，．
（1）求的度数；
（2）试说明平分．
【答案】（1）
（2）见解析
【解析】
【分析】本题考查了邻补角的定义，补角的定义，角平分线的定义，掌握角平分线的定义及邻补角的定义是解题的关键．
（）先根据已知条件和邻补角的性质求出的度数，然后即可求出的度数；
（）根据补角的定义可知即可解答．
【小问1详解】
解：∵直线AB、CD相交于，，
∴，
∵，
∴，
即的度数为；
【小问2详解】
解：∵直线AB、CD相交于，，
∴，
∵，
∴，
∵，
∴，
∴，
故平分．
20. 已知：如图，．
（1）判断与的位置关系，并说明理由．
（2）若平分，若，求的度数．
【答案】（1）．理由见解析
（2）
【解析】
【分析】本题考查了平行线的判定和性质，角平分线的性质；
（1）根据可得，从而证明，根据平行线的判定即可证明结论；
（2）根据平行线的性质和角平分线的性质求解即可．
【小问1详解】
解：．
理由：∵，
∴，
又∵，
∴，
∴；
【小问2详解】
∵，
∴，
∵平分，
∴，
∵，
∴．
21 请解答下列各题：
（1）阅读并回答：科学实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等．如图1，一束平行光线与射向一个水平镜面后被反射，此时，．
①由条件可知：，依据是 ，，依据是 ．
②反射光线与平行，依据是 ．
（2）解决问题：如图2，一束光线射到平面镜上，被反射到平面镜上，又被镜反射，若射出的光线平行于，且，则 ； ．
【答案】（1）①两直线平行，同位角相等；等量代换．②同位角相等，两直线平行．（2）84°；90°；
【解析】
【分析】（1）根据平行线的判定与性质逐一求解可得；
（2）根据入射角等于反射角得出∠1=∠4，∠5=∠7，求出∠6，根据平行线性质即可求出∠2，求出∠5，根据三角形内角和求出∠3即可．
【详解】解：（1）①由条件可知：∠1=∠3，依据是：两直线平行，同位角相等；
∠2=∠4，依据是：等量代换；
②反射光线BC与EF平行，依据是：同位角相等，两直线平行；
故答案：①两直线平行，同位角相等；等量代换．②同位角相等，两直线平行．
（2）如图，
∵∠1=42°，
∴∠4=∠1=42°，
∴∠6=180°42°42°=96°，
∵m∥n，
∴∠2+∠6=180°，
∴∠2=84°，
∴∠5=∠7=，
∴∠3=180°48°42°=90°．
故答案为：84°；90°；
【点睛】本题考查了平行线的性质和判定，三角形的内角和定理的应用，熟练掌握平行线的判定与性质是解题的关键．
22. 如图，在中，D、E、F三点分别在上，过点D的直线与线段相交于点M，已知

（1）说明：
（2）若，，，求的度数．
【答案】（1）见解析 （2）
【解析】
【分析】（1）根据邻补角及题意得出，再由平行线的判定证明即可；
（2）根据平行线的判定和性质得出，再由三角形内角和定理求解即可．
【小问1详解】
证明：∵，
∴
∴；
【小问2详解】
∵，
∴，
∵
∴ ，
又∵，
∴．
∵，
∴，
∴．
∴．
【点睛】题目主要考查平行线的判定和性质及三角形内角和定理，找准各角之间的关系是解题关键．
23. 探索发现：如图是一种网红弹弓的实物图，在两头上系上皮筋，拉动皮筋可形成平面示意图如图1图2，弹弓的两边可看成是平行的，即．各活动小组探索与，之间的数量关系．已知，点P不在直线和直线上，在图1中，智慧小组发现：．智慧小组是这样思考的：过点P作，……．

（1）填空：过点P作．
∴，
∵，，
∴ ( )，
∴，
∴，
即．
（2）在图2中，猜测与之间的数量关系，并完成证明．
（3）善思小组提出：
①如图3，已知，则角之间的数量关系为 ．(直接填空)
②如图4，，，分别平分，．则与之间的数量关系为 ．(直接填空)
【答案】（1）平行于同一直线的两直线平行
（2）；证明见解析
（3）①；②
【解析】
【分析】（1）发现由平行线的性质得出，由，，推出，得出，推出，即可得出结论；
（2）过点P作，由平行线的性质得出，由，，推出，得出，则；
（3）①过点M作，由平行线的性质得出，由，推出，得出，即可得出结果；
②过点P作，过点F作，由平行线的性质得出，，由角平分线的性质得出，即，由，，推出，得出，，由角平分线的性质得出，即，推出，，即可得出结果．
【小问1详解】
解：填空：过点P作．
∴，
∵，，
∴ (平行于同一直线的两直线平行)，
∴，
∴，
即．
故答案为：平行于同一直线的两直线平行；
【小问2详解】
；
证明：过点P作，如图2所示：

∴，
∵，，
∴，
∴，
∴；
【小问3详解】
)①；理由如下：
过点M作，如图3所示：

∴，
∵，
∴，
∴，
∵，
∴，
∴，
故答案为：；
②；
证明：过点P作，过点F作，如图4所示：

∴，
∵平分，
∴，
∴，
∵，，
∴，
∴，，
∵平分，
∴，
∴，
∴，
，
∴．
故答案为：．
【点睛】本题考查平行线判定与性质，角平分线有关的计算，掌握平行线的判定与性质是解题的关键．注意此类问题(拐点问题)过拐点作平行线是解决此类问题的技巧．