四川省百师联盟2024届高三冲刺卷（二）全国卷文科数学试题（原卷版）

这是一份四川省百师联盟2024届高三冲刺卷（二）全国卷文科数学试题（原卷版），共6页。试卷主要包含了 已知函数为奇函数，则， 世界三大数学猜想分别为等内容，欢迎下载使用。
注意事项：
1.答卷前，考生务必将自己的姓名、考场号、座位号、准考证号填写在答题卡上.
2.回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.
3.考试结束后，将本试卷和答题卡一并交回.
考试时间为120分钟，满分150分
一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1. 已知集合，. 则（ ）
A. B. C. D.
2. 过点，且焦点在轴上的抛物线的标准方程是（ ）
A. B. C. D.
3. 在中，则（ ）
A. B.
C. D.
4. 已知函数为奇函数，则（ ）
A. B. 0C. 1D.
5. 已知，是两条不同的直线，，，是三个不同的平面，下列命题为真命题的是（ ）
A. 若，，则B. 若，，，则
C. 若，，则D. ，，，则
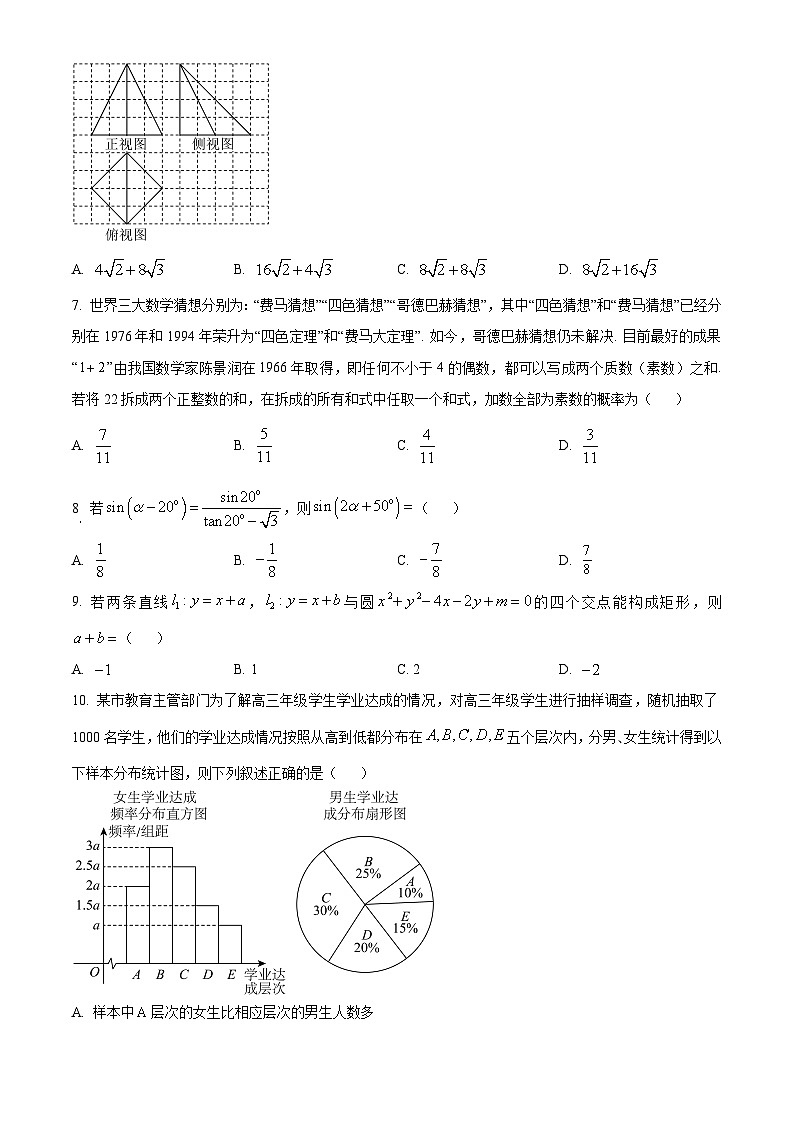
6. 某几何体三视图如图所示，其中每个网格是由边长为1的小正方形组成，则该几何体的侧面积为（ ）

A. B. C. D.
7. 世界三大数学猜想分别为：“费马猜想”“四色猜想”“哥德巴赫猜想”，其中“四色猜想”和“费马猜想”已经分别在1976年和1994年荣升为“四色定理”和“费马大定理”. 如今，哥德巴赫猜想仍未解决. 目前最好的成果“”由我国数学家陈景润在1966年取得，即任何不小于4的偶数，都可以写成两个质数（素数）之和. 若将22拆成两个正整数的和，在拆成的所有和式中任取一个和式，加数全部为素数的概率为（ ）
A. B. C. D.
8 若，则（ ）
A. B. C. D.
9. 若两条直线，与圆的四个交点能构成矩形，则（ ）
A. B. 1C. 2D.
10. 某市教育主管部门为了解高三年级学生学业达成的情况，对高三年级学生进行抽样调查，随机抽取了1000名学生，他们的学业达成情况按照从高到低都分布在五个层次内，分男､女生统计得到以下样本分布统计图，则下列叙述正确的是（ ）
A. 样本中层次的女生比相应层次的男生人数多
B. 估计样本中男生学业达成的中位数比女生学业达成的中位数小
C. 层次的女生和层次的男生在整个样本中频率相等
D. 样本中层次学生数和层次的学生数一样多
11. 在中，三个内角，，所对的边分别为，，，且，若，，则（ ）
A. 1B. 2C. D. 4
12. 2023年6月22日，由中国帮助印尼修建的雅万高铁测试成功，高铁实现时速自动驾驶，不仅速度比普通列车快，而且车内噪声更小．如果用声强（单位：）表示声音在传播途径中每平方米上的声能流密度，声强级（单位：）与声强的函数关系式为，其中为基准声强级，为常数，当声强时，声强级．下表为不同列车声源在距离处的声强级：
设在离内燃列车､电力列车､高速列车处测得的实际声强分别为，则下列结论正确的是（ ）
A. B. C. D.
二、填空题：本题共4小题，每小题5分，共20分.
13. 已知复数（为虚数单位），则的虚部为______.
14. 已知函数的图象在点处的切线方程是，若，则的值为______.
15. 已知函数的最小正周期为，则下列结论中正确的有______.
①函数的图象关于直线对称；
②函数的对称中心是；
③函数区间上单调递增；
④函数的图象可以由的图象向右平移个单位长度得到.
16. 已知双曲线C:x2a2-y2b2=1a>0,b>0左、右焦点分别为，. 点A在双曲线上，点在轴上，，，则双曲线的渐近线方程为______.
三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.
（一）必考题：60分.
17. 已知正项数列满足，等差数列的前项和为，且．
（1）求数列的通项公式；
（2）若，求数列的前项和．
18. 芯片作为集成电路的载体，广泛应用在手机、军工、航天等多个领域，是能够影响一个国家现代工业的重要因素. 根据市场调研与统计，某公司自2018年起的五年时间里在芯片技术上的研发投入（单位：亿元）与收益（单位：亿元）的数据统计如下：
（1）根据表格中的数据，在给出的坐标系中画出散点图，并判断与是否线性相关；
（2）若与线性相关，求出关于的回归方程，并预测2023年底该公司的收益.
参考公式：回归方程中斜率和截距的最小二乘法估计公式分别为，；
参考数据：，，，，.
19. 如图，在直角梯形中，，，，，，分别是，上的点，且，现将四边形沿向上折起成直二面角，设.
（1）若，在边上是否存在点，满足，使得平面？若存在，求出；若不存在，说明理由.
（2）当三棱锥的体积最大时，求点到平面的距离.
20. 已知椭圆的左、右焦点分别为，，左顶点为，离心率为，短轴长为.
（1）求椭圆的标准方程；
（2）不垂直于坐标轴的直线交椭圆于，两点，，与不重合，直线与的斜率之积为. 证明：直线过定点.
21. 已知函数，.
（1）求的极值；
（2）证明：.
（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题.
[选修4-4：坐标系与参数方程]
22. 在平面直角坐标系中，直线的方程为：，以坐标原点为极点，轴的非负半轴为极轴建立极坐标系，曲线的极坐标方程为．
（1）①若直线上的动点与定点满足，求以为参数的直线的参数方程；
②求曲线的直角坐标方程；
（2）设直线与曲线的交点为，求弦长的值．
[选修4-5：不等式选讲]
23. 已知函数．
（1）当时，求不等式的解集；
（2）当时，若恒成立，求实数的取值范围．
声源
与声源的距离（单位：）
声强级范围
内燃列车
20
电力列车
20
高速列车
20
年份
2018
2019
2020
2021
2022
投入
1
2
3
4
5
收益
23.1
37.0
62.1
111.6
150.8