专题19 解三角形大题综合（学生卷）- 十年（2015-2024）高考真题数学分项汇编（全国通用）

这是一份专题19 解三角形大题综合（学生卷）- 十年（2015-2024）高考真题数学分项汇编（全国通用），共10页。试卷主要包含了记的内角的对边分别为，已知，在中，已知，，.，的内角的对边分别为，已知，的内角的对边分别为已知.，已知分别是内角的对边， ，设.等内容，欢迎下载使用。


考点01 求面积的值及范围或最值
1．（2024·北京·高考真题）在中，内角的对边分别为，为钝角，，．
(1)求；
(2)从条件①、条件②、条件③这三个条件中选择一个作为已知，使得存在，求的面积．
条件①：；条件②：；条件③：．
注：如果选择的条件不符合要求，第（2）问得0分；如果选择多个符合要求的条件分别解答，按第一个解答计分．
2．（2023·全国甲卷·高考真题）记的内角的对边分别为，已知．
(1)求；
(2)若，求面积．
3．（2023·全国乙卷·高考真题）在中，已知，，.
(1)求；
(2)若D为BC上一点，且，求的面积.
4．（2022·浙江·高考真题）在中，角A，B，C所对的边分别为a，b，c．已知．
(1)求的值；
(2)若，求的面积．
5．（2019·全国·高考真题）的内角的对边分别为，已知．
（1）求；
（2）若为锐角三角形，且，求面积的取值范围．
6．（2017·全国·高考真题）的内角的对边分别为已知.
（1）求角和边长；
（2）设为边上一点，且,求的面积.
7．（2016·全国·高考真题）的内角A，B，C的对边分别为a，b，c.已知.
（1）求角C；（2）若，，求的周长.
8．（2015·浙江·高考真题）在中，内角A，B，C所对的边分别为.已知.
（1）求的值；
（2）若，求的面积.
9．（2015·全国·高考真题）已知分别是内角的对边， ．
（1）若，求
（2）若，且求的面积．
10．（2015·山东·高考真题）设.
（Ⅰ）求的单调区间；
（Ⅱ）在锐角中，角的对边分别为,若,求面积的最大值.
考点02 求边长、周长的值及范围或最值
1．（2024·全国新Ⅱ卷·高考真题）记的内角A，B，C的对边分别为a，b，c，已知．
(1)求A．
(2)若，，求的周长．
2．（2024·全国新Ⅰ卷·高考真题）记的内角A、B、C的对边分别为a，b，c，已知，
(1)求B；
(2)若的面积为，求c．
3．（2023·全国新Ⅱ卷·高考真题）记的内角的对边分别为，已知的面积为，为中点，且．
(1)若，求；
(2)若，求．
4．（2022·全国新Ⅱ卷·高考真题）记的内角A，B，C的对边分别为a，b，c，分别以a，b，c为边长的三个正三角形的面积依次为，已知．
(1)求的面积；
(2)若，求b．
5．（2022·全国乙卷·高考真题）记的内角的对边分别为，已知．
(1)证明：；
(2)若，求的周长．
6．（2022·北京·高考真题）在中，．
(1)求；
(2)若，且的面积为，求的周长．
7．（2022·全国新Ⅰ卷·高考真题）记的内角A，B，C的对边分别为a，b，c，已知．
(1)若，求B；
(2)求的最小值．
8．（2020·全国·高考真题）的内角A，B，C的对边分别为a，b，c.已知B=150°.
（1）若a=c，b=2，求的面积；
（2）若sinA+sinC=，求C.
9．（2020·全国·高考真题）中，sin2A－sin2B－sin2C=sinBsinC．
（1）求A；
（2）若BC=3，求周长的最大值.
10．（2018·全国·高考真题）在平面四边形中，，，，.
（1）求；
（2）若，求.
11．（2017·全国·高考真题）△ABC的内角的对边分别为,已知△ABC的面积为
(1)求;
(2)若求△ABC的周长.
12．（2017·山东·高考真题）在△ABC中,角A,B,C的对边分别为a,b,c,已知b=3,,S△ABC=3,求A和a.
13．（2017·全国·高考真题）△ABC的内角的对边分别为，已知．
（1）求；
（2）若，△ABC的面积为2，求．
14．（2016·全国·高考真题）的内角A，B，C的对边分别为a，b，c.已知.
（1）求角C；（2）若，，求的周长.
15．（2015·浙江·高考真题）在中，内角 ，， 所对的边分别为， ，，已知 ，= .
（1）求的值；
（2）若的面积为3，求 的值.
16．（2015·山东·高考真题）中，角所对的边分别为.已知 求 和 的值.
考点03 求角和三角函数的值及范围或最值
1．（2024·天津·高考真题）在中，角所对的边分别为，已知．
(1)求；
(2)求；
(3)求的值．
2．（2023·天津·高考真题）在中，角所对的边分别是．已知．
(1)求的值；
(2)求的值；
(3)求的值．
3．（2022·天津·高考真题）在中，角A、B、C的对边分别为a，b，c.已知.
(1)求的值；
(2)求的值；
(3)求的值.
4．（2021·天津·高考真题）在，角所对的边分别为，已知，．
（I）求a的值；
（II）求的值；
（III）求的值．
5．（2021·全国新Ⅰ卷·高考真题）记是内角，，的对边分别为，，.已知，点在边上，.
（1）证明：；
（2）若，求.
6．（2020·天津·高考真题）在中，角所对的边分别为．已知 ．
（Ⅰ）求角的大小；
（Ⅱ）求的值；
（Ⅲ）求的值．
7．（2020·浙江·高考真题）在锐角△ABC中，角A，B，C的对边分别为a，b，c，且．
（I）求角B的大小；
（II）求csA+csB+csC的取值范围．
8．（2020·江苏·高考真题）在△ABC中，角A，B，C的对边分别为a，b，c，已知．
（1）求的值；
（2）在边BC上取一点D，使得，求的值．
9．（2019·江苏·高考真题）在△ABC中，角A，B，C的对边分别为a，b，c．
（1）若a=3c，b=，csB=，求c的值；
（2）若，求的值．
10．（2019·北京·高考真题）在△ABC中，a=3，b−c=2，csB=．
（Ⅰ）求b，c的值；
（Ⅱ）求sin（B–C）的值．
11．（2019·全国·高考真题）的内角A，B，C的对边分别为a，b，c，设．
（1）求A；
（2）若，求sinC．
12．（2018·天津·高考真题）在中，内角A，B，C所对的边分别为a，b，c.已知.
（1）求角B的大小；
（2）设a=2，c=3，求b和的值.
13．（2017·天津·高考真题）在中，内角所对的边分别为.已知，.
（I）求的值；
（II）求的值.
14．（2017·天津·高考真题）在中，内角所对的边分别为.已知，，.
（Ⅰ）求和的值；
（Ⅱ）求的值.
15．（2016·四川·高考真题）在ABC中，角A，B，C所对的边分别是a，b，c，且.
（Ⅰ）证明：sinAsinB=sinC；
（Ⅱ）若，求tanB．
16．（2016·浙江·高考真题）在ABC中，内角所对的边分别为a，b，c.已知b+c=2acs B.
（Ⅰ）证明：A=2B；
（Ⅱ）若cs B=，求cs C的值．
17．（2016·浙江·高考真题）在中，内角所对的边分别为，已知．
（1）证明：；
（2）若的面积，求角的大小．
18．（2016·天津·高考真题）在中，内角所对的边分别为a,b,c，已知.
（Ⅰ）求B；
（Ⅱ）若，求sinC的值.
19．（2016·北京·高考真题）在△ABC中，(1)求B的大小；
(2)求cs A＋cs C的最大值．
20．（2016·山东·高考真题）在△ABC中，角A，B，C的对边分别为a，b，c.已知2(tanA＋tanB)＝.
(1)证明：a＋b＝2c；
(2)求cs C的最小值．
21．（2016·四川·高考真题）在△ABC中，角A,B,C所对的边分别是a,b,c,且.
（Ⅰ）证明：；
（Ⅱ）若，求.
22．（2016·江苏·高考真题）在中，AC=6，
（1）求AB的长；
（2）求的值.
23．（2015·江苏·高考真题）在中，已知.
（1）求的长；
（2）求的值.
24．（2015·天津·高考真题）在中，内角所对的边分别为，已知的面积为．
(1) 求和的值；
(2) 求的值．
25．（2015·四川·高考真题）如图，A，B，C，D为平面四边形ABCD的四个内角.
（1）证明：
（2）若求的值.
26．（2015·湖南·高考真题）设的内角的对边分别为.
（Ⅰ）证明：；
（Ⅱ）若，且为钝角，求.
27．（2015·湖南·高考真题）设的内角，，的对边分别为，，，，且为钝角. （1）证明：； （2）求的取值范围.
28．（2015·全国·高考真题）△ABC中D是BC上的点,AD平分BAC,BD=2DC．
（Ⅰ）求 ；
（Ⅱ）若,求.
考点04 求三角形的高、中线、角平分线及其他线段长
1．（2023·全国新Ⅰ卷·高考真题）已知在中，．
(1)求；
(2)设，求边上的高．
2．（2018·北京·高考真题）在中，．
（1）求；
（2）求边上的高．
3．（2018·全国·高考真题）在平面四边形中，，，，.
（1）求；
（2）若，求.
4．（2015·安徽·高考真题）在中，,点D在边上，，求的长.
5．（2015·全国·高考真题）中，D是BC上的点，AD平分∠BAC，面积是面积的2倍．
(1)求；
(2)若AD＝1，DC＝，求BD和AC的长．
考点05 三角形中的证明问题
1．（2022·全国乙卷·高考真题）记的内角A，B，C的对边分别为a，b，c﹐已知．
(1)若，求C；
(2)证明：
2．（2021·全国新Ⅰ卷·高考真题）记是内角，，的对边分别为，，.已知，点在边上，.
（1）证明：；
（2）若，求.
3．（2016·四川·高考真题）在ABC中，角A，B，C所对的边分别是a，b，c，且.
（Ⅰ）证明：sinAsinB=sinC；
（Ⅱ）若，求tanB．
4．（2016·浙江·高考真题）在ABC中，内角所对的边分别为a，b，c.已知b+c=2acs B.
（Ⅰ）证明：A=2B；
（Ⅱ）若cs B=，求cs C的值．
5．（2016·山东·高考真题）在△ABC中，角A，B，C的对边分别为a，b，c.已知2(tanA＋tanB)＝.
(1)证明：a＋b＝2c；
(2)求cs C的最小值．
6．（2016·四川·高考真题）在△ABC中，角A,B,C所对的边分别是a,b,c,且.
（Ⅰ）证明：；
（Ⅱ）若，求.
7．（2015·湖南·高考真题）设的内角的对边分别为.
（Ⅰ）证明：；
（Ⅱ）若，且为钝角，求.
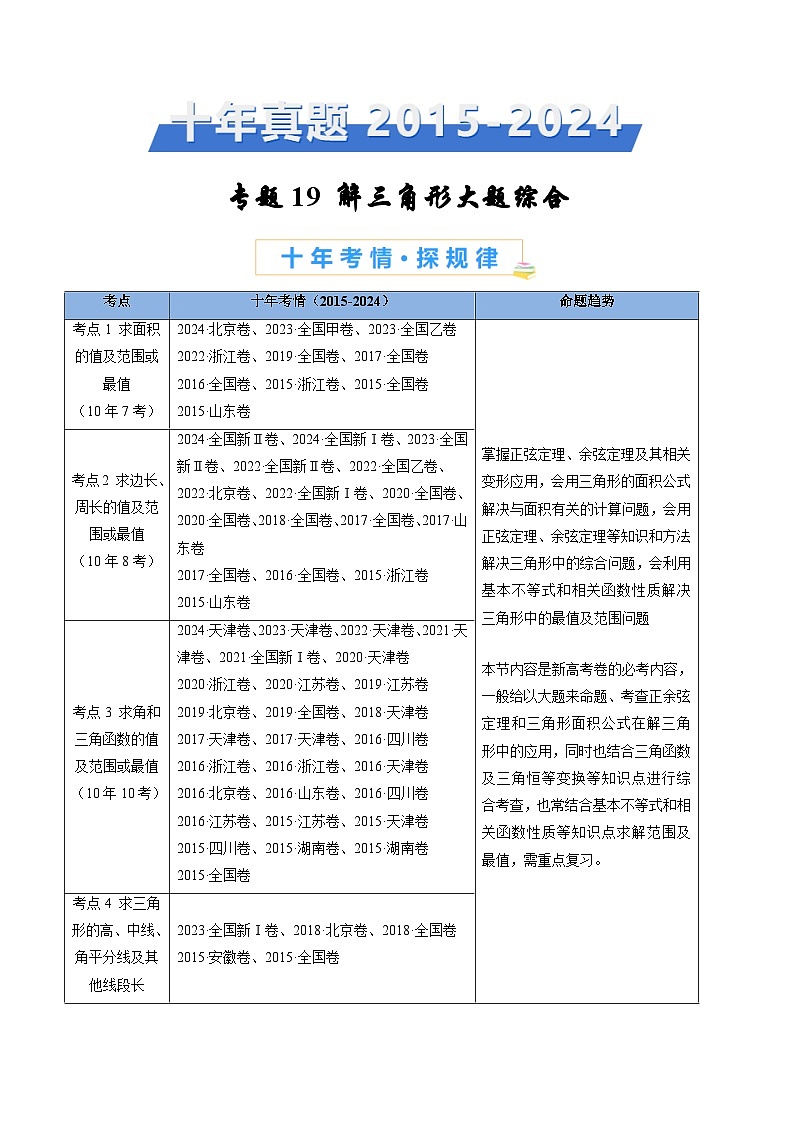
考点
十年考情（2015-2024）
命题趋势
考点1 求面积的值及范围或最值
（10年7考）
2024·北京卷、2023·全国甲卷、2023·全国乙卷
2022·浙江卷、2019·全国卷、2017·全国卷
2016·全国卷、2015·浙江卷、2015·全国卷
2015·山东卷
掌握正弦定理、余弦定理及其相关变形应用，会用三角形的面积公式解决与面积有关的计算问题，会用正弦定理、余弦定理等知识和方法解决三角形中的综合问题，会利用基本不等式和相关函数性质解决三角形中的最值及范围问题
本节内容是新高考卷的必考内容，一般给以大题来命题、考查正余弦定理和三角形面积公式在解三角形中的应用，同时也结合三角函数及三角恒等变换等知识点进行综合考查，也常结合基本不等式和相关函数性质等知识点求解范围及最值，需重点复习。
考点2 求边长、周长的值及范围或最值
（10年8考）
2024·全国新Ⅱ卷、2024·全国新Ⅰ卷、2023·全国新Ⅱ卷、2022·全国新Ⅱ卷、2022·全国乙卷、2022·北京卷、2022·全国新Ⅰ卷、2020·全国卷、2020·全国卷、2018·全国卷、2017·全国卷、2017·山东卷
2017·全国卷、2016·全国卷、2015·浙江卷
2015·山东卷
考点3 求角和三角函数的值及范围或最值
（10年10考）
2024·天津卷、2023·天津卷、2022·天津卷、2021·天津卷、2021·全国新Ⅰ卷、2020·天津卷
2020·浙江卷、2020·江苏卷、2019·江苏卷
2019·北京卷、2019·全国卷、2018·天津卷
2017·天津卷、2017·天津卷、2016·四川卷
2016·浙江卷、2016·浙江卷、2016·天津卷
2016·北京卷、2016·山东卷、2016·四川卷
2016·江苏卷、2015·江苏卷、2015·天津卷
2015·四川卷、2015·湖南卷、2015·湖南卷
2015·全国卷
考点4 求三角形的高、中线、角平分线及其他线段长
（10年几考）
2023·全国新Ⅰ卷、2018·北京卷、2018·全国卷
2015·安徽卷、2015·全国卷
考点5 三角形中的证明问题
（10年4考）
2022·全国乙卷、2021·全国新Ⅰ卷、2016·四川卷
2016·浙江卷、2016·山东卷、2016·四川卷
2015·湖南卷