高教版（2021·十四五）2.1 不等式的基本性质评优课ppt课件

这是一份高教版（2021·十四五）2.1 不等式的基本性质评优课ppt课件，共32页。PPT课件主要包含了实数的大小，不等式的性质，性质1的证明等内容，欢迎下载使用。

与相等关系相比，不等关系在现实世界中更为普遍．
不等式就是描述不等关系的一种重要的数学表示形式．
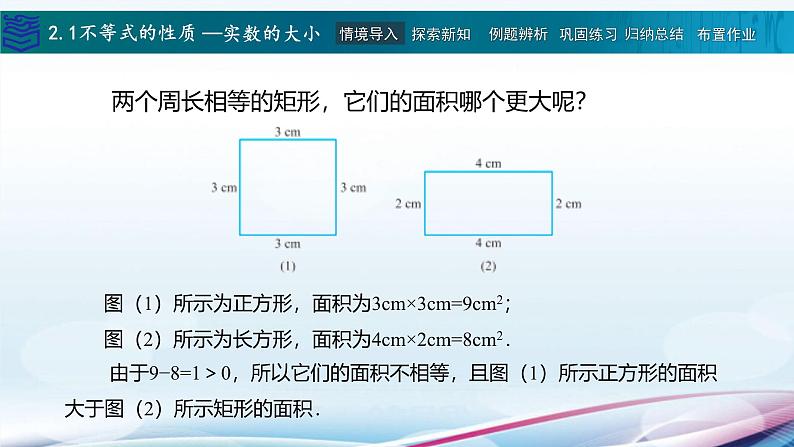
两个周长相等的矩形，它们的面积哪个更大呢？
图（1）所示为正方形，面积为3cm×3cm=9cm2；
图（2）所示为长方形，面积为4cm×2cm=8cm2．
由于9−8=1＞0，所以它们的面积不相等，且图（1）所示正方形的面积大于图（2）所示矩形的面积．
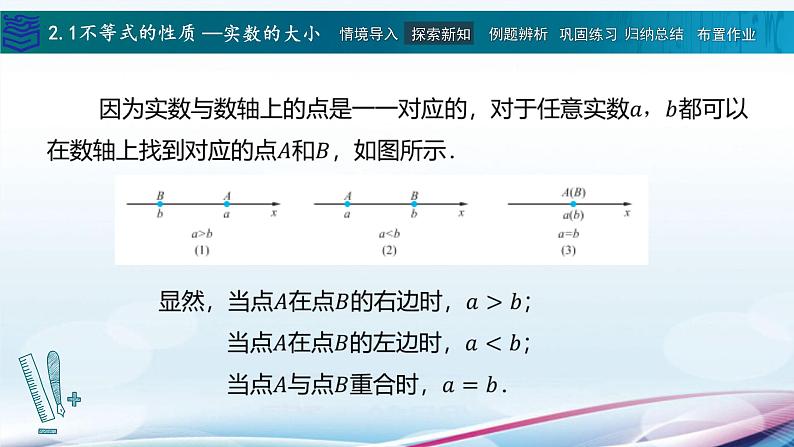
要比较两个实数（或代数式）的大小，可以转化为比较它们的差与 的大小．这种比较大小的方法称为作差比较法．
1.比较下列各组实数的大小．
比较两个实数大小的作差比较法为研究不等式奠定了基础．那么，如何用这个方法研究不等式的性质呢？
性质1表明，不等式两边同时加上（或减去）同一个数（或代数式），不等号的方向不变．因此性质1也称为不等式的加法法则．
这表明，不等式的任何一项可以从不等式的一边移到另一边，但同时要改变符号．这条结论也称为移项法则．
性质2表明，不等式两边同时乘(或除以)同一个正数，不等号的方向不变；不等式两边同时乘(或除以)同一个负数，不等号的方向改变．
性质2也称为不等式的乘法法则．
由a＞b知，a– b＞0，
于是 (a＋c)–(b＋c)=a＋c–b–c=a–b＞0，
证明 由a＞b， b＞c ，得a– b＞0，b−c＞0；
所以 a－c＝a−b＋b−c＝(a −b)＋(b −c)＞0，
性质3表明不等式具有传递性．
性质4也称为同向不等式的可加性．
证明 由a＞b， c＞d ，由性质1得
例3 用符号 填空，并说明利用了不等式的哪（几）条基本性质．
1．已知a＞b，用符号“＞”或“＜”填空:（1）a+1 b+1；（2）-5a -5b； （3）3a+3 3b+2．
1.书面作业：完成课后习题和数学学习指导与练习；2.查漏补缺：根据个人情况对课堂学习复习回顾；3.拓展作业：阅读教材扩展延伸内容．