




初中数学青岛版(2024)九年级上册3.2 确定圆的条件优质课件ppt
展开学习目标:1通过实例体会反证法的含义,知道反证法证明命题的一般步骤,能用反证法进行简单的推理证明.2.借助实例感受反证法的思想,在学习活动中,培养学生自主探究、合作交流的意识.3.反证法的证明步骤.能用反证法进行推理证明.
重点:理解反证法的证明步骤,并掌握它的运用.
难点:能用反证法进行推理证明.
王戎7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动。伙伴问他为什么不去摘?
王戎回答说:“树在道边而多子,此必苦李。”小伙伴摘取一个尝了一下果然是苦李。
王戎是怎样知道李子是苦的呢?他运用了怎样的推理方法?
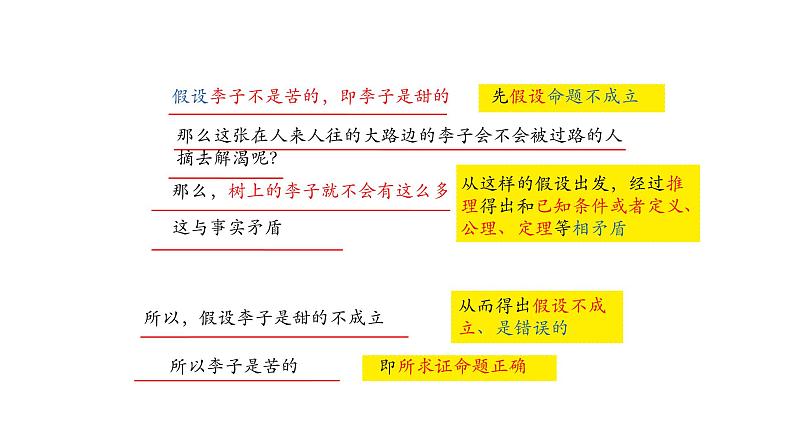
假设李子不是苦的,即李子是甜的
那么这在人来人往的大路边的李子会不会被过路的人摘去解渴呢?
那么,树上的李子就不会有这么多
所以,假设李子是甜的不成立
过在同一直线上的三点能作出一个圆吗?
为什么过同一条直线上的三点不能作圆?怎样证明这个结论呢?
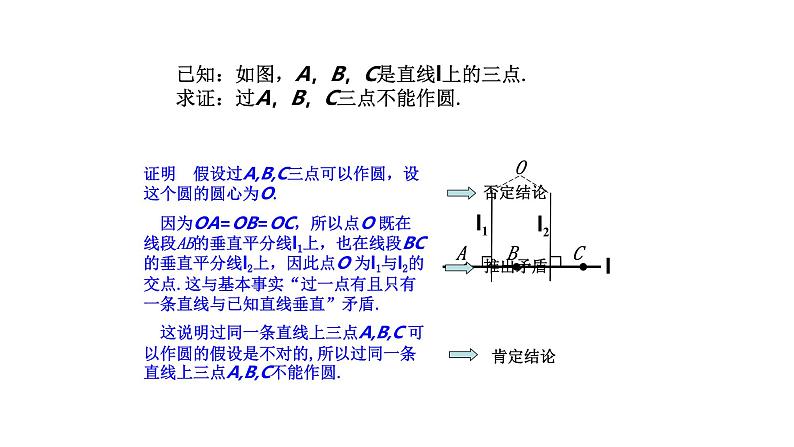
已知:如图,A,B,C是直线l上的三点.求证:过A,B,C三点不能作圆.
证明 假设过A,B,C三点可以作圆,设这个圆的圆心为O. 因为OA=OB=OC,所以点O 既在线段AB的垂直平分线l1上,也在线段BC的垂直平分线l2上,因此点O 为l1与l2的交点.这与基本事实“过一点有且只有一条直线与已知直线垂直”矛盾. 这说明过同一条直线上三点A,B,C 可以作圆的假设是不对的,所以过同一条直线上三点A,B,C不能作圆.
在证明一个命题时,人们有时候
从这样的假设出发,经过推理得出和已知条件或者定义、公理、定理等相矛盾
从而得出假设不成立、是错误的
这种证明方法叫做反证法
那么这张在人来人往的大路边的李子会不会被过路的人摘去解渴呢?
1.用反证法证明时,否定的是命题的结论,而不是 否定已知条件.2.适合用反证法的命题类型:(1)结论以否定形式出现的命题,如钝角三角形中不 能有两个钝角;(2)唯一性命题,如两条直线相交只有一个交点;(3)结论以“至多”“至少”等形式叙述的命题,如一个 凸多边形中至多有3个锐角.
3.常用的互为否定的表述方式:
是—— 存在—— 平行——垂直—— 等于—— 都是——大于—— 小于——至少有一个—— 至少有三个——至少有n个—— 至多有一个——三角形中最多有一个是直角——
三角形中有两个或三个角是直角
例1(1). 用反证法证明“在同一平面内,若a⊥c,b⊥c,则 a∥b”,第一步应假设( ) A.a∥b B.a与b垂直 C.a与b不一定平行 D.a与b相交(2).用反证法证明命题“如果x>y,那么x3>y3”时,假 设的内容应是( ) A.x3=y3 B.x3<y3 C.x3<y3或x3=y3 D.x3<y3且x3=y2
证明:假设∠1≠ ∠2 过点G作直线A′B′,使∠EGB′= ∠2.根据基本事实“两条直线被第三条直线所截,如果同位角相等,那么两直线平行”,可得A′B′ ∥CD.这样,过点G就有两条直线AB与 A′B′与直线CD平行.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”矛盾. 这说明 ∠1≠ ∠2的假设是不对的,所以∠1= ∠2.
例2 证明平行线的性质定理1:两条平行线被第三条直线所截,同位角相等.
已知:如图,直线AB∥CD,直线EF与AB,CD分别相交于点G,H.求证:∠1= ∠2
证明:假设a与b不平行,则可设它们相交于点A. 那么过点A 就有两条直线a、b与直线c平行,这与“过直线外一点有且只有一条直线与已知直线平行”矛盾,假设不成立. ∴a//b.
例3 已知:如图有a、b、c三条直线,且a//c,b//c. 求证:a//b
假设这个三角形是等腰三角形
4. 在△ABC中,AB≠AC,求证:∠B≠∠C
证明:假设 则 ( )这与 矛盾.假设不成立。∴ .
【归纳】反证法的步骤: 假设结论的反面成立→逻辑推理得出矛盾→肯定原结论正确。
5.用反证法证明:若a,b,c是不全为0的实数,且 a+b+c=0,那么a,b,c这三个数中至少有一个负数.证明:假设a,b,c都不是________, ∵ a,b,c不全为0, ∴ a,b,c中至少有一个为正数, ∴ a+b+c________0,这与已知相________, ∴______________,原命题成立, 即a,b,c这三个数中至少有一个负数.
6.用反证法证明:等腰三角形的底角必定是锐角。
已知:在△ABC中,AB=AC.求证:∠B、∠C为锐角。
证明:假设∠B≥ 90°, ∠C ≥90°则∠A+∠B+∠C>180°,这与三角形内角和定理矛盾∴假设不成立.故原命题正确∴等腰三角形的底角必定是锐角.
7.已知:如图,在△ABC中,AB=AC,∠APB≠∠APC. 求证:PB≠PC
证明:假设PB=PC在△ABP与△ACP中 AB=AC(已知) AP=AP(公共边) PB=PC(已知)∴△ABP≌△ACP(SSS)∴∠APB=∠APC这与已知条件∠APB≠∠APC矛盾假设不成立.∴PB≠PC
8.用反证法证明在一个三角形中,不能有两个角是钝角.
解:已知:∠A,∠B,∠C是三角形ABC的三个内角. 求证:∠A,∠B,∠C中不能有两个钝角. 证明:假设∠A,∠B,∠C中有两个钝角,不妨 设∠A>90°,∠B>90°,则∠A+∠B+∠C> 180°,这与三角形的内角和定理相矛盾. 故 ∠A, ∠B均大于90°不成立. 所以,在一个三角形中不能有两个钝角.
已知:△ABC求证:△ABC中至少有一个内角小于或等于60°.
证明:假设 则 ∴即 这与 矛盾.假设不成立.∴ .
△ABC中没有一个内角小于或等于60°
∠A>60°,∠B>60°,∠C>60°
∠A+∠B+∠C > 180°
三角形的内角和为180度
△ABC中至少有一个内角小于或等于60°
∠A+∠B+∠C > 60°+60°+60°=180°
9. 求证:在一个三角形中,至少有一个内角小于或等于60°.
美国总统华盛顿从小非常聪明,小偷凡劲鲍克家偷走了许多东西,根据迹象表明小偷就是本村人,华盛顿灵机一动对本村人讲起了故事:“黄蜂是上帝的使者,能辨别人间的真假。”忽然华盛顿大声喊道:“小偷就是他,黄蜂正在他的帽子上兜圈子,要落下来了!”大家回头张望,看着那个想把帽子上黄蜂赶走的人,其实哪有什么黄蜂?华盛顿大喝一声:“小偷就是他!”
你知道华盛顿是如何推理的么?
数 学 活 动 室
故事说一个少妇抱着小孩回娘家,路过瓜田,遇上一个恶少调戏。少妇不从,被诬偷瓜,告到县衙。恶少暗中用 钱收买为他看瓜的地保,嘱他摘三个大瓜到县衙作证。张飞升堂审讯,问恶 少,恶少说少妇偷他的瓜,有人证物证;问少妇,少妇说恶少调戏她。张飞 “想了一想”,佯断少妇偷瓜,命恶少先把三个大瓜 抱回去。恶少左抱右抱,怎么也抱不起来。张飞虎眉一 竖,拍案而起,痛斥恶少"你堂堂男子汉,三个瓜都 抱不动,她是弱女子, 又抱小孩,怎能偷你三个大 瓜?分明是你调戏。"经过审问,果然不错。
你知道张飞是如何推理的么?
初中数学青岛版(2024)九年级上册3.2 确定圆的条件优秀作业课件ppt: 这是一份初中数学青岛版(2024)九年级上册<a href="/sx/tb_c75359_t3/?tag_id=26" target="_blank">3.2 确定圆的条件优秀作业课件ppt</a>,共23页。PPT课件主要包含了课堂导入,探究新知,课堂练习等内容,欢迎下载使用。
初中数学青岛版(2024)九年级上册3.2 确定圆的条件优秀作业ppt课件: 这是一份初中数学青岛版(2024)九年级上册<a href="/sx/tb_c75359_t3/?tag_id=26" target="_blank">3.2 确定圆的条件优秀作业ppt课件</a>,文件包含32确定圆的条件第1课时分层作业解析版docx、32确定圆的条件第1课时分层作业原卷版docx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。
初中数学青岛版九年级上册2.4 解直角三角形精品课件ppt: 这是一份初中数学青岛版九年级上册<a href="/sx/tb_c99060_t3/?tag_id=26" target="_blank">2.4 解直角三角形精品课件ppt</a>,共15页。PPT课件主要包含了课堂导入,转化思想,探究新知,练一练3,课堂练习等内容,欢迎下载使用。














