内蒙古自治区乌兰察布市第三中学2023-2024学年九年级上学期期末数学试题(含解析)

这是一份内蒙古自治区乌兰察布市第三中学2023-2024学年九年级上学期期末数学试题(含解析)，共24页。试卷主要包含了选择题．，填空题．，解答题．等内容，欢迎下载使用。

九年级数学
分值：120分 时间：120分钟
一、选择题．（每题只有一个正确答案，请将正确答案填在下面的表格里．每题3分，共30分）
1．下列函数中，y是x的反比例函数的是（ ）
A．B．C．D．
2．在数学活动课中，同学们利用几何画板绘制出了下列曲线，其中是中心对称图形的是（ ）

A．等角螺旋线B．心形线C．四叶玫瑰线D．蝴蝶曲线
3．下列事件是不可能事件的是（ ）
A．太阳从东方升起B．三条线段组成一个三角形
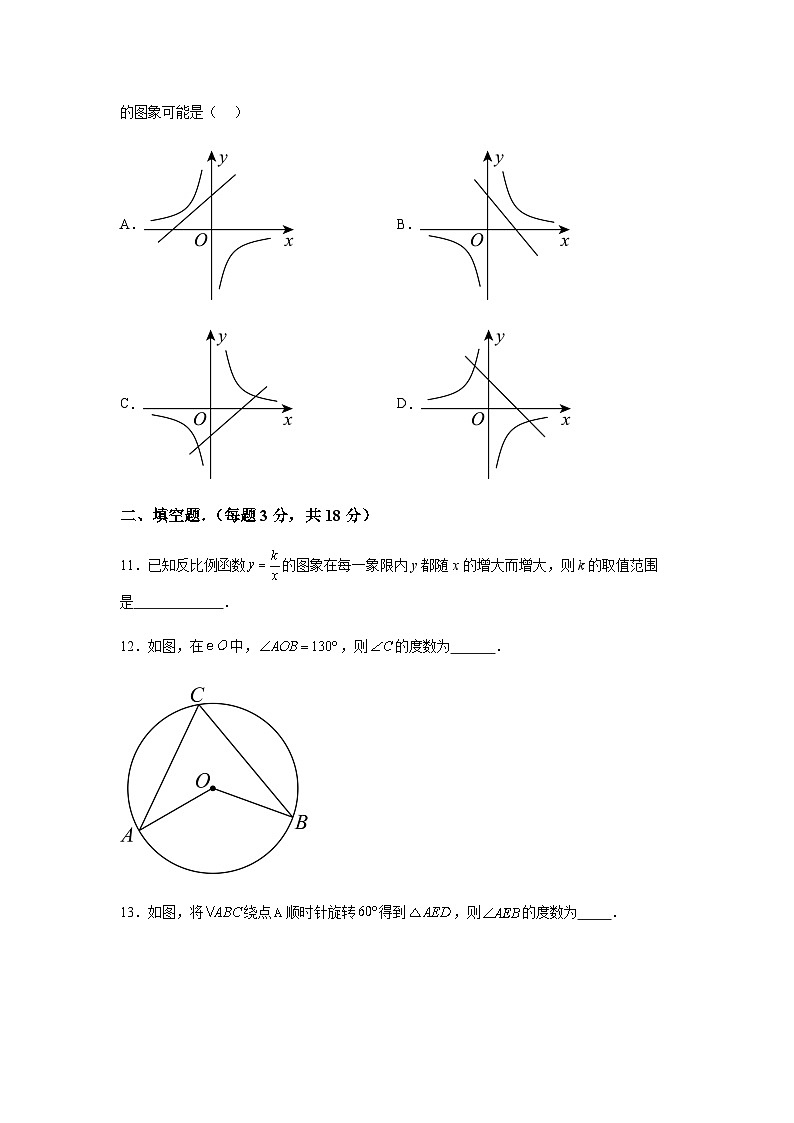
C．（为实数）D．购买一张大乐透，中奖500万
4．下列各点在反比例函数图象上的是（ ）
A．B．C．D．
5．关于的方程的根的情况判断正确的是（ ）
A．有两个不相等的实数根B．有两个相等的实数根
C．无实数根D．有一个实数根
6．正六边形的中心角为（ ）
A．B．C．D．
7．已知蓄电池的电压为定值，使用蓄电池时，电流（单位：A）与电阻（单位：）是反比例函数关系．下列反映电流与电阻之间函数关系的图象大致是（ ）
A． B． C． D．
8．圆锥的底面圆的半径为1，母线长为3，则它的侧面展开图的圆心角度数为（ ）
A．B．C．D．
9．一位同学在画二次函数的图象时，把看成了，结果所画图像是由原图象向左平移6个单位长度所得的图象，则b的值为（ ）
A．24B．C．D．12
10．一次函数与反比例函数（a，b为常数且均不等于0）在同一坐标系内的图象可能是（ ）
A． B．
C． D．
二、填空题．（每题3分，共18分）
11．已知反比例函数的图象在每一象限内y都随x的增大而增大，则k的取值范围是 ．
12．如图，在中，，则的度数为 ．

13．如图，将绕点顺时针旋转得到，则的度数为 ．
14．已知点，在反比例函数的图象上，且，则的值为 （填“正数”或“负数”或“0”）．
15．小华酷爱足球运动一次训练时，他将足球从地面向上踢出，足球距地面的高度（单位：）与足球被踢出后经过的时间（单位：）之间的关系为：，则足球距离地面的最大高度为 m．
16．如图，点A在x轴的负半轴上，点C在反比例函数的图象上，交y轴于点B，若点B是的中点，的面积为，则k的值为 ．
三、解答题．（本大题7个小题，共72分）
17．（1）解方程：；
（2）如图，在平面直角坐标系中，的三个顶点坐标分别为，，，在坐标系中画出关于原点对称的，并写出点、的坐标．
18．已知变量y与x成反比例函数关系，其部分对应数值如表格所示：
(1)求y与x的函数关系式，及表中a的值；
(2)根据表格中对应数值，在所给坐标系上画出该反比例函数在第一象限上的图象．
19．某校团支部组织部分共青团员开展学雷锋志愿者服务活动，每个志愿者都可以从以下三个项目中任选一项参加：①敬老院做义工；②文化广场地面保洁；③路口文明岗值勤．
(1)小明选择项目①的概率为___________；
(2)用画树状图或列表的方法求小明和小慧选择参加同一项目的概率．
20．如图，一次函数与反比例函数的图象交于点，．
(1)求反比例函数和一次函数的表达式；
(2)连接、，求的面积．
21．如图，以的边为直径作，交边于点D，为的切线，弦于点F，连接．
(1)求证：．
(2)若点F为中点，且，求线段的长．
22．某文具店购进一批纪念册，每本进价为20元，在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系：．
(1)当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是多少元？
(2)设该文具店每周销售这种纪念册所获得的利润为w元，将该纪念册销售单价定为多少元时，才能使文具店销售该纪念册所获利润最大？最大利润是多少？
23．如图，在平面直角坐标系中，二次函数的图象与x轴交于点，，与y轴交于点C．
(1)填空： ， ；
(2)若点D为第四象限内抛物线上的一个动点，过点D作轴交于点E，过点D作于点F，过点F作轴于点G，求出的最大值及此时点D的坐标．
参考答案与解析
1．D
【分析】本题考查了反比例函数的定义，根据反比例函数的解析式判断即可．
【详解】解：反比例函数的解析式的形式为：且k为常数，因而可知选项D是反比例函数，其余选项均不是反比例函数．
故选：D．
2．C
【分析】本题主要考查了中心对称图形的定义，熟练掌握一个平面图形，绕一点旋转，与自身完全重合，此平面图形为中心对称图形，是解题的关键．
根据中心对称图形的定义，对选项逐个判断即可．
【详解】解：对于A选项，不是中心对称图形，不符合题意；
对于B选项，不是中心对称图形，不符合题意；
对于C选项，是中心对称图形，符合题意；
对于D选项，不是中心对称图形，不符合题意；
故选：C．
3．C
【分析】此题考查了不可能事件、随机事件、必然事件，解题的关键是熟悉随机事件、必然事件的概念．根据不可能事件、随机事件、必然事件概念对选项进行判断即可．
【详解】解：A．太阳从东方升起是必然事件；
B．三条线段组成一个三角形是随机事件；
C．∵，故（为实数）是不可能事件；
D．购买一张大乐透，中奖500万，是随机事件；
故选：C．
4．B
【分析】本题主要考查反比例函数图象上点的坐标特征，根据反比例函数解析式可得，然后对各选项分析判断即可得解．
【详解】解：∵
∴
A.，该选项错误；
B. ，该选项正确；
C. ，该选项错误；
D. ，该选项错误.
故答案选：B.
5．A
【分析】本题考查根的判别式．根据题意利用与0比较即可得到本题答案．
【详解】解：，
∵，
∴，
∵，
∴方程有两个不相等的实数根，
故选：A．
6．C
【分析】本题考查了正多边形中心角定义．根据题意正多边形中心角即为除以正多边形边数即可选出本题答案．
【详解】解：∵是正六边形，
∴中心角为：，
故选：C．
7．D
【分析】根据电流与电阻之间函数关系可知图象为双曲线，并且在第一象限，即可得到答案．
【详解】∵反比例函数的图象是双曲线，且，，
∴图象是第一象限双曲线的一支．
故选：D．
【点睛】本题考查了反比例函数的图象，并结合实际意义去判断图象，数形结合思想是关键．
8．C
【分析】本题考查了求圆锥侧面展开图的圆心角，熟练掌握弧长公式是解题关键．
【详解】解：设圆锥的侧面展开图的圆心角度数为，
根据题意有：，
解得：，
故选：C
9．D
【分析】本题考查的是二次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．
利用二次函数平移规律 “上加下减，左加右减”的原则结合对称轴的性质进行解答即可．
【详解】解：二次函数的图象的对称轴为，
把看成了，
所画图象的对称轴为，
两条对称轴关于y轴对称，
所画图像是由原图象向左平移6个单位长度所得的图象，
，即．
故选D．
10．D
【分析】先根据一次函数图象确定a、b的符号，进而求出的符号，由此可以确定反比例函数图象所在的象限，看是否一致即可．
【详解】解：A、∵一次函数图象经过第一、二、三象限，
∴，
∴，
∴反比例函数的图象见过第一、三象限，这与图形不符合，故A不符合题意；
B、∵一次函数图象经过第一、二、四象限，
∴，
∴，
∴反比例函数的图象见过第二、四象限，这与图形不符合，故B不符合题意；
C、∵一次函数图象经过第一、三、四象限，
∴，
∴，
∴反比例函数的图象见过第二、四象限，这与图形不符合，故C不符合题意；
D、∵一次函数图象经过第一、二、四象限，
∴，
∴，
∴反比例函数的图象见过第二、四象限，这与图形符合，故D符合题意；
故选D．
【点睛】本题主要考查了一次函数与反比例函数图象和性质，熟练掌握相关性质与函数图象的关系是解决本题的关键．
11．
【分析】本题考查的是反比例函数的性质，根据反比例函数的图象在每一象限内y随x的增大而增大得出即可．
【详解】解:∵反比例函数的图象在每一象限内y都随x的增大而增大，
∴.
故答案为：.
12．##度
【分析】根据圆周角定理即可求解．
【详解】解：∵，，
∴，
故答案为：．
【点睛】本题考查了圆周角定理，熟练掌握圆周角定理是解题的关键．
13．
【分析】本题考查了旋转的性质，等边三角形的判定与性质，主要利用了旋转前后对应边相等以及旋转角的定义．证等边三角形是本题的关键．
由旋转的性质可得，，可证是等边三角形，即可求出答案．
【详解】绕点A顺时针旋转得到，
，，
，
即，
是等边三角形
故答案为：
14．正数
【分析】本题考查了根据反比例函数的增减性比较反比例函数值或自变量的大小；对于反比例函数，当时，图象在一、三象限均有随的增大而减小；当时，图象在二、四象限均有随的增大而增大．据此即可求解．
【详解】解：∵对于反比例函数，，
∴图象在一、三象限均有随的增大而减小
∵，
∴
∴的值为正数
故答案为：正数
15．9
【分析】本题考查了二次函数的图象和性质，利用二次函数求最值，解题的关键是熟悉二次函数的性质，即顶点的纵坐标是函数的最值；
开口方向向下，最大值为顶点坐标纵坐标，由公式可得答案．
【详解】
，，，
足球距离地面的最大高度为抛物线的顶点坐标的纵坐标，
函数的对称轴为：，
当时，h最大，
将代入中得，
故答案为：9
16．6
【分析】根据全等三角形的判定和性质以及三角形的面积公式可得，进而得出，由系数k的几何意义可得答案．
【详解】解：如图，过点C作轴于D，
∴，
∵点B是的中点，
∴，
在和中，
，
∴，
∴，
∴，
∴，
∴，
∴，
∵，
∴．
故答案为：6．
【点睛】本题考查反比例函数系数k的几何意义以及全等三角形的判定和性质，理解反比例函数系数k的几何意义，掌握全等三角形的判定和性质是正确解答的前提．
17．（1），；（2）画图见解析，，
【分析】本题考查了一元二次方程的解法，中心对称的作图，关于原点对称的两点的坐标特点等知识，
（1）利用因式分解法解一元二次方程即可；
（2）根据关于原点对称的两点横纵坐标互为相反数，先求出三个顶点的坐标，然后描点连线即可．
【详解】（1）
∴或
解得，；
（2）如图所示，即为所求；
∴，．
18．(1)，a的值为3
(2)见解析
【分析】（1）设y与x成反比例函数关系式为y（k≠0），再将（1，6）代入即可求出k，把x＝2代入关系式可求出a；
（2）描点，连线即可．
【详解】（1）设y与x成反比例函数关系式为y（k≠0），
由表格中的数据可知，当x＝1时，y＝6，
∴6，解得k＝6，
∴y与x成反比例函数关系式为y，
当x＝2时，y3，即a的值为3．
（2）根据表格中的数据在坐标系上画出函数图象（x＞0），如下图所示：
【点睛】本题考查的是反比例函数的定义，即形如y（k≠0）的函数称为反比例函数．
19．(1)
(2)小明和小慧选择参加同一项目的概率是
【分析】本题考查了概率公式，画树状图，根据题意画出树状图是解题的关键．
（1）直接根据概率的计算公式进行计算即可；
（2）根据题意画出树状图，然后再根据概率的计算公式进行计算即可．
【详解】（1）解：从三个项目中任选一项，小明选择项目①的概率为，
故答案为：；
（2）解：画树状图如下：
，
∵共有种等可能的情况，其中小明和小慧选择参加同一项目的有种情况，
∴小明和小慧选择参加同一项目的概率是，
故答案为：．
20．(1)，
(2)8
【分析】本题主要考查一次函数以反比例函数的综合，掌握待定系数法求解析式，几何图形面积的计算方法是解题的关键．
（1）用待定系数法求解析式即可求解；
（2）如图所示，过点A作轴于点D，过点B作轴于点E，根据几何图形面积的计算方法，图形结合即可求解．
【详解】（1）解：（1）∵点在的图象上，
代入得：，
∴反比例函数的表达式为，
∵点在的图象上，
∴，
，
将，代入中，
得：，解得：，
∴一次函数的表达式为.
（2）解：把代入得：，
∴，如图所示，过点A作轴于点D，过点B作轴于点E，
∴．
21．(1)见解析
(2)
【分析】本题考查了切线的定义，圆周角定理，垂径定理，熟练掌握相关性质定理，正确作出辅助线，构造直角三角形，是解题的关键．
（1）根据切线的定义得出，进而得出，则，根据圆周角定理得出，即可求证；
（2）根据中点的定义得出，则，再根据勾股定理得出，最后根据垂径定理得出，即可求解．
【详解】（1）证明：∵为的切线，
∴，
∵，
∴，
∴，
∵，
∴；
（2）解：连接，
∵点F为中点，且，
∴，
∴，
根据勾股定理可得：，
∵，
∴．
22．(1)25元或35元
(2)当该纪念册销售单价定为30元时，才能使该纪念册所获利润最大，最大利润为200元
【分析】本题考查一元二次方程和二次函数的应用，根据题意找出等量关系并列出方程或解析式是解题的关键．
（1）根据题意，利用单本利润乘以销售数量等于总利润列方程求解即可；
（2）根据题意，利用单本利润乘以销售数量等于总利润列函数解析式，再化成顶点式即可得解．
【详解】（1）解：依题意得：，
解得：，，
每本纪念册的销售单价为25元或35元，
（2）由题意得：
，
，即开口向下，
当时，w有最大值，最大值为200，
当该纪念册销售单价定为30元时，才能使该纪念册所获利润最大，最大利润为200元．
23．(1)，
(2)有最大值，
【分析】本题考查待定系数法求解函数解析式和二次函数的综合应用，熟练掌握二次函数的图象及性质是解题的关键．
（1）将点，代入，即可求解；
（2）延长交x轴于点K，延长交于点H，设，，进而得出， ，，由二次函数的性质可得有最大值，进而可求出点D的坐标．
【详解】（1）解：将点，代入得：
，
解得：
故答案为：，；
（2）解：延长交x轴于点K，延长交于点H，如图1，
令，则，
，
设直线的解析式为，
将点，代入可得：，
解得：，所以，
设，则，
，
，
，
，
，
，
，
，
当时，有最大值，
此时．
x
…
1
2
3
4
6
…
y
…
6
a
2
1.5
1
…