中职数学高教版（2021）基础模块上册第3章 函数3.2 函数的表示方法公开课ppt课件

这是一份中职数学高教版（2021）基础模块上册第3章 函数3.2 函数的表示方法公开课ppt课件，文件包含课件高教版2021数学基础模块上册32《函数的表示方法》课件pptx、函数的表示方法mp4等2份课件配套教学资源，其中PPT共21页， 欢迎下载使用。

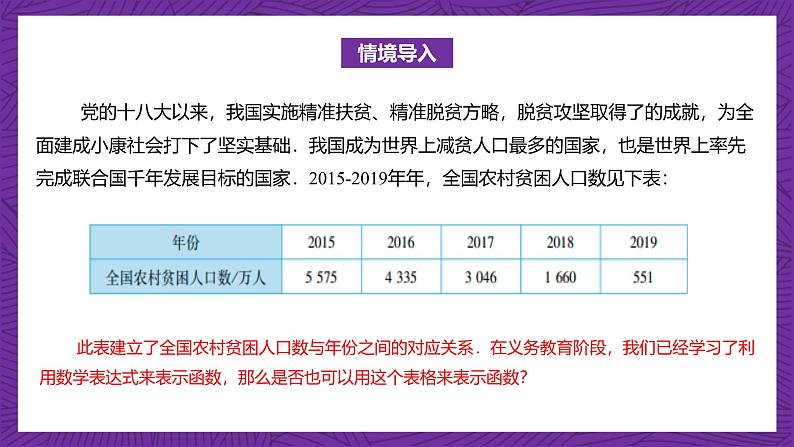
党的十八大以来，我国实施精准扶贫、精准脱贫方略，脱贫攻坚取得了的成就，为全面建成小康社会打下了坚实基础．我国成为世界上减贫人口最多的国家，也是世界上率先完成联合国千年发展目标的国家．2015-2019年年，全国农村贫困人口数见下表：
此表建立了全国农村贫困人口数与年份之间的对应关系．在义务教育阶段，我们已经学习了利用数学表达式来表示函数，那么是否也可以用这个表格来表示函数？
回顾学过的知识，除了表达式、列表，我们还有其他的方式来表示函数吗？函数的表示方法有几种？
像这样利用解析式表示函数的方法称为解析法．
如义务教育阶段学习的一次函数、一元二次函数、反比例函数等都是用解析法表示的．
网购已经成为人们日常生活的一部分.某电商平台从2009年至 2019年, 在每年的11月11日网购促销活动中, 每年销售额情况如表所示. 清晰地反映了年份x(年)与当年销售额y(亿元)之间的对应关系.像这样通过列出自变量的值与对应函数值的相应表格来表示函数的方法称为列表法．
某便民超市促销某种小毛巾, 每条售价4元, 每人限购5条.若顾客购买x 条小毛巾需要付款y元, 用图像法表示函数y=f(x)如图所示.像这样利用图像表示函数的方法称为图像法．
3.1“ 情境与问题（3）”中的某地某天的气温与时间的对应关系也是用图像法表示的．
综上所述，函数的表示方法通常有三种： 解析法，列表法和图像法．
函数的三种表示法各自的优势与不足吗？
如果想要根据某同学五次考试成绩分析他这一学期的数学学习情况，试选择恰当的方法表示这个问题中的函数关系．
典例1 文具店内出售某种签字笔，每支售价6.5元，分别用列表法和解析法表示购买4支以内的签字笔时，应付款与签字笔支数之间的函数．
解 （1）依题意，得到应缴水费与用水量之间的关系，见下表
每户每年用水不超过180m³时，水价为5元/ m³；超过180m³不超过260m³时，超过的部分按7元/m³收费；超过260m³时，超过的部分按9元/m³收费．
由表得到函数的解析式：
(1)根据这个解析式，可以画出函数的图像．
分段函数的定义域是自变量的各段不同取值范围的并集，值域是函数在各段不同取值范围的函数值的并集．分段函数在整个定义域上仍然是一个函数，而不是几个函数．
作分段函数的图像时，在各段不同取值范围内，根据相应解析式，做出相应部分的图像．
现实生活中，有很多函数是分段描述的．如，阶梯电费、出租车费、个人所得税等．这类函数的特点是：当自变量在不同范围内取值时，需要用不同的解析式来表示，我们称这样的函数为分段函数．
【巩固1】一艘军舰与某海港相距135海里(1海里≈1.852km), 如果军舰 以每小时45海里的速度向海港前行, 则3h后可到达海港.假设这艘军舰 出发t(h)后, 与海港的距离是s海里.（1）用解析法表示函数s=f(t); (2)用图像法表示函数s=f(t).
解 (1)因为军舰从出发地驶入海港需要用时3(h), 所以函数的定义域为数集{t|0≤t≤3}. 又因为军舰出发t(h)后, 行驶的路程为45t海里, 这时军舰 与海港的距离为(135-45t)海里. 所以, 用解析法可将函数s=f(t)表示为 s=-45t+135, 0≤t≤3. 函数s=f(t)是一次函数, 用图像法可将函数表示为图
解 (1)因为-5<0, 所以f(-5)=-5+2=-3. 因为4>0, 所以f(4)=42-3=13. (2)因为-1<0, 所以f(-1)=-1+2=1. 又因为1>0, 所以f[f(-1)]=f(1)=12-3=-2.
【巩固2】某城市地铁的票价如表所示.1号线地铁全长21km.设乘坐的路 程为x(km), 票价是y(元), 则y 是x 的函数, 你能写出这个函数的解析式吗?
解：从表可以发现, 当x≤6时, y=2; 当6 巩固作业： P98练习3.2； P99习题3.2的1(填在课本上),2，3，4，5.