中职数学高教版（2021）基础模块上册4.6.1 正弦函数的图像优秀课件ppt

这是一份中职数学高教版（2021）基础模块上册4.6.1 正弦函数的图像优秀课件ppt，文件包含课件高教版2021数学基础模块上册461《正弦函数的图像》课件pptx、五点法作图mp4、简谐运动现象演示mp4等3份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

简谐运动是最基本也是最简单的机械振动． 单摆是常见的简谐振动之一，用盛沙的漏斗代替单摆，下面的薄木板被水平匀速拉出时，做简谐运动的漏斗漏出的沙在板上形成的曲线是什么样的呢？
当盛沙的漏斗下面的薄木板被水平匀速拉出时，做简谐运动的漏斗漏出的沙在板上形成的曲线是一条波浪起伏、周而复始的曲线．从前面的学习我们知道，随着角的变化，三角函数值也具有这种周而复始的变化规律．我们可以用正弦函数来刻画这条曲线．
根据单位圆的圆周运动特点, 单位圆上任意一点在圆周上旋转一周就回到原来的位置, 这说明自变量每增加或者减少2π, 正弦函数值将重复出现. 这一现象可以用公式 sin(x+2kπ) = sinx，k∈Z来表示.
一般地，对于函数 y＝f(x)，如果存在一个非零常数T，使得当x取定义域内任意一个值时，都有 f(x+T) ＝f(x)， 则称函数y＝f(x)为周期函数．非零常数T为y＝f(x)的一个周期．
如果周期函数y＝f(x)的所有周期中存在一个最小的正数 T0，那么这个最小的正数 T0就称为y＝f(x)的最小正周期．
因此正弦函数y = sinx，x∈R是一个周期函数，2π，4π，6π，…及-2π，-4π，-6π，…都是它的周期，即常数2kπ(k∈Z且k≠0)都是它的周期．
显然，2π为正弦函数的最小正周期.
本书中所涉及的周期，如果不特别说明，都是指函数的最小正周期．
(1)列表．
把区间[0,2π]分成12等份, 分别求出y=sinx在各分点及区间端点的正弦函数值.
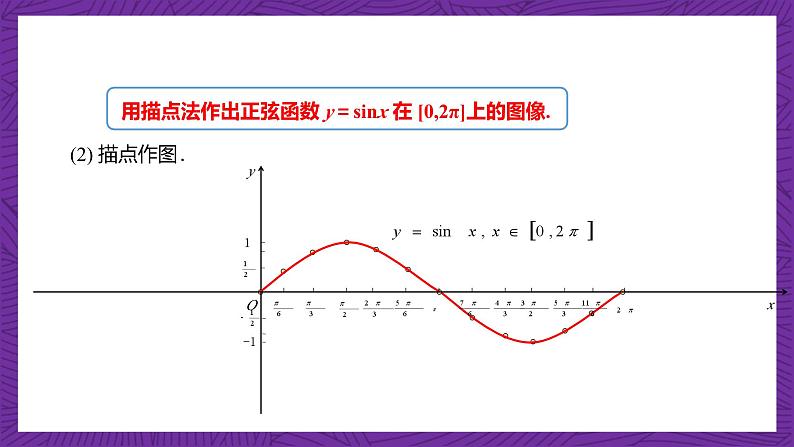
(2) 描点作图．
正弦函数y=sinx，x∈R的图像
利用图像平移得到正弦曲线
在精度要求不高时，可先描出这五个关键点，再用平滑的曲线将它们连起来，就可以得到相应区间上的正弦函数的简图.这种近似的画正弦函数的方法叫做“五点法”.
观察函数y＝sinx 在 [0,2π]上的图像发现，在确定图像的形状时，起关键作用的点有以下五个，描出这五个点后，正弦函数的图像就基本确定了.
因为正弦函数的周期是2π，所以正弦函数值每隔2π重复出现一次．于是，我们只要将函数y＝sinx在 [0,2π]上的图像沿x轴向左或向右平移2kπ(k∈Z)，就可得到正弦函数y＝sinx，x∈R的图像.正弦函数的图像也称为正弦曲线，它是一条“波浪起伏”的连续光滑曲线．
典例1 利用五点法作出函数y＝1+sinx在 [0,2π]上的图像．
根据表中x, y的数值在平面直角坐标系内描点(x,y), 再用平滑曲线顺次连接各点, 就得到函数y＝1+sinx在 [0,2π]上的图像.
y = 1- sin x , x ∈ [0,2π]
y = 2 sin x-1 , x ∈ [0,2π]
巩固作业： P186练习4. 6.1；P190习题4.6A1,1,B,2.