







人教版(2024)九年级上册22.2二次函数与一元二次方程评优课ppt课件
展开函数与方程是初中阶段的重点内容。八年级下册学生学习了一次函数,研究了一次函数与一元一次方程(二元一次方程组)的联系,本节课加深函数与方程的联系,利用二次函数研究一元二次方程,用函数的观点看方程,可以把方程看成函数值为某个定值时的情况,所以,研究函数与方程的关系是对函数的进一步深化。本章专设一节,通过探讨二次函数与一元二次方程的联系,再次展示函数与方程之间的联系。这样既深化学生对一元二次方程的认识,又可以运用二次函数解决一元二次方程的相关问题,体现了知识之间的联系。
1.通过探索,理解二次函数与一元二次方程之间的联系.2.能运用二次函数的图象与性质确定方程的解.3.了解用图象法求一元二次方程的近似根.
1.若一次函数y=kx+b的图象经过点(0,1),(1,0),则方程kx+b=0的解是___________.
2.一次函数y=kx+b的图象如图所示,则方程kx+b=-3的解是____________.
3.对于二次函数y=ax2+bx+c(a≠0),当y取一个确定值时,它就变成了一个一元二次方程,由此可知一元二次方程与二次函数有着密切的关系.那么,二次函数y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)之间到底有怎样的关系呢?
探究:以40 m /s的速度将小球沿与地面成 30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,小球的飞行高度 h (单位:m)与飞行时间 t (单位:s)之间具有关系:h= 20t–5t2 . 考虑下列问题:(1)小球的飞行高度能否达到 15 m? 若能,需要多少时间?(2)小球的飞行高度能否达到 20 m? 若能,需要多少时间?(3)小球的飞行高度能否达到 20.5 m?为什么?(4)小球从飞出到落地要用多少时间?
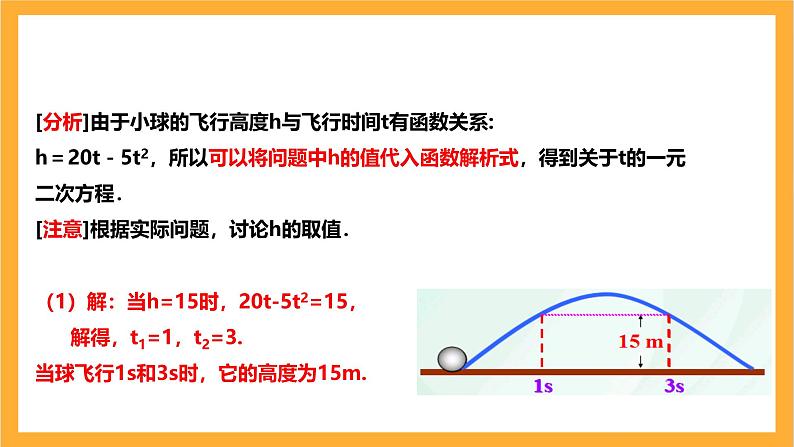
[分析]由于小球的飞行高度h与飞行时间t有函数关系:h=20t-5t2,所以可以将问题中h的值代入函数解析式,得到关于t的一元二次方程.[注意]根据实际问题,讨论h的取值.
(1)解:当h=15时,20t-5t2=15, 解得,t1=1,t2=3.当球飞行1s和3s时,它的高度为15m.
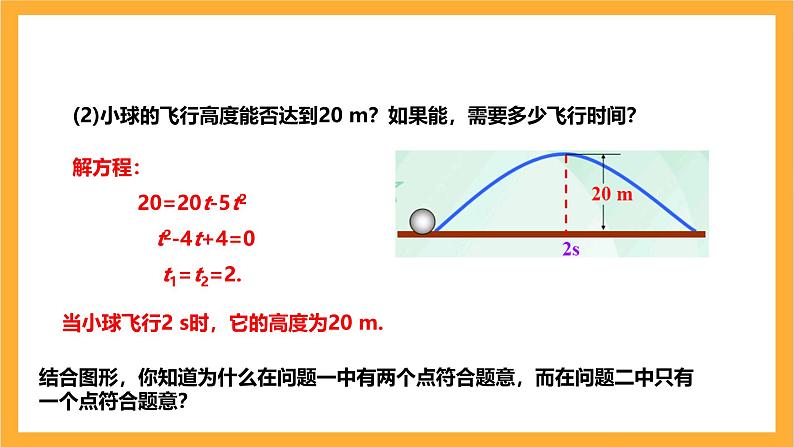
(2)小球的飞行高度能否达到20 m?如果能,需要多少飞行时间?
解方程: 20=20t-5t2 t2-4t+4=0 t1=t2=2.
当小球飞行2 s时,它的高度为20 m.
结合图形,你知道为什么在问题一中有两个点符合题意,而在问题二中只有一个点符合题意?
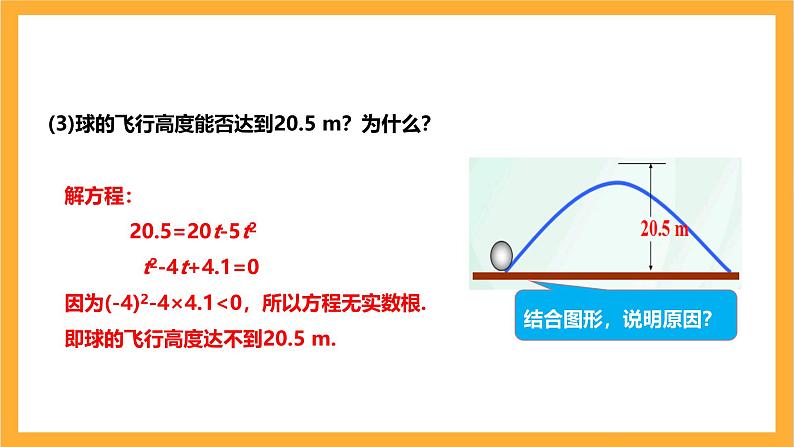
(3)球的飞行高度能否达到20.5 m?为什么?
解方程: 20.5=20t-5t2 t2-4t+4.1=0因为(-4)2-4×4.1<0,所以方程无实数根.即球的飞行高度达不到20.5 m.
(4)小球从飞出到落地要用多少时间?
解方程 0=20t-5t2 t2-4t=0 t1=0,t2=4.
当小球飞行0 s和4 s时,它的高度为0 m.这表明小球从飞出到到落地要用4 s,即0 s时小球从地面飞出,4 s时小球落回地面.
小球飞出时和落地时的高度都为0 m.
从以上可以看出:已知二次函数y的值为m,求相应自变量x的值,就是求相应一元二次方程的解.例如,已知二次函数y=-x2+4x的值为3,求自变量x的值.就是求方程3=-x2+4x的解.例如,解方程x2-4x+3=0,就是已知二次函数y=x2-4x+3的值为0,求自变量x的值.
从上面发现,二次函数y=ax2+bx+c何时为一元二次方程?
一般地,当y取定值且a≠0时,二次函数为一元二次方程.
二次函数与一元二次方程的关系:
已知二次函数,求自变量的值
观察思考下列二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?当x取公共点的横坐标时,函数的值是多少?由此你能得出相应的一元二次方程的根吗?(1)y=x2+x-2;(2)y=x2-6x+9;(3)y=x2-x+1.
二次函数y =x2+x-2,y=x2-6x+9,y =x2–x+1的图象如图所示.
x2-6x+9=0,x1=x2=3
x2+x-2=0,x1=-2,x2=1
由上述问题,你可以得到什么结论呢?
方程ax2+bx+c=0的解就是抛物线y=ax2+bx+c与x轴公共点的横坐标。当抛物线与x轴没有公共点时,对应的方程无实数根.
二次函数y=ax2+bx+c的图象与x轴的位置关系有三种:
例1 利用函数图象求方程x2-2x-2=0的实数根(结果保留小数点后一位).
解:画出y=x2-2x-2的图象
y = x2-2x-2
它与x轴的公共点的横坐标大约是-0.7,2.7.所以方程x2-2x-2=0的实数根为x1≈ -0.7,x2≈2.7.
思考:利用二次函数的图象解一元二次方程的基本步骤有哪些?
1.画出函数的图象;2.根据图象确定抛物线与x轴的交点分别在哪两个相邻的整数 之间;3.利用计算器探索其解的十分位数字,从而确定方程的近似根.
【知识技能类作业】必做题:
2.下列抛物线中,与x轴有两个交点的是( ) A.y=3x2-5x+3 B.y=4x2-12x+9 C.y=x2-2x+3 D.y=2x2+3x-4
3.二次函数y=x2+bx+c的图象如图所示,则其对称轴方程是 ,方程x2+bx+c=0的解是 .4.下表是一组二次函数y=x2+3x-5的自变量x与函数值y的对应值:那么方程x2+3x-5=0的一个近似根是 。
【知识技能类作业】选做题:
5.已知函数y=(k-3)x2+2x+1的图象与x轴有交点,求k的取值范围.
解:当k=3时,函数y=2x+1是一次函数.∵一次函数y=2x+1与x轴有一个交点,∴k=3;当k≠3时,y=(k-3)x2+2x+1是二次函数.∵二次函数y=(k-3)x2+2x+1的图象与x轴有交点,∴Δ=b2-4ac≥0.∵b2-4ac=22-4(k-3)=-4k+16,∴-4k+16≥0.∴k≤4且k≠3.综上所述,k的取值范围是k≤4.
6.已知:抛物线y=x2+ax+a-2.(1)求证:不论a取何值时,抛物线y=x2+ax+a-2与x轴都有两个不同的交点;(2)设这个二次函数的图象与x轴相交于A(x1,0),B(x2,0),且x1、x2的平方和为3,求a的值.
(1)证明:∵Δ=a2-4(a-2)=(a-2)2+4>0,∴不论a取何值时,抛物线y=x2+ax+a-2与x轴都有两个不同的交点;(2)解:∵x1+x2=-a,x1·x2=a-2,∴x12+x22=(x1+x2)2-2x1·x2=a2-2a+4=3,∴a=1.
解:∵抛物线y=-x2+mx+3过点B(3,0), ∴0=-9+3m+3, ∴m=2.
(2)抛物线上有一点P,满足S△ABP=4S△ABD,求点P的坐标.
二次函数与一元二次方程
二次函数与一元二次方程的关系
y=ax2+bx+c(a ≠0),当y取定值时就成了一元二次方程;ax2+bx+c=0(a ≠0),右边换成y时就成了二次函数.
二次函数与一元二次方程根的情况
二次函数与x轴的交点个数
一、二次函数与一元二次方程的联系 二、二次函数图象与x轴交点问题
3.如图,直线y=mx+n与抛物线y=ax2+bx+c 交于A(-1,p),B(4,q)两点,则关于x的不 等式mx+n>ax2+bx+c的解集是______________.4.二次函数y=-x2+bx+c的图象如图,若点A(x1,y1),B(x2,y2)在此函数图象上,且x1
(2)设二次函数的图象交y轴于点C,求△ABC的面积.
数学九年级上册22.2二次函数与一元二次方程教课内容ppt课件: 这是一份数学九年级上册<a href="/sx/tb_c95442_t3/?tag_id=26" target="_blank">22.2二次函数与一元二次方程教课内容ppt课件</a>,共27页。PPT课件主要包含了h20t-5t2,h20t-5t2,观察图象完成下表,x1x23,x1-2x21,有两个交点,有两个不相等的实数根,b2-4ac0,有一个交点,有两个相等的实数根等内容,欢迎下载使用。
人教版九年级上册22.2二次函数与一元二次方程优秀课件ppt: 这是一份人教版九年级上册<a href="/sx/tb_c95442_t3/?tag_id=26" target="_blank">22.2二次函数与一元二次方程优秀课件ppt</a>,文件包含人教版数学九年级上册222《二次函数与一元二次方程》课件pptx、人教版数学九年级上册222《二次函数与一元二次方程》教案docx等2份课件配套教学资源,其中PPT共30页, 欢迎下载使用。
初中数学人教版九年级上册22.2二次函数与一元二次方程课堂教学ppt课件: 这是一份初中数学人教版九年级上册<a href="/sx/tb_c95442_t3/?tag_id=26" target="_blank">22.2二次函数与一元二次方程课堂教学ppt课件</a>,共41页。PPT课件主要包含了知识回顾,方程无实数根,方程有两个实数根,学习目标,h20t-5t2,课堂导入,二次函数,一元二次方程,知识点1,新知探究等内容,欢迎下载使用。













