河南省信阳市新县2023-2024学年七年级下学期期末数学试题（解析版）

这是一份河南省信阳市新县2023-2024学年七年级下学期期末数学试题（解析版），共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题：本题共10小题，每小题3分，共30分
1. 49的算术平方根是（ ）
A. 7B. C. D. 49
【答案】A
【解析】
【分析】本题考查了算术平方根的定义，如果，则是的平方根．若，则它有两个平方根，我们把正的平方根叫的算术平方根；若，则它的平方根是0，0的算术平方根也是0；负数没有平方根．据此求解即可．
详解】解：，
49的算术平方根是，
故选：A．
2. 秦岭是中国南北方的界山，秦岭的大散岭，凤岭，紫柏山的海拔均在1500米以上．若用米表示这些山岭的海拔，则满足的条件为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了不等式的定义．根据题意列出不等式即可求解．
【详解】解：∵山岭主峰海拔超过1500米．
∴，
故选：B．
3. 垃圾分类利国利民，某校宣传小组就“空矿泉水瓶应投放到哪种颜色的垃圾收集桶内”进行统计活动，他们随机采访50名学生并作好记录．以下是排乱的统计步骤：
①从扇形统计图中分析出本校学生对空矿泉水瓶投放的正确率
②整理采访记录并绘制空矿泉水瓶投放频数分布表
③绘制扇形统计图来表示空矿泉水瓶投放各收集桶所占的百分比
正确统计步骤的顺序应该是( )
A. ②→③→①B. ②→①→③C. ③→①→②D. ③→②→①
【答案】A
【解析】
【分析】根据统计数据收集处理的步骤即可得出结果．
【详解】解：按照统计步骤，先②整理采访记录并绘制空矿泉水瓶投放频数分布表，然后③绘制扇形统计图来表示空矿泉水瓶投放各收集桶所占的百分比，最后得出①从扇形统计图中分析出本校学生对空矿泉水瓶投放的正确率，
∴正确的步骤为：②→③→①，
故选：A．
【点睛】题目主要考查统计数据收集处理的步骤，理解题意是解题关键．
4. 4根火柴棒摆成如图所示的象形“口”字，平移火柴棒后，原图形变成的象形文字可以是（ ）

A. B. C. D.
【答案】B
【解析】
【分析】根据平移的性质，结合图形特点，采取排除法判断选项即可．
【详解】原图像水平的火柴头朝左，竖直的火柴头一根朝上一根朝下，平移后火柴头朝向不变．
A、此选项竖直火柴头均朝上，不满足平移性质，故本选项不符合题意；
B、此选项水平的火柴头朝左，竖直的火柴头一根朝上一根朝下，故本选项符合题意；
C、此选项水平的火柴头朝右，不满足平移性质，故本选项不符合题意；
D、此选项有三根火柴头朝左，不满足平移性质，故本选项不符合题意；
【点睛】本题主要考查了平移的性质，平移不改变图像的形状、大小和方向，只有位置的改变．
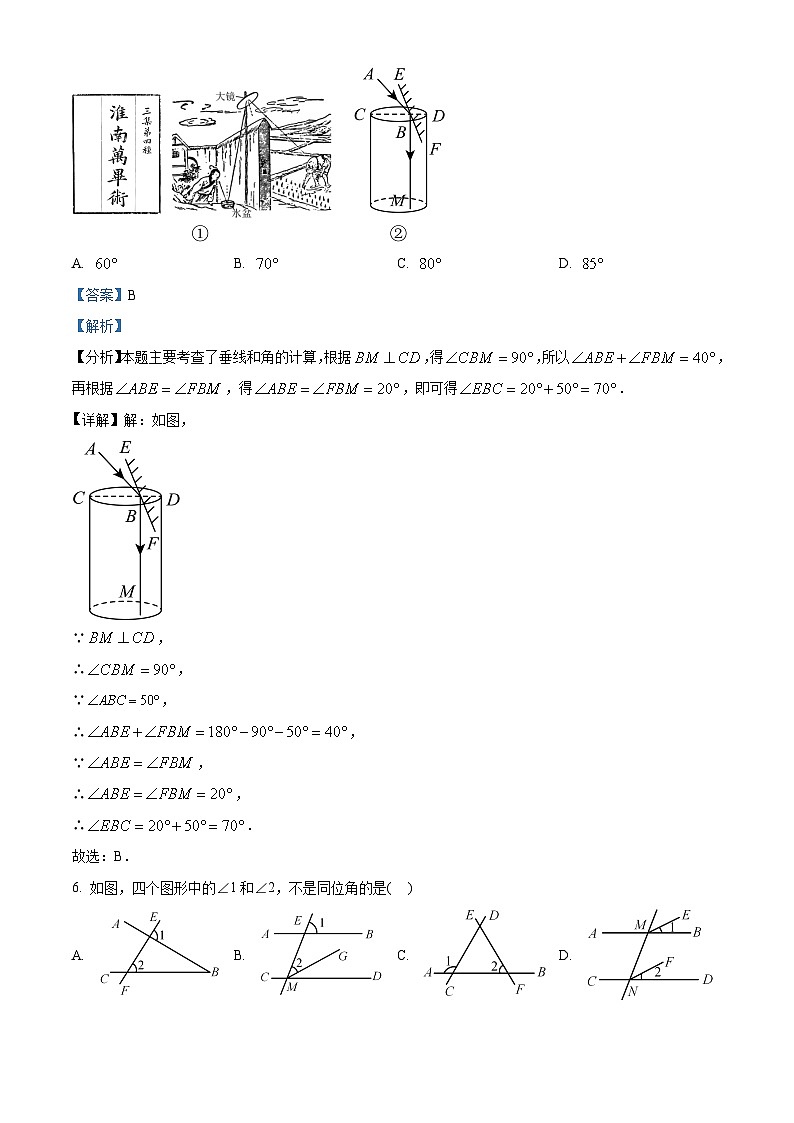
5. 如图①，汉代的《淮南万毕术》中记载的“取大镜高悬，置水盆于其下，则见四邻矣”，是古人利用光的反射定律改变光路的方法．为了探清一口深井的底部情况，如图②，在井口放置一面平面镜可改变光路，当太阳光线与地面所成夹角时，已知，要使太阳光线经反射后刚好垂直于地面射入深井底部，则需要调整平面镜与地面的夹角（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题主要考查了垂线和角的计算，根据，得，所以，再根据，得，即可得．
详解】解：如图，
∵，
∴，
∵，
∴，
∵，
∴，
∴．
故选：B．
6. 如图，四个图形中的∠1和∠2，不是同位角的是( )
A. B. C. D.
【答案】D
【解析】
【分析】要想成为同位角，两个角必须有一对边在同一条直线上，依据这一条件分析判断即可．
【详解】A、∠1、∠2有一条边在一条直线上，另一条边在被截线的同一方，是同位角；
C、∠1、∠2有一条边在一条直线上，另一条边在被截线的同一方，是同位角；
D、∠1、∠2有一条边在一条直线上，另一条边在被截线的同一方，是同位角；
D、∠1、∠2的两条边都不在一条直线上，不是同位角；
故选：D
【点睛】本题考查同位角定义，解题的关键是熟悉三线八角的位置关系．
7. 周末，洋洋参加了褐马鸡放归活动．如图是宣传牌上利用网格画出的褐马鸡的示意图．若建立适当的平面直角坐标系，表示嘴部点的坐标为，表示尾部点的坐标为，则表示足部点的坐标为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题主要考查了用坐标确定位置，依据已知点的坐标确定出坐标轴的位置是解题的关键．根据A点的坐标为，B点的坐标为确定出坐标轴的位置，即可求得C点的坐标．
【详解】解：由表示嘴部A点的坐标为，表示尾部B点的坐标为，得出坐标系如图所示：
∴表示足部C点的坐标为．
故选：C．
8. 为了调查疫情对青少年人生观、价值观产生的影响，某学校团委对初二级部学生进行了问卷调查，其中一项是：疫情期间出现的哪一个高频词汇最触动你的内心？针对该项调查结果制作的两个统计图（不完整）如下，由图中信息可知，下列结论错误的是（ ）
A. 本次调查的样本容量是
B. 选“责任”的有人
C. 扇形统计图中“生命”所对应的扇形圆心角度数为
D. 选“感恩”的人数最多
【答案】C
【解析】
【分析】根据条形统计图与扇形统计图中的相关数据进行计算并逐一判断即可得解．
【详解】A.由统计图可知“奉献”对应的人数是108人，所占比为18%，则调查的样本容量是，故A选项正确；
B.根据扇形统计图可知“责任”所对的圆心角是，则所对人数为人，故B选项正确；
C.根据条形统计图可知“生命”所对的人数为132人，则所对的圆心角是，故C选项错误；
D.根据“敬畏”占比为16%，则对应人数为人，则“感恩”的人数为人，人数最多，故D选项正确，
故选：C．
【点睛】本题主要考查了通过条形统计图与扇形统计图之间各部分数量与占比的关系对总体，未知部分对应数量以及对应圆心角的求解，数量掌握相关计算方法是解决本题的关键．
9. 某爱心组织开展图书捐赠活动，以教育助力乡村振兴，下表是本次购买图书的发票，部分数据看不清，根据其他数据求出购买爱的教育、边城的数量分别为（ ）
A. 15，10B. 10，15C. 12，13D. 13，12
【答案】A
【解析】
【分析】本题主要考查了二元一次方程组的应用，设购买爱的教育x本，边城y本，根据题意列出关于x，y的二元一次方程组求解即可得出答案．
【详解】解：设购买爱的教育x本，边城y本，
根据题意有：，
解得：，
则购买爱的教育15本，边城10本，
故选：A．
10. 数学中有许多优美、寓意美好的曲线．在平面直角坐标系中，绘制如图所示的曲线，给出下列四个结论：①曲线经过的整点即横、纵坐标均为整数的点中，横纵坐标互为相反数的点有2个；②曲线在第一、二象限中的任意一点到原点的距离都大于1；③曲线所围成的“心形”区域的面积大于3，其中正确的有（ ）
A. ①②B. ①②③C. ①③D. ②③
【答案】D
【解析】
【分析】本题考查了坐标系中图形的面积，图形的对称性，点与象限的关系，点与圆的关系，熟练掌握图形的对称性，点与象限的关系，点与圆的关系，是解题的关键．根据曲线的对称性，正方形的性质，面积求法，结合坐标系可以判定．
【详解】解：如图，连接，，
∵曲线经过点0,1，，1,0，，，-1,1，
∴①错误；
∵曲线在第一、二象限中的任意一点都在以O为圆心，以1为半径的圆外，
∴曲线在第一、二象限中的任意一点到原点的距离大于1，
∴②正确；
∵的面积为，
∵四边形是长方形且，，
∴长方形面积为2，
∴长方形面积与的面积和为3，
∵曲线所围成的“心形”区域的面积大于矩形的面积与的面积和，
∴曲线所围成的“心形”区域的面积大于3，
∴③正确；
故选∶D．
二、填空题：本题共5小题，每小题3分，共15分
11. 比较大小：_______（填“>”、“
【解析】
【详解】∵40，
∴.
故答案为：>.
12. 端午节期间，食品药品监督局对市场上的粽子质量进行了调查，你认为适合采用的调查方式是______调查．（填“全面”或“抽样”）
【答案】抽样
【解析】
【分析】普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．
【详解】解：因为市场上的粽子数量很大，不适合普查，所以选择抽样调查．
故答案为：抽样．
【点睛】本题考查抽样调查，解题的关键是掌握抽样调查的特点和定义．
13. 已知关于，的二元一次方程组的解，则的算术平方根是_____.
【答案】2
【解析】
【详解】分析：把代入方程组，得出关于a、b的方程组，求出方程组的解即可．
详解：把代入方程组得：，
解得：，
所以2a-4b=，
∴的算术平方根是2,
故答案为:2．
点睛：本题考查了解二元一次方程组和二元一次方程组的解，能得出关于a、b的方程组是解此题的关键．
14. 已知是关于x的一元一次不等式，则m的值为______．
【答案】m=2
【解析】
【分析】根据一元一次不等式的定义，|m-3|=1，m-4≠0，分别进行求解即可．
【详解】解：根据题意|m-3|=1，m-4≠0，
所以m-3=±1，m≠4，
解得m=2．
故答案为：m=2．
【点睛】本题考查了一元一次不等式的定义和绝对值．解题的关键是明确一元一次不等式的定义中的未知数的最高次数为1次，还要注意未知数的系数不能是0．
15. 如图，第四象限内有一正方形，且，，将正方形平移，使A，C两点分别落在两条坐标轴上，则平移后点C的坐标是________
【答案】或
【解析】
【分析】本题主要考查图形的平移及平移特征，图形的平移与图形上某点的平移规律相同，解题的关键是掌握平移中点的变化规律：横坐标右移加，左移减，纵坐标上移加，下移减．根据题意，分两种情况讨论：当平移后点的对应点在轴上，点的对应点在轴上时；当平移后点的对应点在轴上，点的对应点在轴上时；分别根据轴、轴上点的坐标特征解答即可．
【详解】解：根据题意，分两种情况讨论如下：
当平移后点的对应点在轴上，点的对应点在轴上时，则平移后点的纵坐标为0，点的横坐标为0，
在第四象限正方形中，，，
，
由点的纵坐标由到平移后为0，可知向上平移了个单位；由点的横坐标由到平移后为0，可知向左平移了个单位，
平移后点的对应点的纵坐标是，
平移后点的对应点的坐标是；
当平移后点的对应点在轴上，点的对应点在轴上时，则平移后点的横坐标为0，点的纵坐标为0，
在第四象限正方形中，，，
，
由点的横坐标可知向左平移了个单位，由点的纵坐标可知向上平移了个单位，
平移后点的对应点的横坐标是，
平移后点的对应点的坐标是；
综上所示，平移后点的对应点的坐标是或，
故答案为：或．
三、解答题：本题共8小题，共75分
16. 解下列方程组：
（1）
（2）
【答案】（1）
（2）
【解析】
【分析】本题考查解二元一次方程组：
（1）加减法解方程即可；
（2）加减法解方程即可．
【小问1详解】
解：，
，得：，解得：，
把代入①，得：，解得：，
∴方程组的解为：；
【小问2详解】
，
，得：，解得：，
把代入①，得：，解得：，
∴方程组的解为：．
17. 解不等式组，并将解集在数轴上表示出来：．
【答案】无解，在数轴上表示见解析
【解析】
【分析】本题考查了解一元一次不等式组，在数轴上表示不等式组的解集．按照解一元一次不等式组的步骤，进行计算即可解答．
【详解】解：，
解不等式①得：，
解不等式②得：，
原不等式组无解，
该不等式组的解集在数轴上表示如图所示：
．
18. 已知a是2的平方根，b是（﹣13）2的平方根，c的立方根是﹣3，d的算术平方根是，回答下列问题．
（1）分别求出a，b，c，d的值；
（2）d的另外一个平方根落在图中的 ．（填“段①”“段②”“段③”“段④”）
【答案】（1）a=±，b=±13；c=-27，d=2
（2）段②
【解析】
【分析】（1）根据平方根和立方根的知识可求得此题结果；
（2）先求得d的另外一个平方根为，再比较出它在数轴中所在的位置．
【小问1详解】
解：（1）∵（±）2==，（±13）2=（13）2，（3）3=27，（）2=2，
∴±是平方根，±13是（13）2的平方根，27的立方根是3，2的算术平方根是，
∴，b=±13，c=27，d=2；
【小问2详解】
解：∵2的平方根是±，
而，
∴d的另外一个平方根落在图中的“段②”，
故答案为：“段②”．
【点睛】此题考查了运用平方根和立方根解决问题的能力，关键是能准确理解并运用以上知识．
19. 为了解本校八年级学生的暑期课外阅读情况，某数学兴趣小组抽取了50名学生进行问卷调查．
（1）下面的抽取方法中，应该选择（ ）
A.从八年级随机抽取一个班的50名学生
B.从八年级女生中随机抽取50名学生
C.从八年级所有学生中随机抽取50名学生
（2）对调查数据进行整理，得到下列两幅尚不完整的统计图表：
暑期课外阅读情况统计表

统计表中的__________，补全条形统计图；
（3）若八年级共有800名学生，估计八年级学生暑期课外阅读数量达到2本及以上的学生人数；
（4）根据上述调查情况，写一条你的看法．
【答案】（1）C （2）15；见解析
（3）八年级学生暑期课外阅读数量达到2本及以上的学生约为320人；
（4）答案不唯一，见解析
【解析】
【分析】本题考查了抽样调查的可靠性，频数分布表以及条形统计图，熟练掌握条形统计图是解题的关键．
（1）根据所抽取的样本必须具有广泛性和代表性，即可解答；
（2）用样本容量减去总计量为0本，1本以及3本及以上的人数可得a的值，再补全条形统计图即可；
（3）用800乘以样本中暑期课外阅读数量达到2本及以上所占百分比即可得出结论；
（4）根据统计表的数据提出建议即可．
【小问1详解】
解：为了解本校八年级学生的暑期课外阅读情况，应该选择从八年级所有学生中随机抽取50名学生，这样抽取的样本具有广泛性和代表性，
故选：C；
【小问2详解】
解：；
故答案为：15；
补全条形统计图如图所示：
；
【小问3详解】
解：（人）
答：八年级学生暑期课外阅读数量达到2本及以上的学生约为320人；
【小问4详解】
解：本次调查大部分同学一周暑期课外阅读数量达不到3本，建议同学们多阅读，培养热爱读书的良好习惯（答案不唯一）．
20. 如图，将向左、向下分别平移5个单位，得到．

（1）画出；
（2）求出的面积；
（3）若点是内一点，直接写出点P平移后对应点的坐标．
【答案】（1）见解析 （2）2.5
（3）
【解析】
【分析】本题考查了平移作图，坐标与图形，点坐标的平移．熟练掌握平移的性质作图是解题的关键．
（1）根据平移的性质作图即可；
（2）根据，计算求解即可；
（3）根据点坐标平移，左减右加，上加下减，求解作答即可．
【小问1详解】
解：如图，即为所求；
【小问2详解】
解：由题意知，，
∴的面积为；
【小问3详解】
解：由题意知，点平移后对应点的坐标为 ．
21. 某大型企业为了保护环境，准备购A、B两种型号的污水处理设备共10台，一台A型设备的单价为12万，一台B型设备的单价为10万元，经了解，一台A型设备每月可处理污水220吨，一台B型设备每月可处理污水190吨，如果该企业计划用不超过106万元的资金购买这两种设备，而且使这两种设备每月的污水处理量不低于2005吨，请通过计算说明这种方案是否可行．
【答案】该企业计划投入不超过106万购买这两种设备不可行．
【解析】
【分析】本题考查的是不等式组的实际应用．设购买型污水处理设备台，根据题意可以列出相应的不等式组，从而可以解答本题．
【详解】解：该企业投入106万购买这两种设备不可行，
理由：设购买型污水处理设备台，
，
解得且，
该不等式组无解，
∴该企业计划投入不超过106万购买这两种设备不可行．
22. 为了抓住文化艺术节的商机，某商店决定购进A，B两种艺术节纪念品．若购买8件A种纪念品和3件B种纪念品，则需要950元；若购买5件A种纪念品和6件B种纪念品，则需要800元．
（1）求购进A，B两种纪念品每件各需多少元？
（2）若该商店购买A种纪念品的数量比B种纪念品的数量的2倍少10件，且购买B种纪念品不少于33件，考虑市场需求和资金周转，用于购买纪念品的资金不超过8000元．求该商店共有几种进货方案？
【答案】（1）A种纪念品每件100元，B种纪念品每件50元
（2）有四种方案
【解析】
【分析】本题考查二元一次方程组的实际应用，一元一次不等式的实际应用．解题的关键是正确的列出方程和不等式．
（1）设A种纪念品每件需x元，B种纪念品每件需y元，根据题意，列出方程组进行求解即可；
（2）设商店可购进B纪念品a件，根据题意列出一元一次不等式进行求解即可．
【小问1详解】
解：设A种纪念品每件需x元，B种纪念品每件需y元，由题意，得：
，
解得：．
答：A种纪念品每件100元，B种纪念品每件50元；
【小问2详解】
解：设商店可购进B纪念品a件，则购进A纪念品件，
由题意得，
解得：．
∵购买B种纪念品不少于33件，
∴．
有四种方案：可购进A种纪念品56件，B种纪念品33件；
可购进A种纪念品58件，B种纪念品34件；
可购进A种纪念品60件，B种纪念品35件；
可购进A种纪念品62件，B种纪念品36件．
23. 已知∶点A、C、B不同一条直线上，AD∥BE．
（1）如图①，当∠A=58°，∠B=118°时，求∠C的度数；
（2）如图②，AQ、BQ分别为∠DAC、∠EBC的平分线所在直线，试探究∠C与∠AQB的数量关系；
（3）如图③，在（2）的前提下，且有AC∥QB，QP⊥PB，直接写出∠DAC∶∠ACB∶∠CBE的值．
【答案】（1）120°；（2）2∠AQB+∠C=180°；（3）1：2：2
【解析】
【分析】（1）过点C作CF∥AD，则CF∥BE，根据平行线的性质可得出∠ACF=∠A、∠BCF=180°-∠B，将其代入∠ACB=∠ACF+∠BCF即可求出∠ACB的度数；
（2）过点Q作QM∥AD，则QM∥BE，根据平行线的性质、角平分线的定义可得出∠AQB=（∠CBE-∠CAD），结合（1）的结论可得出2∠AQB+∠C=180°；
（3）由（2）的结论可得出∠CAD=∠CBE①，由QP⊥PB可得出∠CAD+∠CBE=180°②，联立①②可求出∠CAD、∠CBE的度数，再结合（1）的结论可得出∠ACB的度数，将其代入∠DAC：∠ACB：∠CBE中可求出结论．
【详解】解：（1）在图①中，过点C作CF∥AD，则CF∥BE．
∵CF∥AD∥BE，
∴∠ACF=∠A，∠BCF=180°-∠B，
∴∠ACB=∠ACF+∠BCF=180°-（∠B-∠A）=120°．
（2）在图②中，过点Q作QM∥AD，则QM∥BE．
∵QM∥AD，QM∥BE，
∴∠AQM=∠NAD，∠BQM=∠EBQ．
∵AQ平分∠CAD，BQ平分∠CBE，
∴∠NAD=∠CAD，∠EBQ=∠CBE，
∴∠AQB=∠BQM-∠AQM=（∠CBE-∠CAD）．
∵由（1）可得∠C=180°-（∠CBE-∠CAD）=180°-2∠AQB，
∴2∠AQB+∠C=180°．
（3）∵AC∥QB，
∴∠AQB=∠CAP=∠CAD，∠ACP=∠PBQ=∠CBE，
∴∠ACB=180°-∠ACP=180°-∠CBE．
∵2∠AQB+∠ACB=180°，
∴∠CAD=∠CBE．
又∵QP⊥PB，
∴∠CAP+∠ACP=90°，即∠CAD+∠CBE=180°，
∴∠CAD=60°，∠CBE=120°，
∴∠ACB=180°-（∠CBE-∠CAD）=120°，
∴∠DAC：∠ACB：∠CBE=60°：120°：120°=1：2：2．
【点睛】本题考查了平行线的性质、邻补角、角平分线以及垂线，解题的关键是：（1）根据平行线的性质结合角的计算找出∠ACB=180°-（∠B-∠A）；（2）根据平行线的性质、角平分线的定义找出∠AQB=（∠CBE-∠CAD）；（3）由AC∥QB、QP⊥PB结合（1）（2）的结论分别求出∠DAC、∠ACB、∠CBE的度数．阅读数量（本）
人数
0
5
1
25
2
3本及以上
5
合计
50