浙教版（2024）八年级上册2.3 等腰三角形的性质定理教学演示课件ppt

这是一份浙教版（2024）八年级上册2.3 等腰三角形的性质定理教学演示课件ppt，共24页。PPT课件主要包含了学习目标，回顾旧知，°30°，°35°，即时演练，求证BDCE，BDCE，△BCE≌△CBD，∠BCE∠CBD，∠ABC∠ACB等内容，欢迎下载使用。

1.了解等腰三角形的有关概念；   2.掌握等腰三角形的性质定理； 3.能运用等腰三角形的性质定理进行简单的计算和证明
有两条边相等的三角形叫做等腰三角形.
等腰三角形的对称轴是：
顶角平分线所在的直线是它的对称轴
三条边都相等的三角形叫做等边三角形.
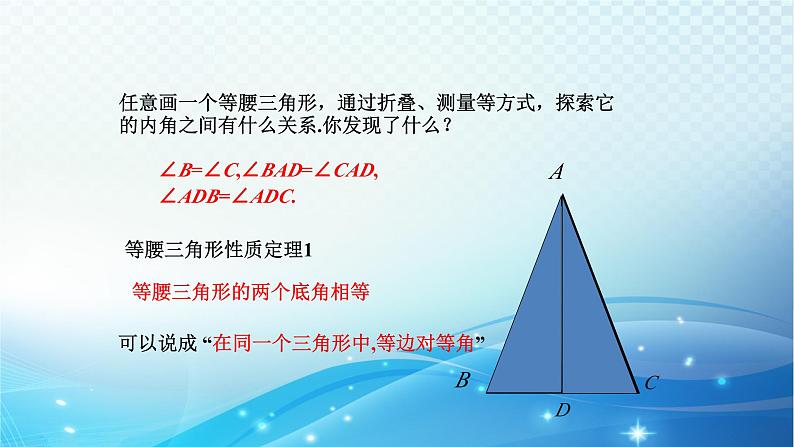
任意画一个等腰三角形，通过折叠、测量等方式，探索它的内角之间有什么关系.你发现了什么？
∠B=∠C,∠BAD=∠CAD,∠ADB=∠ADC.
可以说成 “在同一个三角形中,等边对等角”
等腰三角形的两个底角相等
等腰三角形性质定理1
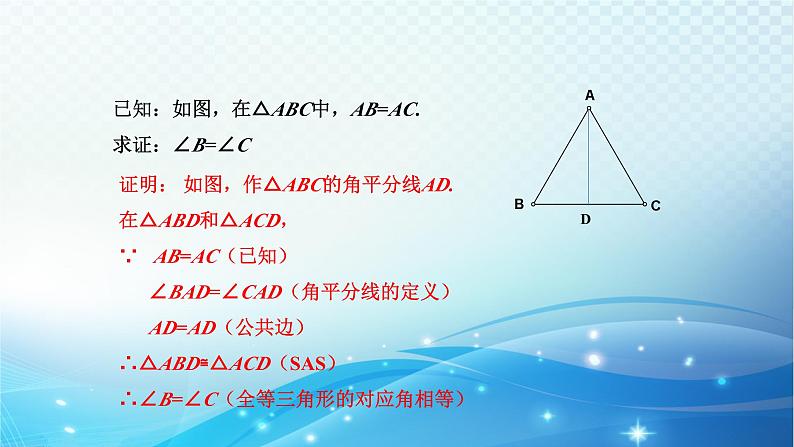
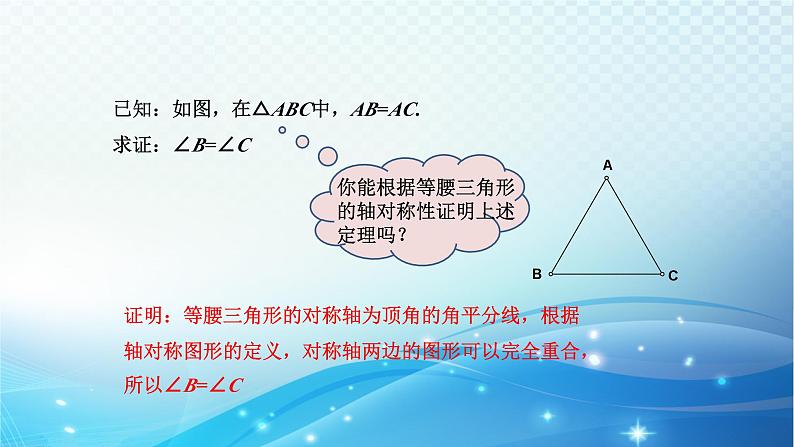
已知：如图，在△ABC中，AB=AC.求证：∠B=∠C
证明： 如图，作△ABC的角平分线AD.在△ABD和△ACD，∵ AB=AC（已知） ∠BAD=∠CAD（角平分线的定义） AD=AD（公共边）∴△ABD≌△ACD（SAS）∴∠B=∠C（全等三角形的对应角相等）
证明：等腰三角形的对称轴为顶角的角平分线，根据轴对称图形的定义，对称轴两边的图形可以完全重合，所以∠B=∠C
⒈等腰三角形一个底角为75°,它的另外两个角为__________ ⒉等腰三角形一个角为70°,它的另外两个角为 ___________________ ⒊等腰三角形一个角为110°,它的另外两个角为__________
结论:在等腰三角形中,① 顶角+2×底角=180°② 顶角=180°－2×底角
④0°＜顶角＜180°⑤0°＜底角＜90°
70°,40°或55°,55°
③ 底角=（180°－顶角）÷2
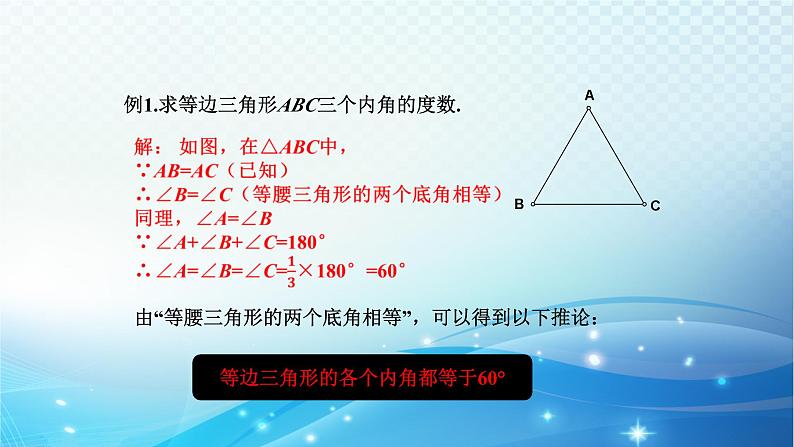
例1.求等边三角形ABC三个内角的度数.
由“等腰三角形的两个底角相等”，可以得到以下推论：
等边三角形的各个内角都等于60°
如图，等边△ABC中，D为AC的中点，E是BC延长线上一点，且CE=CD，求证：DB=DE.
例2：求证：等腰三角形两底角的平分线相等.
已知：如图，在△ABC中，AB=AC，BD，CE是△ABC的两条角平分线.
BD,CE是△ABC的角平分线
已知：如图，在△ABC中，BP、CP分别平分∠ABC和∠ACB，DE过点P交AB于D，交AC于E，且DE∥BC．求证：DE﹣DB=EC．
证明：∵BP平分∠ABC， ∴∠DBP=∠CBP． ∴DE∥BC， ∴∠CBP=∠DPB． ∴∠DPB=∠DBP．即DP=DB． 同理可得PE=CE． ∴DE=BD+CE，即DE﹣DB=EC．
1.如图，△ABC中，∠ABC=2∠C，BE平分∠ABC交AC于E，AD⊥BE于D，下列结论： ①AC-BE=AE；②∠BAD-∠C=∠DAE；③∠DAE=∠C；④AC=2BD，其中正确的是（　　） A．①②③ B．①③④ C．①②④ D．②③④
【解析】∵BE平分∠ABC， ∴∠1=∠2， ∵∠ABC=2∠C， ∴∠2=∠C， ∴BE=CE， ∵AC-CE=AE， ∴AC-BE=AE，故①正确；
延长AD交BC与F， ∵AD⊥BE， ∴∠ADB=∠FDB=90°， ∵在△ABD和△FBD中， ∠ADB=∠FDB=90°BD=BD∠1=∠2 ∴△ABD≌△FBD（ASA）， ∴∠BAD=∠AFB， 在△ACF中，∠DAE=∠AFB-∠C， ∴∠BAD-∠C=∠DAE，故②正确；
在Rt△ABD中，∠BAD=90°-∠1=90°-∠C， ∴90°-∠C-∠C=∠DAE， ∴∠DAE=90°-2∠C，故③错误；
取CF的中点G，连接DG，则DG是△ACF的中位线， ∴DG∥AC，AC=2DG， ∴∠C=∠3， ∴∠2=∠3， ∴BD=DG， ∴AC=2BD，故④正确； 综上所述，正确的结论有①②④． 故选C．
2.已知：如图，AB=AC，DB=DC，问：AD与BC有什么关系？
猜想：AD垂直平分BC
证明: ∵AB=AC,BD=CD,AD=DA
∴△ABD≌△ACD(SSS)
3.如图，在△ABC中，∠ACB=90°，AD=AC，BE=BC，则∠DCE的大小为（　　）A．30° B．45° C．60° D．无法确定
【解析】设∠ACE=x度，∠ECD=y度，∠DCB=z度， ∵BC=BE， ∴∠CED=∠ECB=（y+z）度， 又AC=AD， ∠ADC=∠ACD=（x+y）度， 在△CDB中，∠B=x+y-z； 在△ACE中，∠A=y+z-x； 在△ABC中，∠ACB=90°， ∴∠A+∠B=90°，即x+y-z+y+z-x=90°， ∴2y=90°，解得y=45度．于是∠DCE=45°．
4.如图，等边△ABC的三条角平分线相交于点O，OD∥AB交BC于D，OE∥AC交BC于点E，那么这个图形中的等腰三角形共有（　　） A．5个 B．6个 C．7个 D．8个
①∵△ABC为等边三角形， ∴AB=AC， ∴△ABC为等腰三角形； ②∵BO，CO，AO分别是三个角的角平分线， ∴∠ABO=∠CBO=∠BAO=∠CAO=∠ACO=∠BCO， ∴AO=BO，AO=CO，BO=CO， ∴△AOB为等腰三角形； ③△AOC为等腰三角形； ④△BOC为等腰三角形； ⑤∵OD∥AB，OE∥AC， ∴∠B=∠ODE，∠C=∠OED， ∵∠B=∠C， ∴∠ODE=∠OED， ∴△DOE为等腰三角形；
⑥∵OD∥AB，OE∥AC， ∴∠BOD=∠ABO，∠COE=∠ACO， ∵∠DBO=∠ABO，∠ECO=∠ACO， ∴∠BOD=∠DBO，∠COE=∠ECO， ∴△BOD为等腰三角形； ⑦△COE为等腰三角形．
5.在△ABC中，AD平分∠BAC，E是BC上一点，BE=CD，EF∥AD交AB于F点，交CA的延长线于P，CH∥AB交AD的延长线于点H， ①求证：△APF是等腰三角形；      ②猜想AB与PC的大小有什么关系？证明你的猜想．
①证明：∵EF∥AD， ∴∠1=∠4，∠2=∠P， ∵AD平分∠BAC， ∴∠1=∠2， ∴∠4=∠P， ∴AF=AP， 即△APF是等腰三角形；
②AB=PC．理由如下： 证明：∵CH∥AB， ∴∠5=∠B，∠H=∠1， ∵EF∥AD， ∴∠1=∠3， ∴∠H=∠3， 在△BEF和△CDH中， ∵∠5=∠B∠H=∠3BE=CD，∴△BEF≌△CDH（AAS），∴BF=CH，∵AD平分∠BAC，∴∠1=∠2，∴∠2=∠H，∴AC=CH，∴AC=BF，∵AB=AF+BF，PC=AP+AC，∴AB=PC．
在等边△ABC所在的平面内求一点P，使△PAB，△PBC，△PAC都是等腰三角形，具有这样性质的点P有（　　）个A．1B．4C．7D．10
【解析】（1）点P在三角形内部时，点P是边AB、BC、CA的垂直平分线的交点，是三角形的外心； （2）分别以三角形各顶点为圆心，边长为半径，交垂直平分线的交点就是满足要求的．每条垂直平分线上得3个交点，再加三角形的垂心，一共10个．故具有这种性质的点P共有10个． 故选D．