





初中数学浙教版(2024)八年级上册2.5 逆命题和逆定理评课课件ppt
展开了解逆命题、逆定理的概念.会识别两个命题是不是互逆命题,并能写出简单命题的逆命题.了解原命题成立,其逆命题不一定成立.理解线段垂直平分线性质定理的逆定理.
考虑两个命题:“飞机是会飞的交通工具”“会飞的交通工具是飞机”这两个命题有什么不同?它们都是真命题吗?
1. 命题的概念:一般地,判断某一件事情的句子叫做命题.2.命题一般由_____和_____两部分组成,即它的一般形式是___________________. 3.下列句子是命题的是( ) A. 画∠AOB=45° B. 小于直角的角是锐角吗? C. 连结CD D. 鸟是动物
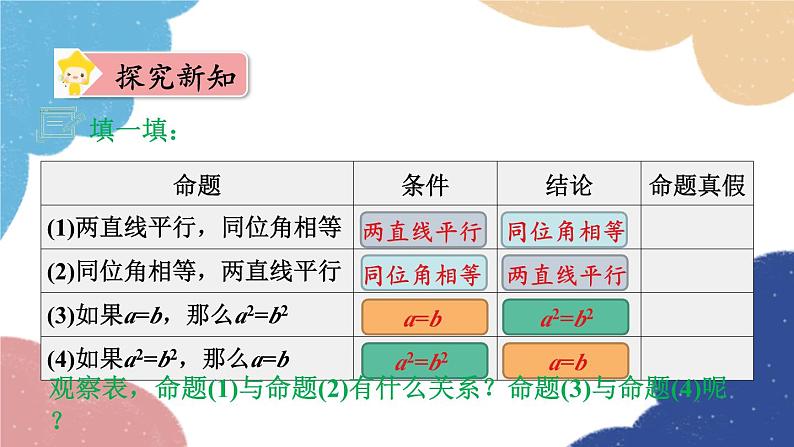
观察表,命题(1)与命题(2)有什么关系?命题(3)与命题(4)呢?
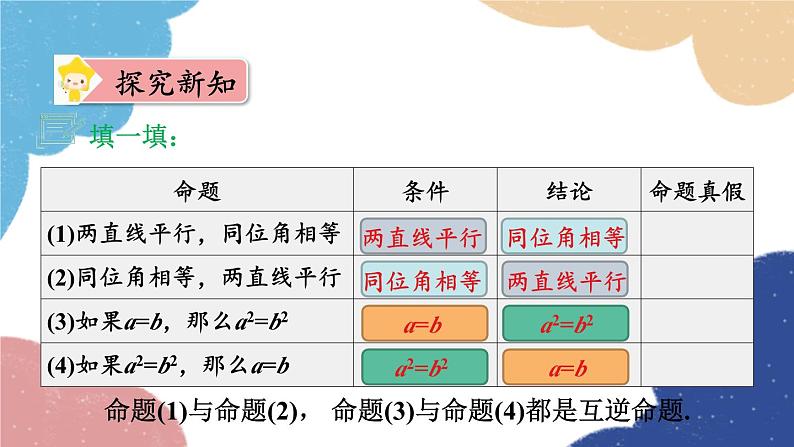
互逆命题在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.原命题与逆命题如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题.
命题(1)与命题(2), 命题(3)与命题(4)都是互逆命题.
原命题是真命题,它的逆命题不一定是真命题.
做一做:说出下列命题的逆命题,并判定命题的真假:(1) 两直线平行,内错角相等.(3) 磁悬浮列车是一种高速行驶时不接触地面的交通工具.
内错角相等,两直线平行.
高速行驶时不接触地面的交通工具是磁悬浮列车.
每个命题都有它的逆命题,但每个真命题的逆命题不一定是真命题,同样,每个假命题的逆命题也不一定是假命题.写出一个命题的逆命题的关键是分清它的条件和结论,然后将条件和结论互换.
想一想:你能根据已经学过的定理和逆命题的定义类比出逆定理的定义吗?
(一个命题经证明是真命题,就可称为定理. )
原定理和逆定理如果一个定理的逆命题能被证明是真命题,那么就叫它是原定理的逆定理,这两个定理叫做互逆定理.
解:这个定理的逆命题是: 到线段两端距离相等的点在线段的垂直平分线上.下面给出证明.已知:如图,AB是一条线段,P是一点,且PA=PB.求证:点P在线段AB的垂直平分线上.
已知:如图,AB是一条线段,P是一点,且PA=PB.求证:点P在线段AB的垂直平分线上.
分析:要证明点P在线段AB的垂直平分线上,可以过点P作AB的垂线,然后证明它恰好平分线段AB.
证明:(1)当点P在线段AB上,结论显然成立;(2)当点P不在线段AB上时,作PO⊥AB于点O.∵PA=PB,PO⊥AB, ∴OA=OB(等腰三角形三线合一).∴PO是AB的垂直平分线.∴点P在线段AB的垂直平分线上.
线段垂直平分线性质定理的逆定理 ①文字语言: 到线段两端距离相等的点在线段的垂直平分线上. ②几何语言:∵PA =PB,∴点P 在AB 的垂直平分线上.
例1 说出下列命题的逆命题,并判定是真命题还是假命题:(1)同位角相等;(2)长方形有两条对称轴.
解: (1)的逆命题为:相等的两个角为同位角,是假命题.(2)的逆命题为:有两条对称轴的图形为长方形,是假命题.
例2 下列定理中哪些有逆定理?如果有逆定理,说出它的逆定理.(1)同旁内角互补,两直线平行;(2)对顶角相等;(3)三角形的两边之和大于第三边.
解: (2) (3)没有逆定理, (1) 有逆定理.(1)的逆定理为:两直线平行,同旁内角互补.
例3 说出命题“两个全等三角形的面积相等”的逆命题,判断这个命题的真假,并给出证明.
解: 逆命题是 “如果两个三角形的面积相等,那么这两个三角形全等”.分析:说明一个命题是真命题需经过证明,而说明一个命题是假命题只需举一个反例即可.
解: 逆命题是 “如果两个三角形的面积相等,那么这两个三角形全等”.如图,在△ABC和△ABE中,CD、EF分别是△ABC和△ABE的AB边上的高线,且CD=EF,则△ABC和△ABE的面积相等,但显然它们不全等.所以这个逆命题是假命题.
这个命题是假命题. 举反例如下:
1. 判断下列说法是否正确?如果不正确,请说明理由.(1) 每个定理都有逆定理;(2) 每个命题都有逆命题;(3) 互逆命题同真同假;(4) 对顶角相等没有逆定理.
每个定理不一定有逆定理,只有定理的逆命题是真命题时才称它为原定理的逆定理.
每个真命题的逆命题不一定是真命题,每个假命题的逆命题也不一定是假命题.
2. 写出下列各命题的逆命题,并判断逆命题的真假:(1) 如果|a|=|b|,那么a=b;(2) 等边三角形的三个角都是60°;(3) 互为相反数的两个数的和为0.
逆命题:如果a=b,那么|a|=|b|. 真命题
逆命题:三个角都是60°的三角形是等边三角形.真命题
逆命题:如果两数和为0,那么这两个数互为相反数. 假命题
3. 判断下面两个定理是否有逆定理,若有,请写出它的逆定理,若没有,说明理由.(1)在一个三角形中,等角对等边;(2)四边形的内角和等于360°.
解:(1)有逆定理,逆定理为:在一个三角形中,等边对等角.(2)有逆定理,逆定理为:内角和等于360°的多边形是四边形.
3. 求证:三角形三条边的垂直平分线相交于一点.
已知:在△ABC中,PD,PE分别是AB,AC的垂直平分线,相交于点P.求证:点P也在BC的垂直平分线上.
证明:连结PA,PB,PC.∵ PD,PE分别是AB,AC的垂直平分线,∴ PA=PB,PA=PC(线段垂直平分线 上的点到线段 两端的距离相等) . ∴ PB=PC(等量代换), ∴点P在BC的垂直平分线上(到线段两端距离相等的点在线段的垂直平分线上).
① 逆命题、逆定理的概念;② 能写出一个命题的逆命题;③ 在证明假命题时会用举反例说明;④ 线段垂直平分线性质定理的逆定理.
浙教版八年级上册2.5 逆命题和逆定理授课课件ppt: 这是一份浙教版八年级上册2.5 逆命题和逆定理授课课件ppt,共15页。PPT课件主要包含了什么是命题,同位角相等,两直线平行,探索新知,做一做,按要求作答,几何语言等内容,欢迎下载使用。
2020-2021学年2.5 逆命题和逆定理课文内容课件ppt: 这是一份2020-2021学年2.5 逆命题和逆定理课文内容课件ppt,共17页。PPT课件主要包含了问题1什么是命题,知识回顾,探索新知,真命题,3对顶角相等,有逆定理,没有逆定理,几何语言,两者是互逆定理等内容,欢迎下载使用。
初中数学浙教版八年级上册2.5 逆命题和逆定理集体备课课件ppt: 这是一份初中数学浙教版八年级上册2.5 逆命题和逆定理集体备课课件ppt,共16页。PPT课件主要包含了知识回顾,互逆命题,2同位角相等,相等的角是同位角,真命题,假命题,没有逆定理,试一试,几何语言,新知应用等内容,欢迎下载使用。













