

2024—2025学年上学期北京初中数学八年级开学模拟试卷1(含答案)
展开
这是一份2024—2025学年上学期北京初中数学八年级开学模拟试卷1(含答案),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1.如图所示,在四边纸片ABCD中,AD//BC,AB//CD,将纸片沿EF折叠,点A,D分别落在Aˈ,Dˈ处,且AˈDˈ经过点B,FDˈ交BC于点G,连接EG,若EG平分∠FEB,EG//AˈDˈ,∠DˈFC=80°,则∠A的度数是( )
A. 65°B. 70°C. 75°D. 80°
2.用三根木条首尾顺次连接形成三角形框架,其中两根木条长分别为2cm,4cm,则第三根木条长可以是( )
A. 2cmB. 4cmC. 6cmD. 8cm
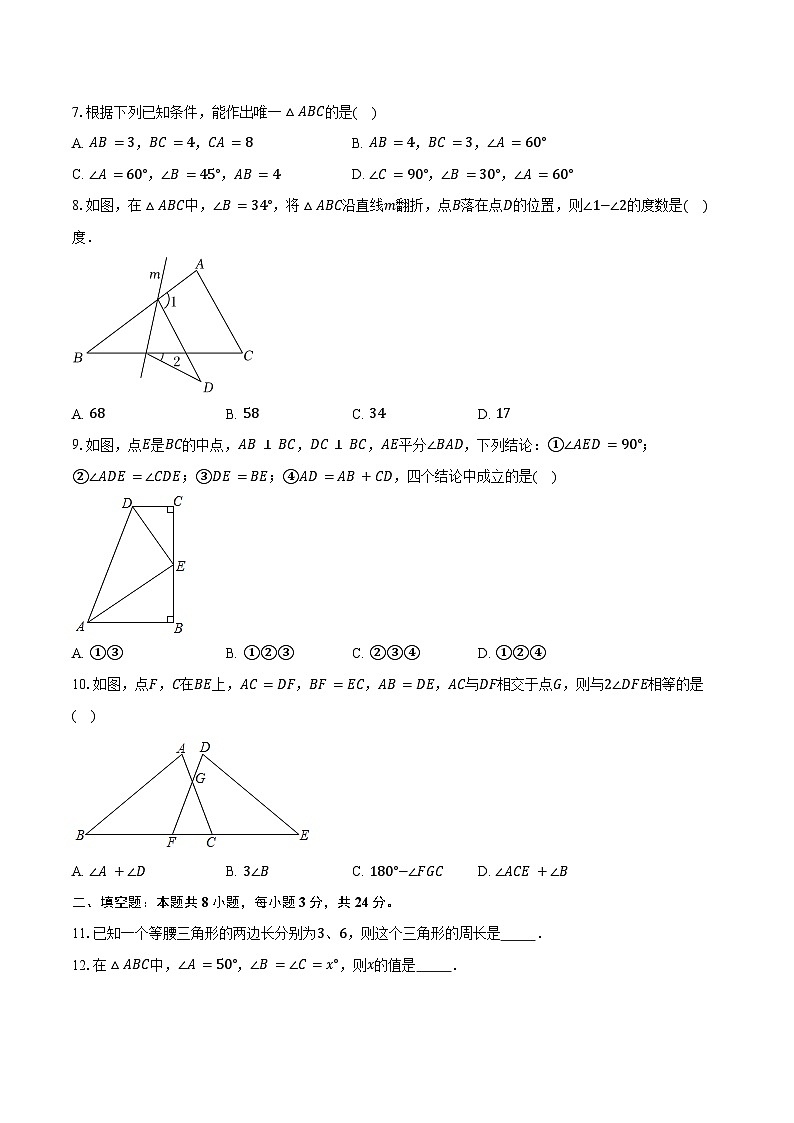
3.如图,三角形的一边BC在直线n上,直线m//n,∠1=55°,∠CBA=60°,则∠A=( )
A. 65°B. 75°C. 55°D. 60°
4.若正多边形的内角和是1260°,则该正多边形的一个外角为( )
A. 30°B. 40°C. 45°D. 60°
5.如图,△ABC≌△DEF,BC=7,EC=4,则CF的长为( )
A. 2B. 3
C. 5D. 7
6.如图,点P在∠ABC的平分线上,PD⊥BC于点D,若PD=4,则P到BA的距离为( )
A. 3B. 4C. 5D. 6
7.根据下列已知条件,能作出唯一△ABC的是( )
A. AB=3,BC=4,CA=8B. AB=4,BC=3,∠A=60°
C. ∠A=60°,∠B=45°,AB=4D. ∠C=90°,∠B=30°,∠A=60°
8.如图,在△ABC中,∠B=34°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1−∠2的度数是( )度.
A. 68B. 58C. 34D. 17
9.如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°;②∠ADE=∠CDE;③DE=BE;④AD=AB+CD,四个结论中成立的是( )
A. ①③B. ①②③C. ②③④D. ①②④
10.如图,点F,C在BE上,AC=DF,BF=EC,AB=DE,AC与DF相交于点G,则与2∠DFE相等的是( )
A. ∠A+∠DB. 3∠BC. 180°−∠FGCD. ∠ACE+∠B
二、填空题:本题共8小题,每小题3分,共24分。
11.已知一个等腰三角形的两边长分别为3、6,则这个三角形的周长是 .
12.在△ABC中,∠A=50°,∠B=∠C=x°,则x的值是 .
13.如图,在△ABC中,∠C=90°,AD平分∠BAC,DC=3,△ABD中AB边上的高是 .
14.已知三角形两边长分别是3cm和7cm,则第三边长a的取值范围是 .
15.如图,在△ABC中,D是AC上一点,CD=2AD,连接BD,CE是△BCD的中线,若△ABC的面积为90,则△BEC的面积为 .
16.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= .
17.如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画 个.
18.如图,在Rt△ABC中,∠ABC=90°,AB=6,∠BAC=30°,∠BAC的平分线交BC于点D,E,F分别是线段AD和AB上的动点,则BE+EF的最小值是 .
三、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
19.(本小题8分)
已知a,b,c是△ABC的三条边,若a,b满足|a−7|+(b−1)2=0,且c为奇数,求△ABC的周长.
20.(本小题8分)
已知,如图,△ABC,∠ACB=90°,∠B=2∠A.
(1)用直尺和圆规作△ABC的角平分线BD,保留作图痕迹;
(2)在(1)的基础上,求∠ADB的度数.
21.(本小题8分)
初一(10)班数学学习小组“孙康映雪”在学习了第七章平面图形的认识(二)后对几何学习产生了浓厚的兴趣.请你认真研读下列三个片断,并完成相关问题.
如图1,直线OM⊥ON,垂足为O,三角板的直角顶点C落在∠MON的内部,三角板的另两条直角边分别与ON、OM交于点D和点B.
【片断一】
(1)小孙说:由四边形内角和知识很容易得到∠OBC+∠ODC的值.如果你是小孙,得到的正确答案应是:∠OBC+∠ODC=_______°.
【片断二】
(2)小康说:连接BD(如图2),若BD平分∠OBC,那么BD也平分∠ODC.请你说明当BD平分∠OBC时,BD也平分∠ODC的理由.
【片断三】
(3)小雪说:若DE平分∠ODC、BF平分∠MBC,我发现DE与BF具有特殊的位置关系.请你先在备用图中补全图形,再判断DE与BF有怎样的位置关系并说明理由.
22.(本小题8分)
如图,DE⊥AC,BF⊥AC,AD=BC,AF=CE,求证:DE=BF.
23.(本小题8分)
已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=50°,AB=AC,AD=AE,连结BD、CE,BD所在直线交CE、AC分别于点F、G.
(1)求证:△BAD≌△CAE;
(2)求∠BFC的度数.
24.(本小题8分)
在△ABC中,BD平分∠ABC交AC于点D,点E是线段AC上的动点(不与点D重合),过点E作EF//BC交射线BD于点F,∠CEF的角平分线所在直线与射线BD交于点G.
(1)如图,点E在线段AD上运动.
①若∠ABC=40°,∠C=60°,则∠BGE的度数是______;
②若∠A=70°,则∠BGE_______;
③探究∠BGE与∠A之间的数量关系,并说明理由;
(2)若点E在线段DC上运动时,∠BGE与∠A之间的数量关系与(1)③中的数量关系是否相同?若不同,请直接写出∠BGE与∠A之间的数量关系,不需说理.
25.(本小题8分)
如图1,在△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,BD=CE,连接ED交BC于F.
(1)求证:DF=EF;
(2)如图2,连接CD,若∠DFB=45°,BC=4,求△BCD的面积.
参考答案
1.【答案】C
【解析】【分析】先根据折叠的性质,得出∠DFE=12∠DFG=50°,再根据CD // AB,可得∠BEF=∠DFE=50°,进而得到∠AEF=130°=∠AˈEF,故∠AˈEB=130°−50°=80°,然后根据角平分线的定义以及平行线的性质,即可得到∠AˈBE=∠BEG=25°,最后在△AˈBE中,根据∠Aˈ=180°−∠AˈBE−∠AˈEB进行计算即可得出结论.
【解答】解:如图所示,连接EG,
∵∠DˈFC=80°,
∴∠DFG=100°,
由折叠可得,∠DFE=12∠DFG=50°,
∵CD // AB,
∴∠BEF=∠DFE=50°,
∴∠AEF=130°=∠AˈEF,
∴∠AˈEB=130°−50°=80°,
又∵EG平分∠FEB,
∴∠BEG=12∠BEF=25°,
∵EG // AˈDˈ,
∴∠AˈBE=∠BEG=25°,
∴△AˈBE中,∠Aˈ=180°−∠AˈBE−∠AˈEB=180°−80°−25°=75°,
由折叠可得∠A=∠Aˈ=75°,
故选:C.
【点评】本题主要考查了折叠的性质,平行线的性质以及角平分线的定义的综合应用,解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
2.【答案】B
【解析】【分析】根据三角形的三边关系确定第三边的取值范围,结合选项解答即可.
【解答】解:设第三边长为a cm,
由三角形的三边关系,得4−2
相关试卷
这是一份2024—2025学年上学期北京初中数学九年级开学模拟试卷2(含答案),共24页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
这是一份2024—2025学年上学期北京初中数学八年级开学模拟试卷2(含答案),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份广东省深圳大学附中2024-2025学年八年级上学期数学开学自测模拟试卷,共15页。









