苏教版 (2019)必修 第二册第12章 复数12.3 复数的几何意义课文配套ppt课件

这是一份苏教版 (2019)必修 第二册第12章 复数12.3 复数的几何意义课文配套ppt课件，共40页。PPT课件主要包含了课前预习，课堂互动，分层训练，内容索引，知识探究，题型剖析，思维升华，课堂小结，素养提升等内容，欢迎下载使用。
熟练掌握复数的代数形式的加、减运算法则，理解复数加、减法的几何意义.
通过本节课的学习，发展数学运算素养及数学抽象素养.
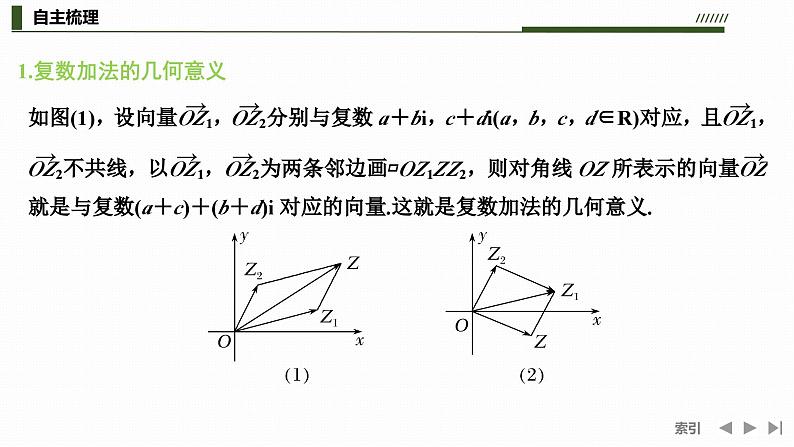
1.复数加法的几何意义
2.复数减法的几何意义
两个复数的差的模就是复平面内与这两个复数对应的______________.
①复数加法的几何意义就是向量加法的平行四边形法则.②复数减法的几何意义就是向量减法的三角形法则.　　　
1.思考辨析，判断正误(1)复数加法的运算法则类同于实数的加法法则.( )(2)复数与复数相加减后结果为复数.( )(3)复数减法的几何意义类同于向量减法运算的几何意义.( )
2.设z1＝3－4i，z2＝－2＋3i，则z1－z2在复平面内对应的点位于(　　)A.第一象限 B.第二象限 C.第三象限 D.第四象限解析　∵z1－z2＝(3－4i)－(－2＋3i)＝5－7i，∴z1－z2在复平面内对应的点位于第四象限.
题型一　复数加、减法的几何意义
【例1】　如图所示，在平行四边形OABC中，顶点O，A，C分别表示复数0，3＋2i，－2＋4i.求：
解　(1)因为0－(3＋2i)＝－3－2i，
题型二　|z－z0|(z，z0∈C)的几何意义
【例2】　复数z满足|z＋3＋4i|＝2，则|z|的最大值是(　　)A.7 B.9 C.3 D.5解析　由题意可知|z－(－3－4i)|＝2，即复数z在复平面内对应的点与复数－3－4i在复平面内对应的点的距离为2，复数z在复平面内对应的点在复平面内的轨迹为如图所示的圆Q，数形结合可知|z|的最大值在点P处取得，
求复数模的最值问题可根据复数模的几何意义数形结合解题.(1)|z－z0|表示复数z，z0在复平面内的对应点之间的距离，在应用时，要把绝对值号内变为两复数差的形式.(2)|z－z0|＝r表示复数z在复平面内对应的点构成以z0在复平面内对应的点为圆心，r为半径的圆.(3)涉及复数模的最值问题以及点的轨迹问题，均可从两点间距离公式的复数表达形式入手进行分析判断，然后通过几何方法进行求解.
A.以(－1，－2)为圆心，4为半径的圆B.以(－1，－2)为圆心，2为半径的圆C.以(1，2)为圆心，4为半径的圆D.以(1，2)为圆心，2为半径的圆解析　设z＝x＋yi，x，y∈R，由题意得z1＝i2 022－2i＝－1－2i，则由|z－z1|＝4，得|(x＋1)＋(y＋2)i|＝4，即(x＋1)2＋(y＋2)2＝42＝16，故复数z在复平面内对应的点P组成的图形是以(－1，－2)为圆心，4为半径的圆.
题型三　复数的模的最值问题
【例3】　(1)如果复数z满足|z＋i|＋|z－i|＝2，那么|z＋i＋1|的最小值是(　　)
解析　设复数－i，i，－1－i在复平面内对应的点分别为Z1，Z2，Z3，因为|z＋i|＋|z－i|＝2，|Z1Z2|＝2，所以点Z的集合为线段Z1Z2，问题转化为：动点Z在线段Z1Z2上移动求|ZZ3|的最小值，因为|Z1Z3|＝1.∴|z＋i＋1|min＝1.
复数模的最值问题最常用的策略有：用函数思想、方程思想可将问题转化为代数法或三角法，用数形结合思想可将问题转化为几何法，用重要的不等式公式可将问题转化为不等式法.
【训练3】　已知|z|＝1且z∈C，求|z－2－2i|(i为虚数单位)的最小值.
解　因为|z|＝1且z∈C，作图如图，所以|z－2－2i|的几何意义为单位圆上的点M到复平面内的点P(2，2)的距离，
一、牢记3个知识点1.复数加法的几何意义.2.复数减法的几何意义.3.复数差的模.二、掌握2种方法——类比法，数形结合三、注意1个易错点　忽略模的几何意义.　　　　　　　　　　　　　　　　　　
一、选择题1.已知复数z满足z＋2i＝12－i，则|z|＝(　　)
解析　∵z＋2i＝12－i，∴z＝12－3i，
A.z1＋z2＋z3＝0 B.z1－z2－z3＝0C.z1－z2＋z3＝0 D.z1＋z2－z3＝0
∴z1＋z2－z3＝0.
解析　由|z1|＝|z2|＝2，|z1＋z2|＝2，及复数加减法的几何意义知以z1，z2所在边为邻边的对应的图形为正方形，
A项，z2 021＝i2 021＝i1＝i，正确；B项，|z＋i|＝|i＋i|＝2，正确；C项，z的共轭复数为－i，正确；
解析　设O为坐标原点，
7.设f(z)＝z－3i＋|z|，若z1＝－2＋4i，z2＝5－i，则f(z1＋z2)＝________.
8.已知复数|z|＝1，则复数3＋4i＋z的模的最大值为________，最小值为________.解析　令ω＝3＋4i＋z，则z＝ω－(3＋4i).∵|z|＝1，∴|ω－(3＋4i)|＝1，
三、解答题9.已知z1，z2∈C，若|z1|＝5，z2＝3＋4i，z1z2是纯虚数，求z1.解　设z1＝a＋bi(a，b∈R)，由z1z2＝(a＋bi)(3＋4i)＝(3a－4b)＋(3b＋4a)i为纯虚数，
又|z1|＝5，∴a2＋b2＝25，②
∴z1＝4＋3i或z1＝－4－3i.
10.已知复数z1＝i(1－i)3.(1)求|z1|；(2)若|z|＝1，求|z－z1|的最大值.解　(1)∵z1＝i(1－i)3＝i(1－i)2(1－i)＝i(－2i)(1－i)＝2(1－i)＝2－2i，
(2)如图所示，由|z|＝1可知，z在复平面内对应的点的轨迹是半径为1，圆心为O(0，0)的圆，而z1对应着坐标系中的点Z1(2，－2).所以|z－z1|的最大值可以看成是点Z1(2，－2)到圆上的点的距离的最大值.
所以点D对应的复数为z＝3＋3i，
13.集合M＝{z||z－1|≤1，z∈C}，N＝{z||z－1－i|＝|z－2|，z∈C}，集合P＝M∩N.指出集合P在复平面内所表示的图形.解　由|z－1|≤1可知，集合M在复平面内所对应的点集是以点E(1，0)为圆心，以1为半径的圆的内部及边界；由|z－1－i|＝|z－2|可知，集合N在复平面内所对应的点集是以点(1，1)和(2，0)为端点的线段的垂直平分线l，因此集合P是圆面截直线l所得的一条线段AB，如图所示.