广西南宁三中青秀校区2024-2025学年九年级上学期开学检测数学试题（原卷版）

这是一份广西南宁三中青秀校区2024-2025学年九年级上学期开学检测数学试题（原卷版），共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

九年级数学
（考试时间：120分钟 满分：120分）
注意：本试卷分试题卷和答题卡（卷）两部分，答案一律填写在答题卡（卷）上，在试题卷上作答无放．
一、选择题（共12小题，每小题3分，共36分，在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑，）
1. 的绝对值是（ ）
A. ﹣2B. 2C. D.
2. 我国近年来大力推进国家教育数字化战略行动，截至2024年6月上旬，上线慕课数量超过7.8万门，学习人次达1290000000建设和应用规模居世界第一．用科学记数法将数据1290000000表示为（ ）
A. B. C. D.
3. 为了解我校初三年级所有同学的数学成绩，从中抽出500名同学的数学成绩进行调查，抽出的500名考生的数学成绩是（ ）
A. 总体B. 样本C. 个体D. 样本容量
4. 下列计算正确的是（ ）
A. B. C. D.
5. 不等关系在生活中广泛存在．如图，、分别表示两位同学的身高，表示台阶的高度．图中两人的对话体现的数学原理是（ ）
A. 若，则B. 若，，则
C. 若，，则D. 若，，则
6. 一只杯子静止在斜面上，其受力分析如图所示，重力方向竖直向下，支持力的方向与斜面垂直，摩擦力的方向与斜面平行．若斜面的坡角，则摩擦力与重力方向的夹角的度数为（ ）
A. B. C. D.
7. 如图，在一块长、宽的矩形耕地上挖三条水渠（水渠的宽都相等），水渠把耕地分成面均为的6个矩形小块，水渠应挖多宽？设水渠应挖xm宽，根据题意，可列方程（ ）
A. B.
C. D.
8. 如图，在中，是边的中点．按下列要求作图：
①以点圆心、适当长为半径画弧，交线段于点，交于点；
②以点为圆心、长为半径画弧，交线段于点；
③以点为圆心、长为半径画弧，交前一条弧于点，点与点在直线同侧；
④作直线，交于点．下列结论不一定成立的是（ ）
A. B.
C. D.
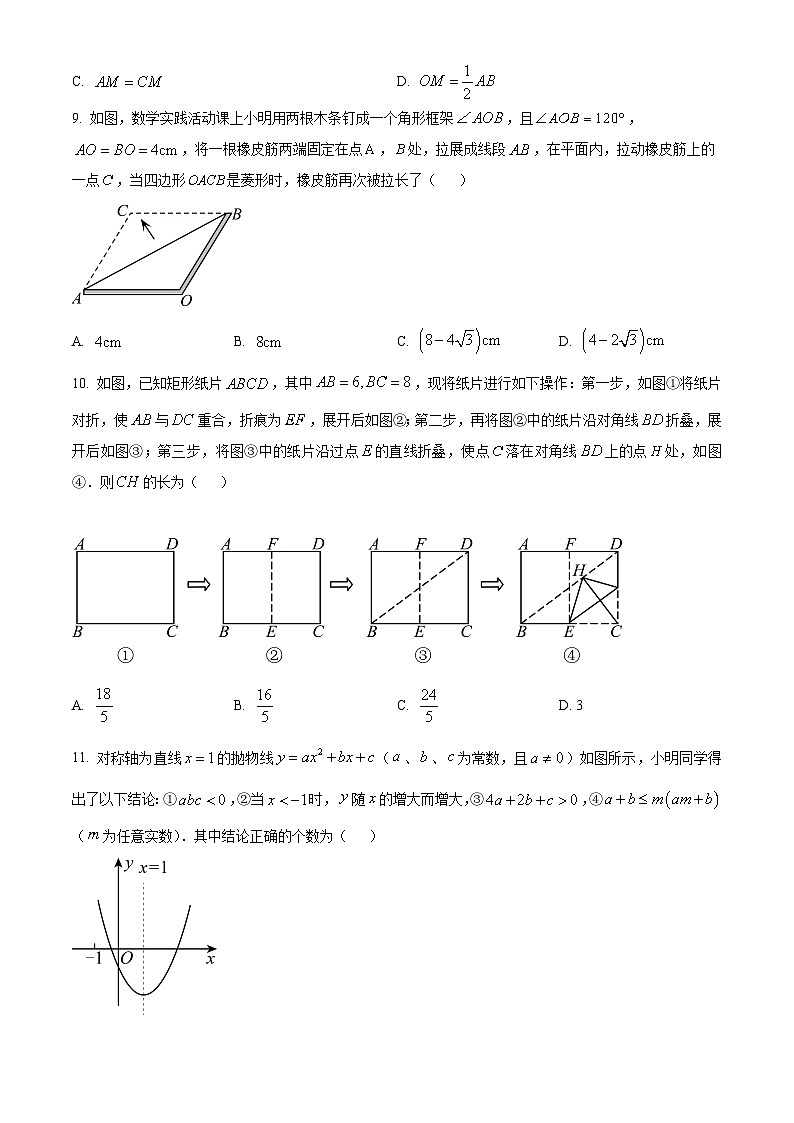
9. 如图，数学实践活动课上小明用两根木条钉成一个角形框架，且，，将一根橡皮筋两端固定在点，处，拉展成线段，在平面内，拉动橡皮筋上的一点，当四边形是菱形时，橡皮筋再次被拉长了（ ）

A. B. C. D.
10. 如图，已知矩形纸片，其中，现将纸片进行如下操作：第一步，如图①将纸片对折，使与重合，折痕为，展开后如图②；第二步，再将图②中的纸片沿对角线折叠，展开后如图③；第三步，将图③中的纸片沿过点的直线折叠，使点落在对角线上的点处，如图④．则的长为（ ）
A. B. C. D. 3
11. 对称轴为直线的抛物线（、、为常数，且）如图所示，小明同学得出了以下结论：①，②当时，随的增大而增大，③，④（为任意实数）．其中结论正确的个数为（ ）
A. 1B. 2C. 3D. 4
12. 如图1，矩形中，为其对角线，一动点从出发，沿着路径行进，过点作，垂足为．设点的运动路程为，为，与的函数图象如图2，则的长为（ ）
A. B. C. D.
二、填空题（本大题共6小题，每小题2分，共12分．请把答案填在答题卷上）
13. 25平方根是_____．
14. 若等腰三角形的一个底角的度数为，则它的顶角度数为_____________°．
15. 若关于x的一元二次方程有两个相等的实数根，则k的值为________．
16. 如图，D，E分别是边，的中点，连接，．若，则的长为__________

17. 飞机着陆后滑行的距离（单位：）关于滑行时间（单位：）的函数解析式是．在飞机着陆滑行中，飞机从开始滑行到停止所需时间为______秒．
18. 如图，在矩形ABCD中，，E，F分别是AD，AB的中点，的平分线交AB于点G，点P是线段DG上的一个动点，则的周长最小值为__________．
三、解答题（本大题共8小题，共72分．解答应写出必要的文字说明、证明过程或演算步骤）
19. 计算：
20. 解方程：
21. 如图，每个小方格都是边长为1个单位长度的正方形，建立如图所示的平面直角坐标系．的三个顶点坐标分别为，，．
（1）填空：面积为 ；
（2）把先向左平移5个单位长度得到，再将沿x轴翻折得到，请在平面直角坐标系中直接画出与；
（3）在（2）的条件下，在x轴上是否存在点P，使的面积是的面积的一半？若存在，求出点P的坐标；若不存在，说明理由．
22. 某卫生局为了了解该市社区医院对患者随访情况，随机抽查了部分社区医院一年来对患者随访的次数，并用得到的数据绘制了如图1、图2所示的两幅不完整的统计图．请根据图中提供的信息，回答下列问题：
（1）这次抽样调查中共抽查了患者___________人，________，众数是________，中位数是_________；
（2）请补全条形统计图；
（3）如果该市社区医院患者有60000人，请你估计“随访的次数不少于7次”社区医院的患者有多少人？
23. 如图，在中，为的中点，四边形是平行四边形，，DE相交于点．
（1）求证：四边形是矩形；
（2）若，，求AD的长．
24. 某条东西方向道路双向共有三条车道，在早晚高峰经常会拥堵，数学研究小组希望改善道路拥堵情况，他们对该路段的交通量（辆分钟）和时间进行了统计和分析，得到下列表格，并发现时间和交通量的变化规律符合一次函数的特征．
（1）请用一次函数分别表示与、与之间的函数关系．（不写定义域）
（2）如图，同学们希望设置可变车道来改善拥堵状况，根据车流量情况改变可变车道的行车方向．单位时间内双向交通总量为，车流量大的方向交通量为，经查阅资料得：当，需要使可变车道行车方向与拥堵方向相同，以改善交通情况．该路段从8时至20时，如何设置可变车道行车方向以缓解交通拥堵，并说明理由．
25. 【课本再现】
（1）如图1，正方形的对角线相交于点，点又是正方形的一个顶点，而且这两个正方形的边长都为1，四边形为两个正方形重叠部分，正方形可绕点转动，则下列结论正确的是 （填序号即可）．
①；②：③四边形的面积总等于；④连接，总有．
【类比迁移】
（2）如图2，矩形的中心是矩形的一个顶点，与边相交于点与边相交于点，连接，矩形可绕着点旋转，猜想之间的数量关系，并进行证明；
【拓展应用】
（3）如图3，在中，，直角的顶点在边的中点处，它的两条边和分别与直线相交于点可绕着点旋转，当时，求线段的长度．
26. 如图，抛物线与轴交于，两点，与轴交于点， 是抛物线上的任意一点（不与点重合），点的横坐标为，拋物线上点与点之间的部分（包含端点）记为图象．
（1）求抛物线的解析式；
（2）若点位于线段上方，求面积的最大值；
（3）若图象的最大值与最小值的差为4，求的取值范围．时间
8时
11时
14时
17时
20时
自西向东交通量（辆分钟）
10
16
22
28
34
自东向西交通量（辆分钟）
25
22
19
16
13