初中数学人教版（2024）九年级上册21.2.1 配方法优质课件ppt

这是一份初中数学人教版（2024）九年级上册21.2.1 配方法优质课件ppt，文件包含142热机的效率原卷版docx、142热机的效率解析版docx等2份课件配套教学资源，其中PPT共0页， 欢迎下载使用。

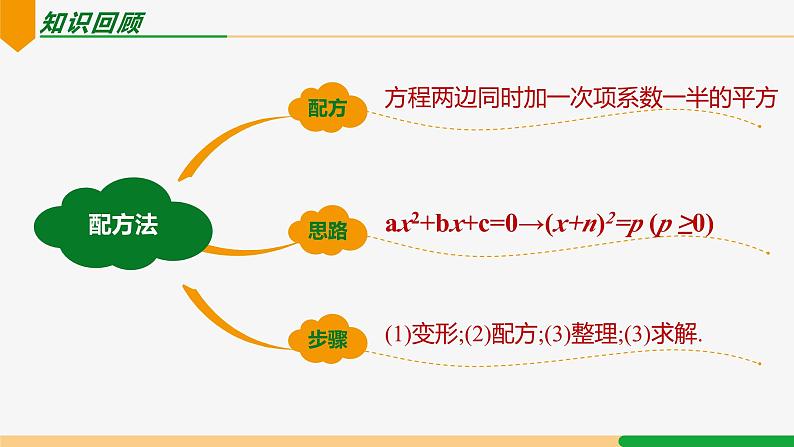
(1)变形;(2)配方;(3)整理;(3)求解.
方程两边同时加一次项系数一半的平方
ax2+bx+c=0→(x+n)2=p (p ≥0)
(6) x2 − x + ___ = ( x − ___)2.
问题1：填空，思考配成完全平方的方法
(3) x2 + 4x + = ( x + )2；
(4) x2 − 6x + = ( x − )2；
(5) x2 + 8x + = ( x + )2；
二次项系数为 1的完全平方式：常数项等于一次项系数一半的平方时
(1) a2 + 2ab + b2 = ( )2；
(2) a2 - 2ab + b2 = ( )2.
例1 若x2-4x+y2+6y+13=0 ，求 (xy)2 的值.
解：对原式配方，得
由非负式的性质可知
x2-4x+4+y2+6y+9=0
(x-2)2+(y+3)2=0
x-2=0 , y+3=0
(xy)2=62=36
例2 用配方法说明：不论 k 取何实数，多项式k2 − 4k＋5 的值必定大于零.
解：k2 − 4k＋5 = k2 − 4k＋4＋1
= (k − 2)2＋1.
因为 (k − 2)2≥0，
所以 k2 − 4k＋5 的值必定大于零.
所以 (k − 2)2＋1≥1＞0.
用配方法求最值.(1) 2x2 − 4x + 5 的最小值； (2) −3x2 + 6x − 7 的最大值.
解：原式 = 2(x −1)2 + 3 当 x = 1 时，有最小值 3.
解：原式= −3(x − 1)2 －4 当 x = 1 时，有最大值− 4.
ax2 + bx + c (a，b，c 均为常数) 型代数式求最值或证明恒为正(负)等问题，都要想到运用配方法，将含字母部分配成 a(x + m)2 + n 的形式来解决.
例3 若 a，b，c 为△ABC 的三边长，且 试判断△ABC 的形状.
解：将原式配方，得
所以，△ABC 为直角三角形.
ax2 + bx + c
a(x + m)2 + n
2. 求最值或证代数式的值恒值为正（负）
1. 完全平方式中的求参数
3. 利用配方构成非负式的和的形式
3. 求最值或证代数式的值最值
1. 若 ，求 (xy)z 的值.
2. 利用配方法证明：不论 x 取何值，代数式 − x2 − x −1 的值总是负数，并求出它的最大值.
解：− x2 − x −1 = −( x2 + x + ) + −1
∴ − x2 − x −1 的值总是负数.
当 时，− x2 − x −1有最大值
3. 已知 a，b，c 为 △ABC 的三边长，且满足等式 ，试判断 △ABC 的形状.
∴ △ABC 为等边三角形.