初中数学人教版（2024）九年级上册21.3 实际问题与一元二次方程教课内容ppt课件

这是一份初中数学人教版（2024）九年级上册21.3 实际问题与一元二次方程教课内容ppt课件，共19页。PPT课件主要包含了实际问题，传播问题，球赛问题，变化率问题，知识要点1，降价促销，进货量为等内容，欢迎下载使用。

a× (1+x)n=b
a× (1±x)n=b
降价促销问题有什么数量关系 ？
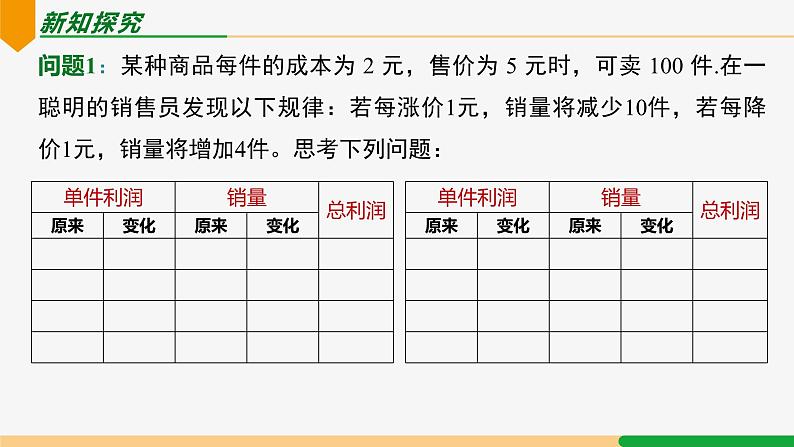
问题1：某种商品每件的成本为 2 元，售价为 5 元时，可卖 100 件.在一聪明的销售员发现以下规律：若每涨价1元，销量将减少10件，若每降价1元，销量将增加4件。思考下列问题：
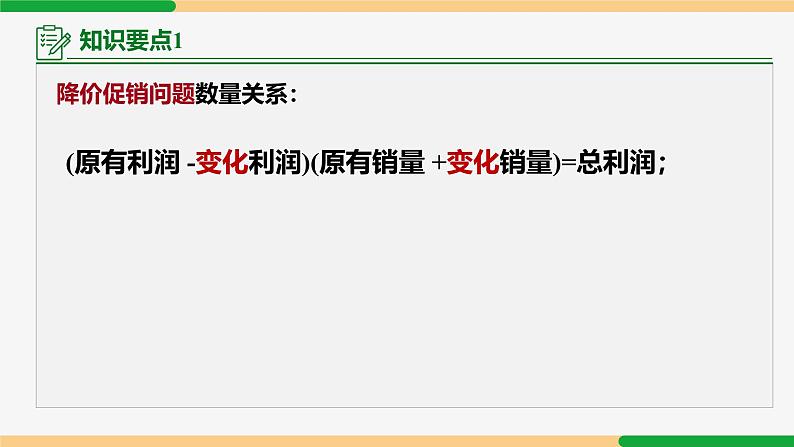
降价促销问题数量关系：
(原有利润 -变化利润)(原有销量 +变化销量)=总利润；
解：设每件衬衫降价 x 元，根据题意得 (40 − x)(20 + 2x) = 1200， 整理得 x2 − 30x + 200 = 0. 解方程得 x1 = 10，x2 = 20. 答：每件衬衫应降价 10 元或 20 元.
例1 某商场销售一批衬衫，平均每天可售出 20 件，每件盈利 40 元．经调查发现，如果每件衬衫降价 1 元，商场平均每天可多售出 2 件．若商场平均每天要盈利1200 元，每件衬衫应降价多少元？
【变式】增加条件：为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施. 若商场平均每天要盈利1200 元，每件衬衫应降价多少元？
解：设每件衬衫降价 x 元，根据题意得 (40 − x)(20 + 2x) = 1200， 整理得，x2 − 30x + 200 = 0. 解方程得，x1 = 10，x2 = 20. 因为要尽快减少库存，所以应取 x = 20. 答：每件衬衫应降价 20 元.
例2 某超市销售一种利润为每千克10元的水产品，一个月能销售出500 kg. 经市场分析，销售单价每涨价1元，月销售量就减少10 kg. 要使得月销售利润达到8 000元，又要“薄利多销”，销售单价应涨价多少元？
解：设销售单价应涨价 x元，由题意，得 (10＋x)(500－10x)＝8 000.解得x1＝10，x2＝30. ∵要“薄利多销”，∴x＝10.答：销售单价应涨价10元.
例3 为促进新旧功能转换，提高经济效益，某科技公司近期研发出一种新型高科技设备，每台设备成本价为25 万元，经过市场调研发现，该设备的月销售量 y (台)和销售单价 x (万元) 满足如图所示的一次函数关系．(1) 求月销售量 y 与销售单价 x 的函数关系式；
(2) 根据相关规定，此设备的销售单价不得高于 35 万元，如果该公司想获得 130 万元的月利润，那么该设备的销售单价应是多少万元？
(2) 依题知 (x − 25)(−5x + 200) = 130，整理方程，得 x2 − 65x + 1026 = 0．解得 x1 = 27，x2 = 38．∵ 此设备的销售单价不得高于 35 万元，∴ x = 38 应舍去，则 x = 27．答：该设备的销售单价应是 27 万元．
解：(1) 设 y 与 x 的函数关系式为 y = kx + b，
所以 y 与 x 的函数关系式为 y = -5x + 200．
1.某种花卉每盆的盈利与每盆的株数有一定的关系，每盆植3株时，平均每株盈利4元；若每盆增加1株，平均每株盈利减少0.5元，要使每盆的盈利达到15元，每盆应多植多少株？设每盆多植x株，则可以列出的方程是（　　）A.(3+x)(4-0.5x)=15 B.(x+3)(4+0.5x)=15 C.(x+4)(3-0.5x)=15 D.(x+1)(4-0.5x)=15
某超市将进货单价为 40 元的商品按 50 元出售时，能卖 500 个，已知该商品要涨价 1 元，其销售量就要减少 10 个，为了赚 8000 元利润，售价应定为多少，这时应进货多少个？
解：设每个商品涨价 x 元，则单件利润为(50 + x - 40)元，销售量为 (500 − 10x) 个，则 (500 − 10x) · (50 + x − 40) = 8000，整理得 x2 − 40x + 300 = 0. 解得 x1 = 10，x2 = 30，都符合题意.当 x = 10 时，50 + x = 60，500 - 10x = 400；当 x = 30 时，50 + x = 80， 500 - 10x = 200.答：要想赚 8000 元，售价应定为 60 元/个，进货 400 个；或售价定为 80 元/个，进货 200 个.
某超市将进货单价为40元的商品按50元出售时，能卖500个，已知该商品要涨价1元，其销售量就要减少10个，为了赚8000元利润，售价应定为多少，这时应进货为多少个？
解：设每个商品涨价x元，则销售价为(50+x)元，销售量为(500－10x)个，则 (500－10x) [(50+x)－40]=8000，整理得 x2－40x+300=0， 解得x1=10，x2=30都符合题意.当x=10时,50+x =60，500－10 x=400；当x=30时，50+x =80， 500－10 x=200.答：要想赚8000元，售价为60元或80元；若售价为60元，则进货量应为400；若售价为80元，则进货量应为200个.
解：设每件衬衫降价x元，根据题意得： （40-x)(20+2x)=1200 整理得，x2-30x+200=0 解方程得，x1=10,x2=20 因为要尽快减少库存，所以x=10舍去.答：每件衬衫应降价20元.
某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫降价1元，商场平均每天可多售出2件，若商场平均每天要盈利1200元，每件衬衫应降价多少元？
某商城在销售中发现：“宝宝乐”牌童装平均每天可售出20件，每件盈利40元.为了迎接”十一”国庆节,商场决定采取适当的降价措施.经调查发现,如果每件童装降价4元，那么平均每天就可多售出8件.要想平均每天盈利1200元,那么每件童装应该降价多少元?
解：设每件童装应降价x元，每件童装的利润 (40- x）元，每天销售的童装件数（20+2x)件，根据题意，得 (40- x)(20+2x)=1200 化简得 x2 -30 x+200=0 解得x1=20，x2=10 因为尽快减少库存，所以x2=10 答：每件童装应降价20元.
2. 某商店从厂家以每件21元的价格购进一批商品,若每件商品售价为x元,则每天可卖出(350-10x)件,但物价局限定每件商品加价不能超过进价的20%.商店要想每天赚400元,需要卖出多少件商品?每件商品的售价应为多少元?
3.某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.市场调研表明:当销售价为每上涨1元时,其销售量就将减少10个.商场要想销售利润平均每月达到10000元,每个台灯的定价应为多少元?这时应进台灯多少个?
定价为40+10=50元或40+40=80元