2023-2024学年福建省泉州五中九年级（上）期中数学试卷（有答案）

这是一份2023-2024学年福建省泉州五中九年级（上）期中数学试卷（有答案），共20页。

A．B．C．D．
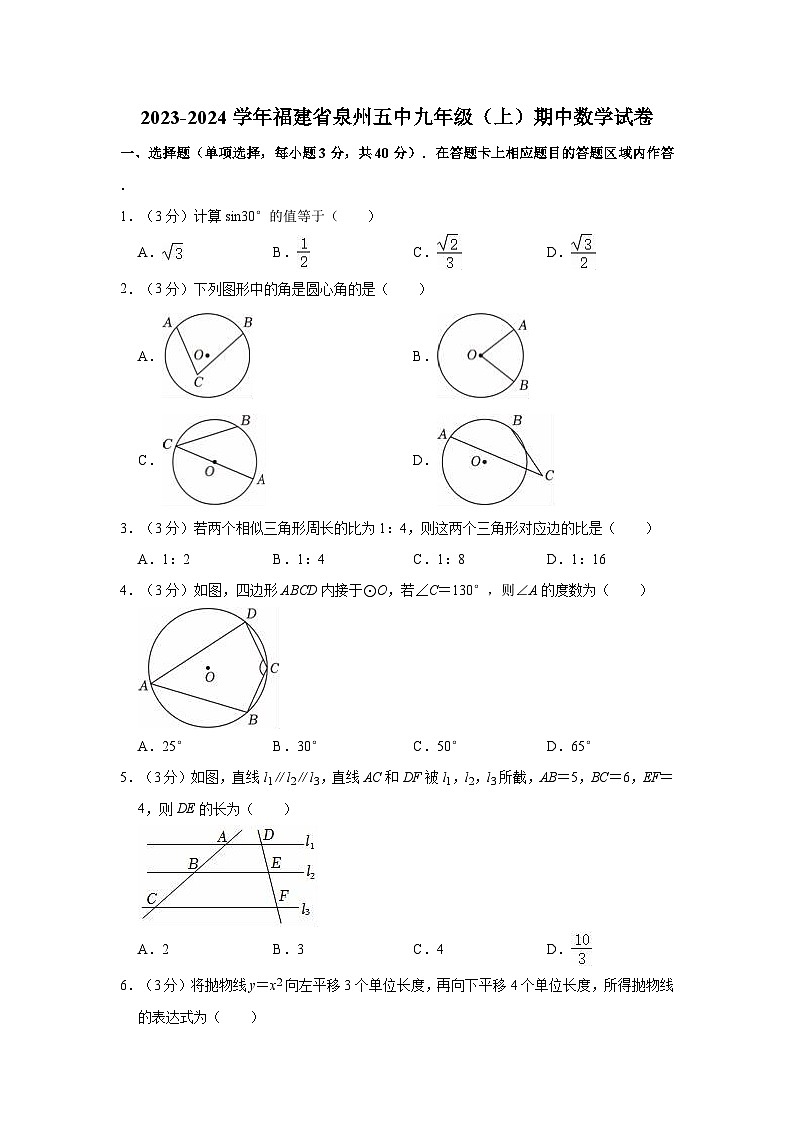
2．（3分）下列图形中的角是圆心角的是（ ）
A．B．
C．D．
3．（3分）若两个相似三角形周长的比为1：4，则这两个三角形对应边的比是（ ）
A．1：2B．1：4C．1：8D．1：16
4．（3分）如图，四边形ABCD内接于⊙O，若∠C＝130°，则∠A的度数为（ ）
A．25°B．30°C．50°D．65°
5．（3分）如图，直线l1∥l2∥l3，直线AC和DF被l1，l2，l3所截，AB＝5，BC＝6，EF＝4，则DE的长为（ ）
A．2B．3C．4D．
6．（3分）将抛物线y＝x2向左平移3个单位长度，再向下平移4个单位长度，所得抛物线的表达式为（ ）
A．y＝（x+3）2+4B．y＝（x﹣3）2﹣4
C．y＝（x﹣3）2+4D．y＝（x+3）2﹣4
7．（3分）在Rt△ABC中，∠C＝90°，若，AC＝1，则tanB的值为（ ）
A．B．2C．D．
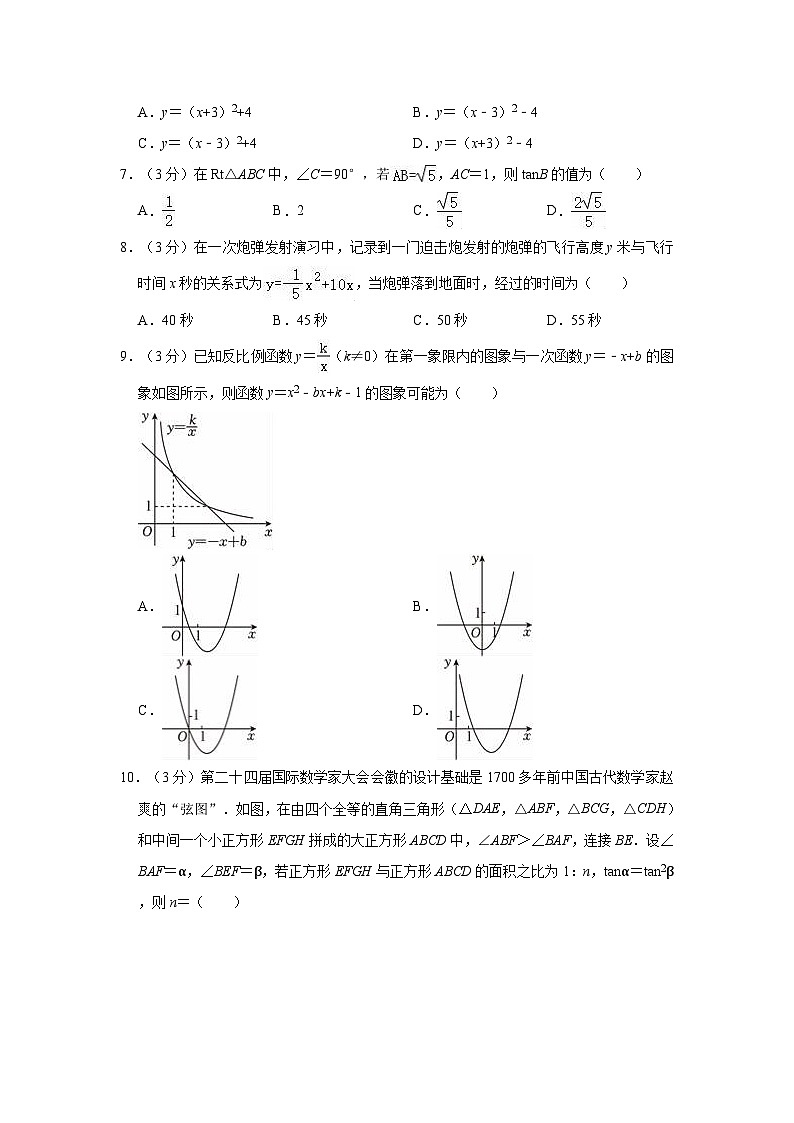
8．（3分）在一次炮弹发射演习中，记录到一门迫击炮发射的炮弹的飞行高度y米与飞行时间x秒的关系式为，当炮弹落到地面时，经过的时间为（ ）
A．40秒B．45秒C．50秒D．55秒
9．（3分）已知反比例函数y＝（k≠0）在第一象限内的图象与一次函数y＝﹣x+b的图象如图所示，则函数y＝x2﹣bx+k﹣1的图象可能为（ ）
A．B．
C．D．
10．（3分）第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”．如图，在由四个全等的直角三角形（△DAE，△ABF，△BCG，△CDH）和中间一个小正方形EFGH拼成的大正方形ABCD中，∠ABF＞∠BAF，连接BE．设∠BAF＝α，∠BEF＝β，若正方形EFGH与正方形ABCD的面积之比为1：n，tanα＝tan2β，则n＝（ ）
A．5B．4C．3D．2
二、填空题（每小题4分，共24分）．在答题卡上相应题目的答题区域内作答．
11．（4分）已知＝，那么的值为 ．
12．（4分）已知某斜坡AB的坡度i＝1：1，则斜坡AB的坡角α的大小为 °．
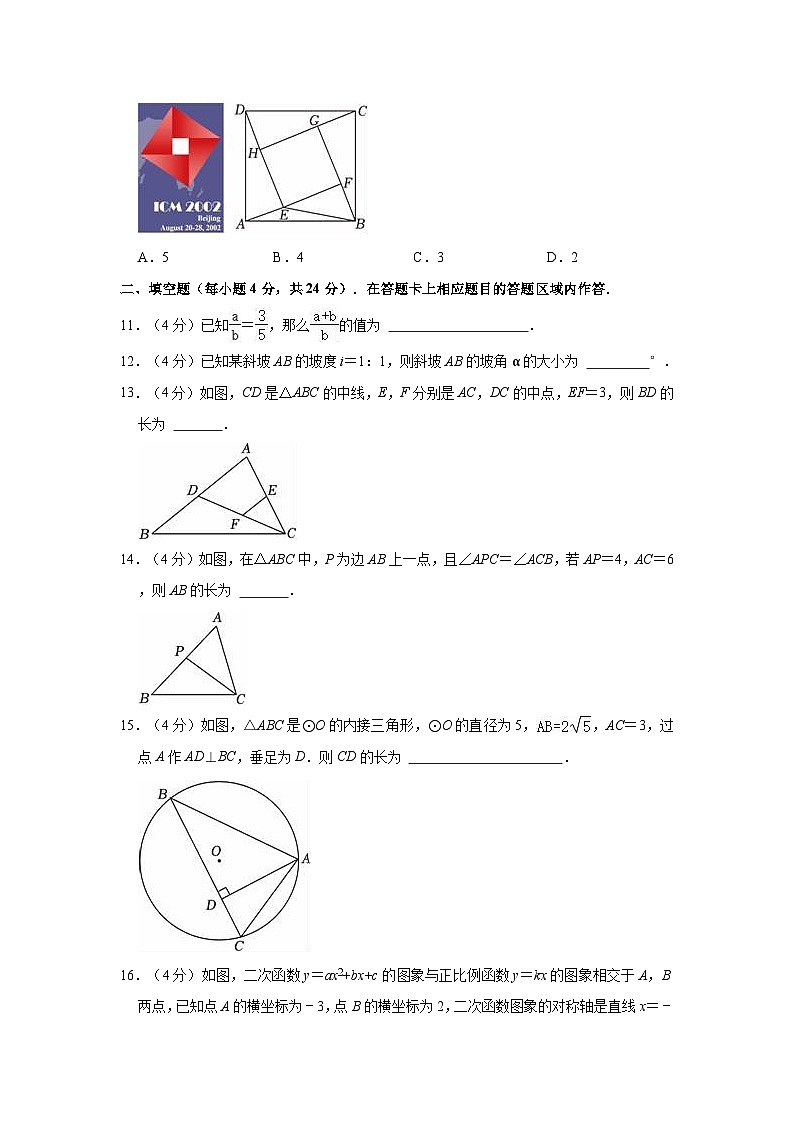
13．（4分）如图，CD是△ABC的中线，E，F分别是AC，DC的中点，EF＝3，则BD的长为 ．
14．（4分）如图，在△ABC中，P为边AB上一点，且∠APC＝∠ACB，若AP＝4，AC＝6，则AB的长为 ．
15．（4分）如图，△ABC是⊙O的内接三角形，⊙O的直径为5，，AC＝3，过点A作AD⊥BC，垂足为D．则CD的长为 ．
16．（4分）如图，二次函数y＝ax2+bx+c的图象与正比例函数y＝kx的图象相交于A，B两点，已知点A的横坐标为﹣3，点B的横坐标为2，二次函数图象的对称轴是直线x＝﹣1．下列结论：①abc＜0；②3b+2c＞0；③关于x的方程ax2+bx+c＝kx的两根为x1＝﹣3，x2＝2；④k＝a．其中正确的是 .（只填写序号）
三、解答题（共86分）．在答题卡上相应题目的答题区域内作答．
17．（8分）计算：．
18．（8分）如图，∠BAD＝∠CAE，∠B＝∠D．求证：△ABC∽△ADE．
19．（18分）如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（3，1），B（1，2），C（4，3）以原点O为位似中心，在第一象限内画出△ABC的位似图形△A1B1C1，使它与△ABC的相似比为2：1．
20．（8分）已知关于x的二次函数y＝x2﹣（m﹣2）x﹣3，该函数图象经过点A（2，﹣3）．
（1）求这个二次函数的表达式及顶点B的坐标；
（2）若这个二次函数图象与y轴的交点为C，请直接写出△ABC的面积．
21．（9分）2023年5月30日9点31分，“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射，成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站．如图，在发射的过程中，飞船从地面O处发射，当飞船到达A点时，从位于地面C处的雷达站测得AC的距离是8km，仰角为30°；10s后飞船到达B处，此时测得仰角为45°．
（1）求点A离地面的高度AO；
（2）求飞船从A处到B处的平均速度．（结果精确到0.1km/s，参考数据：≈1.73）
22．（9分）如图，OA＝OB，AB交⊙O于点C，D，OE是半径，且OE⊥AB于点F．
（1）求证：AC＝BD．
（2）若OF＝2EF，CD＝8，求⊙O直径的长．
23．（10分）某工厂计划从现在开始，在每个生产周期内生产并销售完某型号设备，该设备的生产成本为10万元/件．设第x个生产周期设备的售价为z万元/件，售价z与x之间的函数解析式是，其中x是正整数．当x＝16时，z＝14；当x＝20时，z＝13．
（1）求m，n的值；
（2）设第x个生产周期生产并销售完设备的数量为y件，且y与x满足关系式y＝5x+20．当12＜x≤20时，工厂第几个生产周期获得的利润最大？最大的利润是多少万元？
24．（12分）在平行四边形ABCD中（顶点A，B，C，D按逆时针方向排列），AB＝24，AD＝20，∠B为锐角，且．（1）如图1，求AB边上的高CH的长；
（2）P是边AB上的一动点，C，D点，同时绕点P按逆时针方向旋转90°得点C′，D′，
①如图2，当C′落在射线CA上时，求BP的长；
②当△AC′D′是直角三角形时，请直接写出BP的长．
25．（14分）已知抛物线y＝﹣x2+bx+c（b，c为常数，c＞1）的顶点为P，与x轴相交于A，B两点（点A在点B的左侧），与y轴相交于点C，抛物线上的点M的横坐标为m，且，过点M作MN⊥AC，垂足为N．
（1）若b＝﹣2，c＝3．
①点P坐标为 ；点A的坐标为 ；
②点G为抛物线y＝﹣x2+bx+c对称轴上的一点，则GB+GC的最小值为 ；
③当时，求m的值；
（2）若点A的坐标为（﹣c，0），且MP∥AC，当时，求点M的坐标．
2023-2024学年福建省泉州五中九年级（上）期中数学试卷
参考答案与试题解析
一、选择题（单项选择，每小题3分，共40分）．在答题卡上相应题目的答题区域内作答．
1．【解答】解：sin30°＝，
故选：B．
2．【解答】解：由圆心角的定义得到：A、C、D图形的角不是圆心角，故A、C、D不符合题意；
B图形中的角是圆心角，故B符合题意．
故选：B．
3．【解答】解：∵两个相似三角形周长的比为1：4，
∴这两个三角形对应边的比为1：4，
故选：B．
4．【解答】解：∵四边形ABCD内接于⊙O，
∴∠C+∠A＝180°，
∵∠C＝130°，
∴∠A＝50°，
故选：C．
5．【解答】解：∵直线l1∥l2∥l3，
∴＝，
∵AB＝5，BC＝6，EF＝4，
∴＝，
∴DE＝，
故选：D．
6．【解答】解：根据题意可得，抛物线平移后的解析式为：y＝（x+3）2﹣4，
故选：D．
7．【解答】解：在Rt△ABC中，∠C＝90°，，AC＝1，
∴BC＝＝＝2，
∴tanB＝＝，
故选：A．
8．【解答】解：在y＝﹣x2+10x中，令y＝0得：
0＝﹣x2+10x，
解得x＝0（舍去）或x＝50，
∴当炮弹落到地面时，经过的时间为50秒；
故选：C．
9．【解答】解：∵一次函数y＝﹣x+b的图象经过第一、二、四象限，且与y轴交于正半轴，则b＞0，反比例函数y＝的图象经过第一、三象限，则k＞0，
∴函数y＝x2﹣bx+k﹣1的图象开口向上，对称轴为直线x＝＞0，
由图象可知，反比例函数y＝与一次函数y＝﹣x+b的图象有两个交点（1，k）和（k，1），
∴﹣1+b＝k，
∴k﹣b＝﹣1，
∴b＝k+1，
∴对于函数y＝x2﹣bx+k﹣1，当x＝1时，y＝1﹣b+k﹣1＝﹣1，
∴函数y＝x2﹣bx+k﹣1的图象过点（1，﹣1），
∵反比例函数y＝与一次函数y＝﹣x+b的图象有两个交点，
∴方程＝﹣x+b有两个不相等的实数根，
∴Δ＝b2﹣4k＝（k+1）2﹣4k＝（k﹣1）2＞0，
∴k﹣1≠0，
∴当x＝0时，y＝k﹣1≠0，
∴函数y＝x2﹣bx+k﹣1的图象不过原点，
∴符合以上条件的只有A选项．
故选：A．
10．【解答】解：设AE＝a，DE＝b，则BF＝a，AF＝b，
∵tanα＝，tanβ＝，tanα＝tan2β，
∴，
∴（b﹣a）2＝ab，
∴a2+b2＝3ab，
∵a2+b2＝AD2＝S正方形ABCD，（b﹣a）2＝S正方形EFGH，
∴S正方形EFGH：S正方形ABCD＝ab：3ab＝1：3，
∵S正方形EFGH：S正方形ABCD＝1：n，
∴n＝3．
故选：C．
二、填空题（每小题4分，共24分）．在答题卡上相应题目的答题区域内作答．
11．【解答】解：∵＝，
∴＝+1
＝+1
＝，
故答案为：．
12．【解答】解：∵斜坡AB的坡度i＝1：1，坡角为α，
∴tanα＝1，
∴α＝45°，
故答案为：45．
13．【解答】解：∵点E，F分别是AC、DC的中点，
∴EF是△ACD的中位线，
∴AD＝2EF＝6，
∵CD是△ABC的中线，
∴BD＝AD＝6；
故答案为：6．
14．【解答】解：∵∠A＝∠A，∠APC＝∠ACB，
∴△ACP∽△ABC，
∴＝，
∵AP＝4，AC＝6，
∴62＝4AB，
∴AB＝9，
故答案为：9．
15．【解答】解：作直径AE，连接BE，如图，
∵AE为⊙O的直径，
∴∠ABE＝90°，
在Rt△ABE中，BE＝＝＝，
∵AD⊥BC，
∴∠ADC＝90°，
∴∠ABE＝∠ADC，
∵∠C＝∠E，
∴△ACD∽△AEB，
∴＝，即＝
解得CD＝．
故答案为：．
16．【解答】解：由图象可得，a＞0，c＜0，又﹣＝﹣1，
∴b＞0．
∴abc＜0．
∴①正确．
由题意，令ax2+bx+c＝kx，
∴ax2+（b﹣k）x+c＝0．
又二次函数y＝ax2+bx+c的图象与正比例函数y＝kx的图象相交于A，B两点，已知点A的横坐标为﹣3，点B的横坐标为2，
∴ax2+（b﹣k）x+c＝0的两根之和为﹣3+2＝﹣1，两根之积为﹣3×2＝﹣6．
∴﹣＝﹣1，＝﹣6．
∴6a+c＝0．
又b＝2a，
∴3b+c＝0．
∴3b+2c＝c＜0．
∴②错误，③正确．
∵﹣＝﹣1，b＝2a，
∴k＝a．
∴④错误．
故答案为：①③．
三、解答题（共86分）．在答题卡上相应题目的答题区域内作答．
17．【解答】解：
＝1+﹣×
＝1+﹣1
＝．
18．【解答】证明：∵∠BAD＝∠CAE，
∴∠BAC＝∠DAE，
∵∠D＝∠B，
∴△ABC∽△ADE．
19．【解答】解：如图所示，△A1B1C1即为所求．
20．【解答】解：（1）∵该二次函数图象经过点A（2，﹣3），
∴﹣3＝22﹣（m﹣2）×2﹣3，
解得：m＝4．
∴二次函数的表达式为y＝x2﹣2x﹣3，
∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，
∴二次函数顶点B点坐标为（1，﹣4）；
（2）由抛物线的表达式知，点C（0，﹣3），
则AC∥x轴，如下图；
则△ABC的面积＝AC×（yA﹣yB）＝2×（﹣3+4）＝1．
21．【解答】解：（1）在Rt△AOC中，∵∠AOC＝90°，∠ACO＝30°，AC＝8km，
∴AO＝AC＝（km），
（2）在Rt△AOC中，∵∠AOC＝90°，∠ACO＝30°，AC＝8km，
∴OC＝AC＝4（km），
在Rt△BOC中，∵∠BOC＝90°，∠BCO＝45°，
∴∠BCO＝∠OBC＝45°，
∴OB＝OC＝4（km），
∴AB＝OB﹣OA＝（4）km，
∴飞船从A处到B处的平均速度＝≈0.3（km/s）．
22．【解答】（1）证明：∵OE⊥AB，且OE过圆心O
∴CF＝DF，
∵OA＝OB，OE⊥AB，
∴AF＝BF，
∴AF﹣CF＝BF﹣DF，
∴AC＝BD
（2）解：连接OC，设⊙O的半径是r，
∵OF＝2EF，OF+EF＝OE＝r，
∴，
∵CD＝8，
∴，
∴，
∴或（舍去），
∴⊙O的直径是．
23．【解答】解：（1）根据题意，把x＝16时，z＝14；x＝20时，z＝13代入y＝mx+n得：
，
解得m＝﹣，n＝18；
（2）设第x个生产周期创造的利润为w万元，
当12＜x≤20时，z＝﹣x+18，
∴w＝（﹣x+18﹣10）（5x+20）
＝﹣x2+35x+160
＝﹣（x﹣14）2+405，
∵﹣＜0，12＜x≤20，
∴当x＝14时，w取得最大值，最大值为405，
∴工厂第14个生产周期获得的利润最大，最大的利润是405万元．
24．【解答】解：（1）在▱ABCD中，BC＝AD＝20，
在Rt△BCH中，sinB＝＝，
∴CH＝BC•sinB＝16；
（2）①如图2，作 CH⊥BA 于点H，
由（1）得，BH＝＝＝12，
作C'Q⊥BA交BA延长线于点Q，则∠CHP＝∠PQC'＝90°，
∴∠C'PQ+∠PC'Q＝90°，
∵∠C'PQ+∠CPH＝90°，
∴∠PC'Q＝∠CPH，
由旋转知，PC'＝PC，
∴△PQC′≌△CHP（AAS），
∴PQ＝CH＝16，
设BP＝x，C′Q＝PH＝12﹣x，QA＝PQ﹣PA＝x﹣8，
∵C′Q⊥AB，CH⊥AB，
∴C′Q∥CH，
∴△AQC′∽△AHC，
∴＝，
∴＝，
∴x＝，
∴BP＝；
②∵点C、D同时绕点P按逆时针方向旋转90°得点C、D'，
∴△PCD≌△PC′D′，CD＝C'D'，CD⊥CD'，
∵AB∥CD，
∴C'D'⊥AB，
情况一：当以C′为直角顶点时，如图．
∵C'D'⊥AB，
∴C′落在线段BA延长线上，
∵PC⊥PC'，
∴PC⊥AB，
由（1）知，PC＝16，BP＝12．
情况二：当以A为直角顶点时，如图，
设C'D'与射线BA的交点为T，
作CH⊥AB于点H．
∵PC⊥PC'，
∴∠CPH+∠TPC'＝90°，
∵点C，D同时绕点P按逆时针方向旋转90°得点C'，D'，
∴∠CPD＝∠C'PD'＝90°，PC＝PD，PC'＝PD'，
∴∠CPD＝∠C'PD'，
∴△PCD≌△PC'D'（SAS），
∴∠PCD＝∠PC'D'，
∵AB∥CD，
∴∠BPC＝∠PCD＝∠PC'D'，
∵∠C'PT+∠CPB＝90°，
∴∠C'PT+∠PC'T＝90°，
∴∠PTC'＝90°＝∠CHP，
∴△CPH≌△PC′T（AAS），
∴C′T＝PH，PT＝CH＝16，
设C′T＝PH＝t，则AP＝12﹣t，
∴AT＝PT﹣PA＝4+t，
∵∠C'AD'＝90°，C'D'⊥AB，
∴△ATD′∽△C′TA，
∴＝，
∴AT2＝C'T•TD'，
∴（4+t）2＝t（24﹣t），
化简得t2﹣8t+8＝0，
解得，t＝4±2，
∴BP＝BH+HP＝12±2，
情况三：当以D'为直角顶点时，
点P落在BA的延长线上，不符合题意．
综上所述，BP＝12或16±2．
25．【解答】解：（1）①∵b＝﹣2，c＝3，
∴抛物线的解析式为y＝﹣x2﹣2x+3＝﹣（x+1）2+4，
∴P（﹣1，4），
当y＝0时，﹣x2﹣2x+3＝0，
解得x1＝﹣3，x2＝1，
∵点A在点B的左侧，
∴A（﹣3，0）．
故答案为：（﹣1，4），（﹣3，0）；
②如图，连接AC交于点G，则此时GB+GC最小，
∵顶点P（﹣1，4），
∴抛物线的对称轴为直线x＝﹣1，
∵A、B关于对称轴对称，
∴AG＝BG，
∴AG+CG＝BG+CG≥AC，
∴当A、C、G三点共线时，GB+GC最小，
∵抛物线的解析式为y＝﹣x2﹣2x+3，与y轴相交于点C，
∴C（0，3），
∴GB+GC＝AG+CG＝AC＝3，
故答案为：3；
③如图，过点M作ME⊥x轴于点E，于直线AC交于点F，
∵A（﹣3，0），C（0，3），
∴OA＝OC，
∴在Rt△AOC中，∠OAC＝45°，
∴在Rt△AEF中，EF＝AE，
∵抛物线y＝﹣x2﹣2x+3上的点M的横坐标为m，其中﹣c＜m＜，
∴﹣3＜m＜﹣1，
∴M（m，﹣m2﹣2m+3），E（m，0），
∴EF＝AE＝m﹣（﹣3）＝m+3，
∴F（m，m+3），
∴FM＝（﹣m2﹣2m+3）﹣（m+3）＝﹣m2﹣3m，
∵A（﹣3，0），C（0，3），
∴∠CAE＝45°，
在Rt△FMN中，∠AFE＝∠MFN＝∠CAE＝45°，
∴FM＝MN＝×＝，
∴﹣m2﹣3m＝，
解得m1＝，m2＝（舍去），
∴m的值为；
（2）∵点A（﹣c，0）在抛物线y＝﹣x2+bx+c上，其中c＞1，
∴﹣c2﹣bc+c＝0，
解得b＝1﹣c，
∴抛物线的解析式为y＝﹣x2+（1﹣c）x+c，
∴M（m，﹣m2+（1﹣c）m+c），其中﹣c＜m＜，
∴顶点P的坐标为（，），对称轴为直线l：x＝．
如图，过点M作MQ⊥l于点Q，连接MP，
则∠MQP＝90°，Q（，﹣m2+（1﹣c）m+c），
∵MP∥AC，
∴∠QPM＝45°，
∴MQ＝QP，
∴﹣m＝﹣[﹣m2+（1﹣c）m+c]，
即（c+2m）2＝1，
解得c1＝﹣2m﹣1，c2＝﹣2m+1（舍去），
同②，过点M作ME⊥x轴于点E，与直线AC交于点F，
则点E（m，0），点F（m，﹣m﹣1），点M（m，m2﹣1），
∴AN+3MN＝AF+FN+3MN＝EF+2FM＝9，
∴（﹣m﹣1）+2（m2−1+m+1）＝9，
即2m2+m﹣10＝0，
解得m1＝﹣，m2＝2（舍去），
∴点M的坐标为（﹣，）．