

2023-2024学年广东省广州市黄埔区苏元学校九年级(上)月考数学试卷(12月份)
展开本试卷分选择题和非选择题两部分,共25小题,满分120分,考试时间120分钟.
第一部分(选择题 共30分)
学校:______姓名:_______班级:______考号:______
一、选择题(每小题3分,共10题,满分30分.在每小题给出的四个选项,只有一项符合题目要求.)
1.下列图形中,既是中心对称图形又是轴对称图形的是·( )
A.B.
C.D.
2.下列事件中,为必然事件的是( )
A.购买一张彩票,中奖B.一个袋中只装有2个黑球,从中摸出一个球是黑球
C.抛掷一枚硬币,正面向上D.打开电视,正在播放广告
3.用配方法解方程,下列变形正确的是( )
A.B.C.D.
4.如图,二次函数的图象与x轴交于A,两点,则下列说法正确的是( )
A.B.点A的坐标为
C.当时,y随x的增大而减小D.图象的对称轴为直线
5.如图,学校课外生物小组试验园地的形状是长40米、宽34米的矩形,为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为960平方米.则小道的宽为多少米?若设小道的宽为x米,则根据题意,列方程为( )
A.B.
C.D.
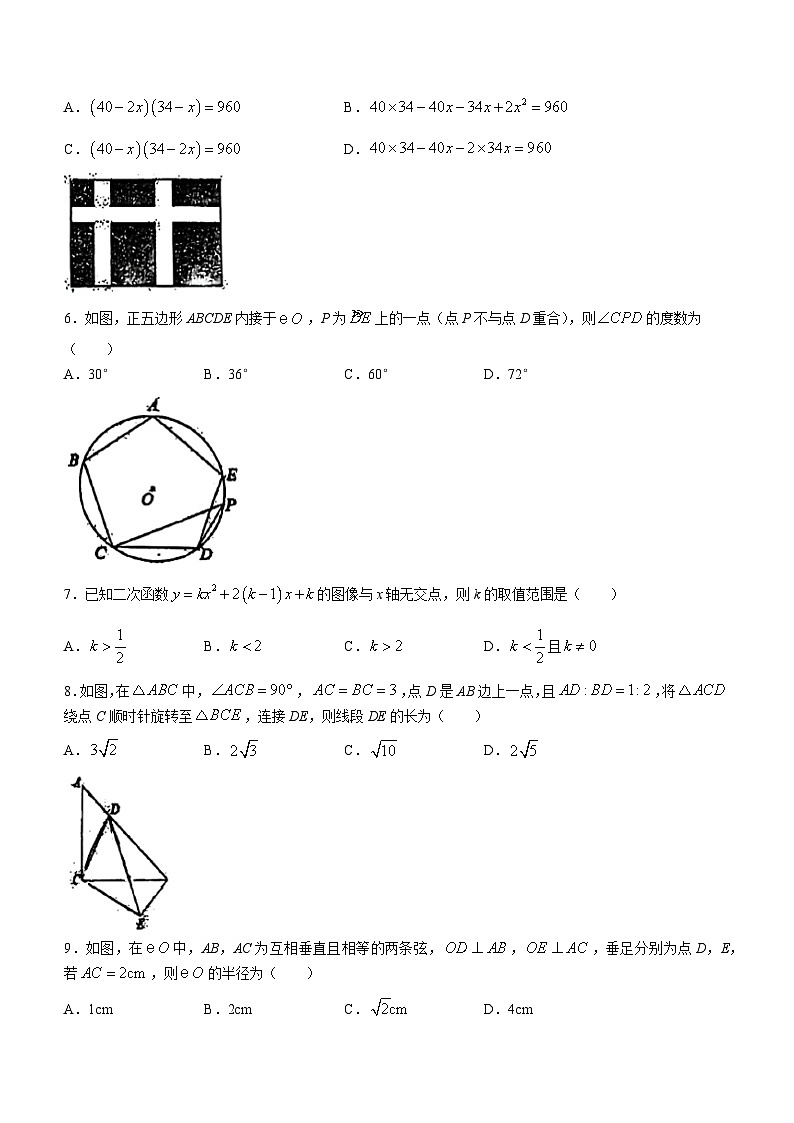
6.如图,正五边形ABCDE内接于,P为上的一点(点P不与点D重合),则的度数为( )
A.30°B.36°C.60°D.72°
7.已知二次函数的图像与x轴无交点,则k的取值范围是( )
A.B.C.D.且
8.如图,在中,,,点D是AB边上一点,且,将绕点C顺时针旋转至,连接DE,则线段DE的长为( )
A.B.C.D.
9.如图,在中,AB,AC为互相垂直且相等的两条弦,,,垂足分别为点D,E,若,则的半径为( )
A.1cmB.2cmC.D.4cm
10.如图,直线与y轴交于点A,与直线交于点B,若抛物线的顶点在直线上移动,且与线段AB、BO都有公共点,则h的取值范围是( )
A.B.C.D.
第二部分 非选择题(共90分)
二.填空题(本题共有6小题,每小题3分,共18分)
11.如图,四边形ABCD内接于,若,则______.
12.有5张仅有编号不同的卡片,编号分别是1,2,3,4,5.从中随机抽取一张,编号是偶数的概率等于______.
13.建设美图城市,改造老旧小区.某市2019年投入资金1000万元,2021年投入资金1440万元,现假定每年投入资金的增长率相同.设该市改造老旧小区投入资金的年平均增长率为x,则所列方程为______.
14.如图为一个的三角板,,小洋同学将三角板绕AC旋转一周,则所得到的几何体的侧面积为______.(结果保留).
15.二次函数,当时,y的取值范围为______.
16.已知在平面直角坐标系中,,,点P在x轴上运动,当点P与点A,B,C三点中任意两点构成直角三角形时,点P的坐标为______.
三.解答题(共9小题,满分72分,解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分4分)解一元二次方程:.
18.(本小题满分6分)如图,方格纸中每个小正方形的边长都是1个单位长度,在平面直角坐标系中的位置如图所示.
(1)将向上平移3个单位后,得到,请画出,并直接写出点的坐标;
(2)将绕点O顺时针旋转90°,请画出旋转后的,并求点B所经过的路径长(结果保留)
19.(本小题满分6分)如图,是绕O点旋转40°后所得的图形,点C恰好在AB上,,求的度数.
20.(本小题满分6分)
一个不透明的口袋中装有红、白两种颜色的小球,这些球除颜色外其他均相同,其中白球有1个.若从中随机摸出一个球,这个球是红球的概率为.
(1)求袋子中红球的个数(请通过列式或列方程解答);
(2)随机摸出两个球,求两次摸到不同颜色小球的概率.
21.(本小题满分8分)
2021年随着神舟十二号飞船搭载“太空出差三人组”成功返回地球,航天模型、航天玩具引起青少年的追捧.某公司今年国庆期间在网络平台上进行直播销售神舟飞船纪念章,已知神舟飞船纪念章的成本价格为8元/枚,经销售发现:每日销售量y(枚)与销售单价x(元/枚)满足一次函数关系,销售单价不低于成本价且不高于20元枚.下表记录的是有关数据,设公司销售神舟飞船纪念章的日获利为w(元)
(1)请求出日销售量y与销售单价x之间的函数关系式;
(2)当销售单价定为多少时,销售这种神舟飞船纪念章的日获利w最大?最大利润为多少元?
22.(本小题满分8分)
已知关于x的一元二次方程,其中a,b,c为的三边.
(1)若是方程的根,判断的形状,并说明理由;
(2)若方程有两个相等的实数根,判断的形状,并说明理由.
23.(本小题满分10分)
如图,,,点O在AB上,交CO延长线于点D,,以点O为圆心,OB为半径作圆.
(1)求证:AC是的切线;
(2)已知,,求OC的长.
24.(本小题满分12分)
如图,抛物线过点,且与直线交于B.C两点,点B的坐标为.
(1)求抛物线的解析式;
(2)点D为抛物线上位于直线BC上方的一点,过点D作轴交直线BC于点E,点P为对称轴上一动点,当线段DE的长度最大时,求的最小值;
(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
25.(本小题满分12分)
在正方形ABCD中,边长为2.点E是线段BC上的动点,以AE为直角边在直线BC的上方作等腰直角三角形AEF,,其中EF交CD于点P,AF交CD于点Q,连接CF.
(1)如图,①若时,求线段CF的长;
②当点E在线段BC上运动时,求证:;
(2)如图,过点B作交EQ于点G,过点D作所在的直线于点H,求HG的最小值.
x(元/枚)
9
10
11
y(枚)
2100
2000
1900
2023-2024学年广东省广州市番禺区仲元中学附属学校九年级(下)月考数学试卷(3月份)(含解析): 这是一份2023-2024学年广东省广州市番禺区仲元中学附属学校九年级(下)月考数学试卷(3月份)(含解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年广东省广州市黄埔区九年级(上)期末数学试卷(A卷)(含详细答案解析): 这是一份2022-2023学年广东省广州市黄埔区九年级(上)期末数学试卷(A卷)(含详细答案解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年广东省广州市黄埔区天键学校九年级(上)期中数学试卷(含解析): 这是一份2023-2024学年广东省广州市黄埔区天键学校九年级(上)期中数学试卷(含解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












