鲁教版（五四学制）（2024）八年级上册3 三角形的中位线优秀课件ppt

这是一份鲁教版（五四学制）（2024）八年级上册3 三角形的中位线优秀课件ppt，共38页。PPT课件主要包含了平行四边形的判定，对角线，回顾与思考，探究思考，知识点，三角形中位线的性质，DE和边BC关系，数量关系，位置关系，DEBC等内容，欢迎下载使用。

三角形中位线的性质三角形中位线在四边形中的应用
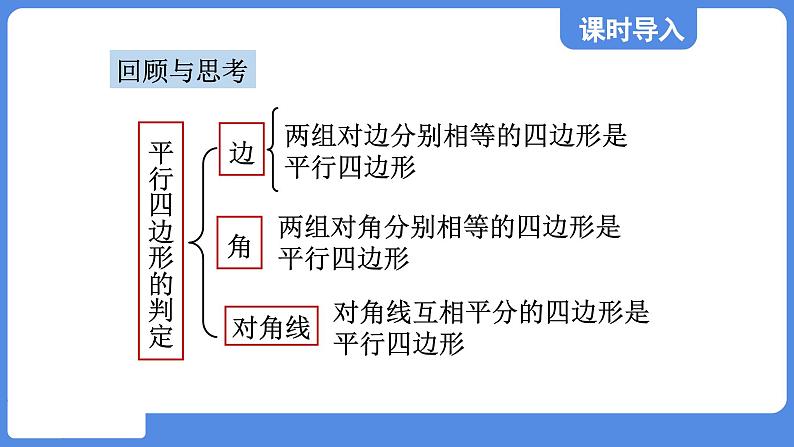
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
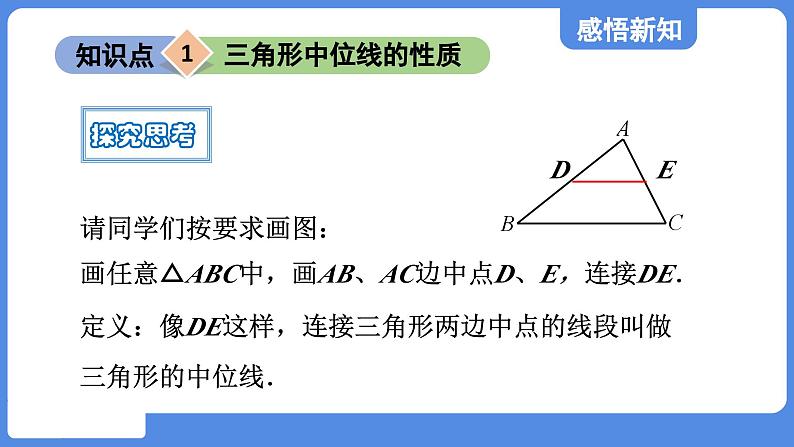
请同学们按要求画图：画任意△ABC中，画AB、AC边中点D、E，连接DE．
定义：像DE这样，连接三角形两边中点的线段叫做三角形的中位线．
1. 一个三角形有三条中位线.2. 三条中位线将原三角形分割成四个全等的三角形，三个面积相等的平行四边形.3.三角形的中位线与三角形的中线的区别：三角形的中线是连接一顶点和它的对边中点的线段，而三角形的中位线则是连接两边中点的线段.4.三角形的一条中位线与第三边上的中线互相平分.
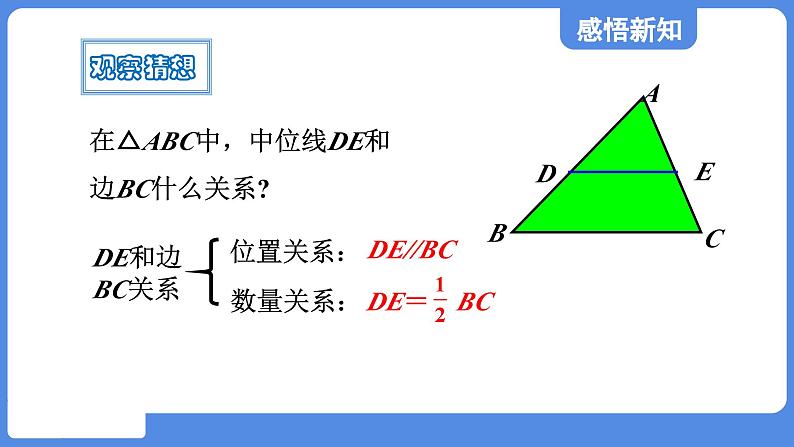
在△ABC中，中位线DE和边BC什么关系?
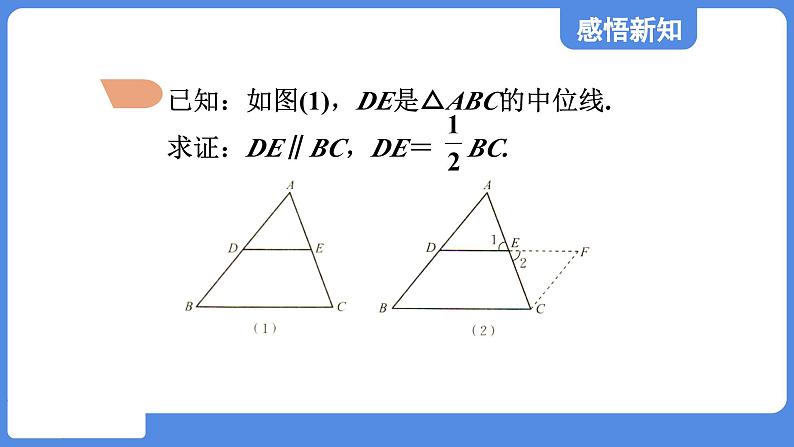
已知：如图(1)，DE是△ABC的中位线.求证：DE∥BC，DE＝ BC.
如图(2)，延长DE到F，使FE＝DE，连接CF.在△ADE和△CFE中，∵AE＝CE，∠1＝∠2，DE＝FE,∴△ADE≌△CFE.∴∠A＝∠ECF，AD＝CF.
∴CF∥AB.∵BD＝AD， ∴CF＝BD.∴四边形DBCF是平行四边形(一组对边平行且相等的四边形是平行四边形).∴ DF∥BC(平行四边形的定义)，DF＝BC(平行四边形的对边相等).∴DE∥BC，DE＝ BC.
利用三角形中位线定理可以证明小明分割的四个小三角形全等.
如图，已知E为平行四边形ABCD中DC边延长线上一点，且CE＝DC，连接AE，分别交BC，BD于点F，G，连接AC交BD于点O，连接OF.求证：AB＝2OF.
点O是平行四边形两条对角线的交点，所以点O是线段AC的中点，要证明AB＝2OF，我们只需证明点F是线段BC的中点，即证明OF是△ABC的中位线．
∵四边形ABCD为平行四边形，∴AB∥CD，AB＝CD.∵E为平行四边形ABCD中DC边延长线上一点，且CE＝DC， ∴AB∥CE，AB＝CE.∴四边形ABEC是平行四边形．∴点F是BC的中点． 又∵点O是AC的中点，∴OF是△ABC的中位线． ∴AB＝2OF.
证明线段倍分关系的方法： 由于三角形的中位线等于三角形第三边的一半，因此当需要证明某一线段是另一线段的一半或两倍，且题中出现中点时，常考虑三角形中位线定理．
已知三角形的各边长分别为8 cm，10 cm和12 cm，求以各边中点为顶点的三角形的周长.
以各边中点为顶点的三角形的周长为 (8＋10＋12)＝15(cm)．
如图，A，B两地被池塘隔开，小明通过下面的方法估测出了A，B间的距离：先在AB外选一点C，然后步测出AC，BC的中点M，N，并步测出MN的长，由此他就知道了A，B间的距离. 你能说说其中的道理吗？
由题意可知，MN是△ABC的中位线，所以AB＝2MN.所以测出MN的长，就可知道A，B间的距离．
如图，要测定被池塘隔开的A，B两点的距离，可以在AB外选一点C，连接AC，BC，并分别找出它们的中点D，E，连接ED. 现测得AC＝30 m，BC＝40 m，DE＝24 m，则AB＝(　　)A．50 m B．48 m C．45 m D．35 m
如图，在△ABC中，AB＝3，BC＝4，AC＝2，D，E，F分别为AB，BC，AC的中点，连接DF，FE，则四边形DBEF的周长是(　　)A．5 B．7 C．9 D．11
如图，△ABC的面积是12，点D，E，F，G分别是BC，AD，BE，CE的中点，则△AFG的面积是(　　)A．4.5 B．5 C．5.5 D．6
如图，在△ABC中，AB＝AC，E，F分别是BC，AC的中点，以AC为斜边作Rt△ADC，若∠CAD＝∠CAB＝45°，则下列结论不正确的是(　　)A．∠ECD＝112.5° B．DE平分∠FDCC．∠DEC＝30° D．AB＝ CD
议一议如图，任意画一个四边形，以四边的中点为顶点组成一个新四边形，这个新四边形的形状有什么特征？请证明你的结论，并与同伴交流.
三角形中位线在四边形中的应用
中点四边形的定义：依次连接任意四边形各边中点所得到的四边形称为中点四边形．拓展：不管四边形的形状怎样改变，中点四边形始终是平行四边形．
如图，在四边形ABCD中，点E，F，G，H分别是边AB，BC，CD，DA的中点，连接EF，FG，GH，HE，得到四边形EFGH，求证：四边形EFGH是平行四边形．
如图，连接BD.∵点E，H分别是边AB，DA的中点，∴EH为△ABD的中位线．∴EH∥BD，EH＝ BD.同理可得：FG∥BD，FG＝ BD.∴EH∥FG，EH＝FG.∴四边形EFGH是平行四边形．
1. 依次连接四边形各边中点所得到的四边形叫中点四边形，所有的中点四边形都是平行四边形.2. 利用中位线定理判定平行四边形，一般用“一组对边平行且相等”的方法.
此题主要考查了平行四边形的判定及三角形中位线定理等知识，熟练掌握三角形中位线定理是解题的关键．
如图，已知E，F，G，H分别为四边形ABCD各边的中点，若AC＝10 cm，BD＝12 cm，则四边形EFGH的周长为(　　)A．10 cm B．11 cm C．12 cm D．22 cm
如图，已知长方形ABCD中，R，P分别是DC，BC上的点，E，F分别是AP，RP的中点，当P在BC上从B向C移动而R不动时，下列结论成立的是(　　)A．线段EF的长逐渐增大B．线段EF的长逐渐减小C．线段EF的长不改变D．线段EF的长先增大后减小
如图，在▱ABCD中，对角线AC，BD相交于点O，点E是AB的中点，OE＝5 cm，则AD的长为______cm.
如图，四边形ABCD中，∠A＝90°，AB＝3 ，AD＝3，点M，N分别为线段BC，AB上的动点(含端点，但点M不与点B重合)，点E，F分别为DM，MN的中点，则EF长度的最大值为________．
练点1 三角形的中位线及定理
1. 如图，在△ ABC 中，若 AD ＝ BD ， BE ＝ CE ，则下列线 段是△ ABC 的中位线的是(　A　)
2. [母题·教材P139随堂练习T2]如图， A ， B 两点被池塘隔 开， A ， B ， C 三点不共线.设 AC ， BC 的中点分别为 M ， N . 若 MN ＝3 m，则 AB ＝(　B　)
3. 如图，在四边形 ABCD 中，点 E ， F ， G 分别是边 AB ， AD ， DC 的中点，则是图中某个三角形的中位线的线段 是(　D　)
三角形的中位线平行于三角形的第三边，且等于第三边的一半．几何语言(如图)：∵DE是△ABC的中位线，∴DE∥BC．DE= BC．
如图，▱ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点，若AC＋BD＝24 cm，△OAB的周长是18 cm，则EF＝________cm.
易错点：忽视整体思想的应用而求不出中位线的长
点拨：∵AC＋BD＝24 cm，∴OA＋OB＝12 cm，又∵△OAB的周长是18 cm，∴OA＋OB＋AB＝18 cm，∴AB＝6 cm.又∵点E，F分别是线段AO，BO的中点，
∴EF＝ AB＝3 cm.此题易错之处在于忽视运用整体思想求OA，OB的长度和，从而导致求不出中位线长．